【岐阜県公立高校入試】数学　方程式　出題傾向　過去35年

　岐阜県公立高校入試では、毎年必ず「方程式」分野が出題されています。

　「方程式」に関わる問題では、解を求める計算問題、関数（比例、反比例、一次関数、二次関数）の問題での活用などもありますが、「方程式」分野単独での文章題がどのように出題されてきたのかを分析してみます。

　今回は、平成元年度（1989年）から令和5年度（2023年）までの35年分を対象とします。

1　平成元年度（1989年）～平成8年度（1996年）

・平成元年度（連立方程式）
　空港Aを出発し、空港Bを経由して、空港Cに向かう際の、乗客の乗り降りした人数を連立方程式を立てて求める。

・平成2年度（連立方程式）
　A君とB君が受けた10回分の漢字テストの得点表。平均値、範囲などを利用して、A君の2回目の点、B君の7回目の点を、それぞれ$${x}$$点、$${y}$$点として、連立方程式を立てて求める。

・平成3年度（連立方程式）
　ボールを投げる（3点）か、ける（5点）かして、的に当てるゲーム。あわせて20回おこなう。投げた回数を$${x}$$回、けった回数を$${y}$$回として、連立方程式を立てて求める。

・平成4年度（連立方程式）
　数直線上を移動する点Pについて、右に5移動することをR、左に3移動することをLとして、RとLをあわせて20回行い、点Pが特定の位置にある場合を連立方程式を立てて求める。

・平成5年度（連立方程式）
　動物園の一人当たりの入園料。大人とこども、そして大人と子どもの団体割引（大人とこどもあわせて30人以上）の際の金額が与えられている。（2）では、「大人10人と子ども20人未満」でも、「大人10人、子ども20人」より高くなる場合の人数を求める。（3）では、あわせて43人のグループが一般料金の場合より1000円安くなるときの大人と子どもの人数を連立方程式を立てて求める。

・平成6年度（方程式文章題の出題なし）
　連立方程式の計算問題と2次式の因数分解に関わる問題は出題されたが、方程式分野単独の文章題は出題されなかった。ただし、碁石を並べる規則性の問題で文字式を活用した方程式の利用はあった。

・平成7年度（2次方程式）
　2つの数の積と和が（　ア　）に等しいとき、2次方程式を立式して解く（（　ア　）は5以上の整数）。またそのとき、和と積が等しくなる2つの数から、それぞれ1を引いた数の積を求める。

・平成8年度（連立方程式）
　自然数のなかには、2つの自然数の2乗の差で表すことができる数とできない数がある。例として、

$${7=7×1=(4+3)(4-3)=4^2-3^2}$$
$${8=4×2=(3+1)(3-1)=3^2-1^2}$$　が与えられている。

（1）、（2）で12や15の場合を求めるとき、$${x^2-y^2=(x+y)(x-y)}$$　と考えれば、連立方程式として考えることができる。また、（3）で2桁の自然数で2つの自然数の2乗の差で表すことができない数を2つあげる（たくさんあります）。

　出題のなかった平成6年度、方程式というくくりでもない平成8年度などがあった一方で、その他の年度は連立方程式のよくある問題が出題されており、難易度もかなりやさしい部類だった。

２　平成9年度（1997年）～平成16年度（2004年）

・平成9年度（2次方程式）
　直角二等辺三角形の直角をはさむ2辺（10㎝）に接する長方形の面積があたえられている（20㎠）。長方形の各辺の長さを求めるのに、2次方程式を利用して解いた太郎君の答案に対し、穴埋めと答案の不十分な点を補う出題。また長方形の辺の数値が整数で、面積がもっとも20㎠に近い場合を求める。

・平成10年度（連立方程式）
　バスケットボールのフリースロー記録会の結果が、4月、5月、6月について度数分布表があり、また、4月と6月の相関表がある。
　度数分布票の$${x}$$、$${y}$$、$${z}$$を、$${x}$$は4月の合計からの引き算で求め、$${y}$$、$${z}$$については、5月の平均値を利用して、連立方程式を立てて求める。また、相関表内の$${a}$$～$${e}$$を度数分布票を元にして求める。

・平成11年度（2次方程式）
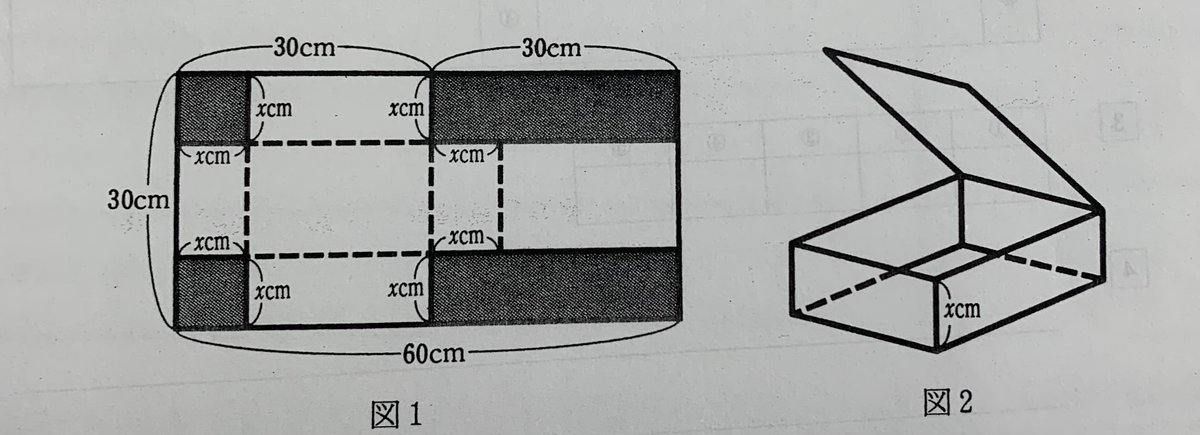
　長方形の厚紙（縦30㎝、横60㎝）の角を切り取って、高さ$${x}$$㎝の直方体を組み立てる。（1）箱の底面が200㎠になるときの$${x}$$の値を2次方程式を立てて求める。（2）箱の深さが3㎝のとき、1辺3㎝の立方体を隙間なく箱に敷き詰めると何個入るか、また、深さが3㎝でない場合の隙間なく詰められる深さ$${x}$$を求める。

・平成12年度（連立方程式）
　自転車に乗って出発し、途中で自転車が故障したため、そこから歩いて目的地に行く問題。自転車に乗った時間を$${x}$$時間、歩いた時間を$${y}$$時間として連立方程式をつくる。そして、自転車に乗った距離を$${x}$$km、歩いた距離を$${y}$$kmとして連立方程式をつくる。
　どちらか一方を選んで式を立てる問題として出題されました。「道のりと速さ」の分野から方程式が出題されるのは昭和63年以来12年ぶりでしたが、関数などでは頻繁に出題されています。

・平成13年度（2次方程式）
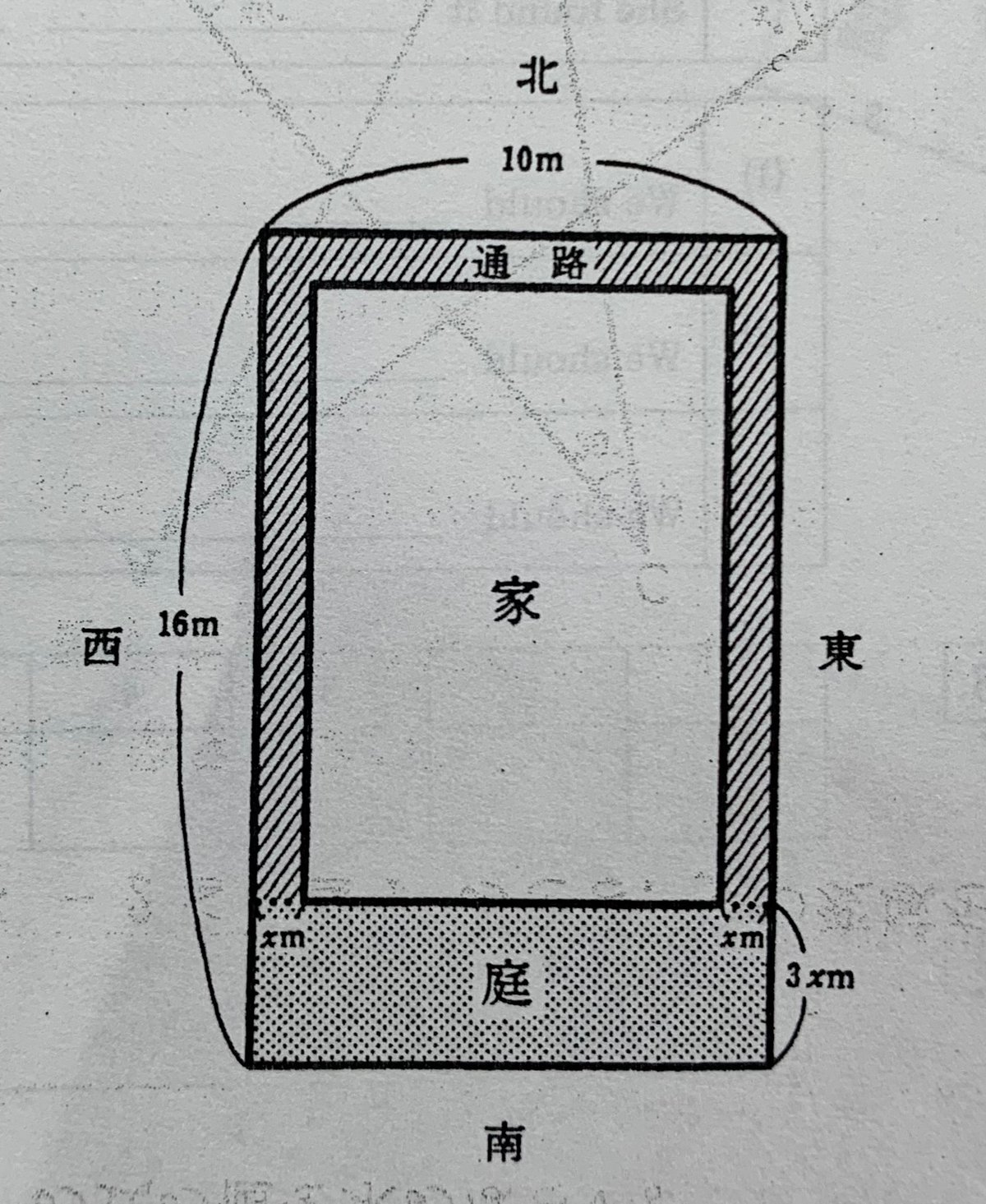
　縦16m、横10mの長方形の土地に家を建てる。通路と庭を確保して家の面積が土地の60％になるようにし、北、東、西の3方向に幅$${x}$$mの通路、南に縦$${3x}$$m、横10mの庭をつくる。家の面積を2次式で表し、2次方程式にして解を求める。式が何を表すのかを言葉で説明させる「ゆとり時代」っぽい出題でした。

・平成14年度（1次方程式）
　3つの容器に水が入っており、1つの容器の水を、他の2つの容器に残さず入れた時、2つの容器に残った水の量が、一方がもう一方の2倍になるようにする。$${x}$$を求めるだけの1次方程式。

・平成15年度（2次方程式、1次方程式）
　1辺が6㎝の正方形の紙を4枚張り合わせて、面積が100㎠をつくる。
　のりしろを$${x}$$㎝として、2次方程式および1次方程式をつくって幅を求める。

・平成16年度（連立方程式、1次方程式）
　銅を90％含む合金と、銅を50％含む合金があり、これを溶かして混ぜ、銅を60％含む合金を100gつくる。連立方程式、1次方程式の両方をつくり、それぞれ何g必要かを求める。

　平成14年度から明らかに傾向が変わった。これは、この年度から「特色化選抜入試」が始まったことに関係している。定員の20％までを「高校独自問題」で選抜できる入試で、ほぼ全高校が参加したが、実質は難関校の青田買いとそれ以外の高校の推薦入試の代替程度の意味しかなかった。
　1次方程式単独の出題は、それまで20年近くなく、連立方程式や2次方程式で解く問題を、あえて1次方程式にして解く問題も出題されるなど、かなり工夫の見られる出題だった。

３　平成17年度（2005年）～平成24年度（2012年）

・平成17年度（2次方程式）
　長方形の土地に幅$${x}$$mの通路をつくる問題。2次方程式を立てて解く。

・平成18年度（連立方程式）
　全長3600mのコースを、途中の地点Pまでと、地点Pからで速さを切り替えて20分で走る問題。（1）道のりをそれぞれ$${x}$$m、$${y}$$mにして、連立方程式を立てて解く。（2）もう一人は、前半を同じ速さ、後半を違う速さで走って22分かかった。後半の速さを求める。

・平成19年度（2次方程式）
　1辺14mの正方形の花壇の角に4つの合同な直角三角形の土地を区切って赤い花を植え、内部の四角形には黄色い花を植える。2通りの2次方程式を立てて、直角三角形の短い方の辺の長さを求める。

・平成20年度（連立方程式、1次方程式）
　小中学生の活動参加人数の問題。参加者合計は昨年も今年も180人で、小学生は10％減、中学生は20％増。連立方程式と1次方程式をそれぞれ立てて、人数を求める。

・平成21年度（2次方程式）
　周の長さが48ｍのＬ字型の区画をつくる。面積が80㎠になるように2次方程式を2通り立てて求める。また、区画内での動物の移動範囲を求める問題もあった。

・平成22年度（連立方程式）　
　1周1000mの池の周りを2人で同じ方向に走る問題。2人の速さはあたえられており、連立方程式を、道のりと時間の両方で2通り立てて求める。

　この年度は、関数や規則性の問題でやられた受験生が多かった。この年度より、特色化選抜入試が定員の50％となり、一般選抜入試は敗者復活戦の様相となった。

・平成23年度（2次方程式）
　車の空走距離と制動距離の問題。問題集などにもよく掲載されている有名問題で、前半が速さに比例、後半が速さの2乗に比例するため、移動距離から2次方程式で速さが求められる。

・平成24年度（連立方程式、2元1次方程式）
　りんごとみかんをそれぞれ何個か買い、代金がともに1080円になった。りんごとみかんの代金をそれぞれ連立方程式を立てて求める。
　また、それ以外に1080円になる個数の組み合わせを答える。解答が複数通りある2元1次方程式の出題は30年近くなかった。

　複数通りの考え方で式を立てさせる、「太郎さん、花子さん」問題の出題が目立った。大学入試共通テストで問われているような形式だが、解き方を強制される点は優秀な生徒にはストレスだっただろう。平成19年度から3年間は、特色化選抜入試の学校独自問題が廃止されて、全県共通問題となった（定員20％）。また、平成22年度から24年度までの3年間は定員が50％まで広げられた。しかし、私立入試の日程前倒し、3学期の授業が成り立たないなど、弊害が多発し、事実上、「失敗」という評価で特色化選抜入試の幕は閉じた。

４　平成25年度（2013年）～平成31年度（2019年）

・平成25年度（連立方程式）
　114Lの空の水槽に、6Lの容器Aと4Lの容器Bを用いて、池から水をくむ問題。容器Aでは、池までの1往復に48秒、容器Bでは1往復に36秒かかる。
（1）はじめ容器Aで何回か水を汲み、のちに容器Bを使って水を汲んだ場合に15分48秒で満水になった。時間と水の量で連立方程式を立てて解く。
（2）容器Aと容器Bを同時に使った場合、満水になる時間を求める。

・平成26年度（2次方程式）
　秒速35ｍでボールを打ち上げた際に、$${x}$$秒後のボールの高さは、$${35x-5x^2}$$mで与えられている。
（2）では、秒速5mの一定の速さで打ち上げた風船Bを、9秒後にボールAを秒速35mで打ち上げた際に、ボールAが風船Bにあたった高さを2次方程式を立てて求める。

　数学の教科書にも類題が掲載されており、見た目ほどごつくない。

・平成27年度（連立方程式、1次方程式）
　ペットボトルキャップ集めの活動に関して、A地域とB地域で合わせて80人、また、各地域の集めた平均個数が与えられている。連立方程式と1次方程式の2通りの方程式を立てて、それぞれの地域の人数を求める。
　（3）では、アルミ缶を集める問題があるが、（2）で生徒の人数が正しく出ていないと解けない。平均個数と、個数の差が与えられているので、1次方程式を立てて解き、合計個数を求める。

・平成28年度（2次方程式※）
※　$${x^2+ax-b=0}$$について、与えられた条件にあわせて問題を解く。純粋な計算問題で、文章題ではない。

・平成29年度（1次方程式、2元1次方程式）
　食塩水の問題。
（1）濃度5％の食塩水A 400gに含まれる食塩の量。
（2）食塩水A 400gに100gの水を加えて食塩水Bを作ったときの、食塩水Bの濃度。
（3）500gの食塩水Bに、濃度9％の食塩水Cを混ぜて、濃度5％にしたい。食塩水Cの量はいくらか。
　単純な1次方程式、というよりも、1年生理科で学習する内容。
　また、この年度は最終問題で解が複数ある2元1次方程式を立てて解く問題が出題されている（誕生日から数をつくる手順に沿って方程式を立てる）。

・平成30年度（1次方程式）
　1個120円で売ると1日で240個売れる商品があり、1円値下げするごとに1日あたり4個多く売れる。値下げ額を$${x}$$円と考えて1次方程式を立てて解く。

・平成31年度（連立方程式、2元1次方程式）
　1時間あたりで、機械AでQをつくると、Pをつくるときの2割増しの個数、機械BでQをつくると、Pをつくるときの1割減。また、機械Aと機械BでPだけをつくると55個/時、Qだけをつくると57個/時である。
　連立方程式を立てて、A、Bがそれぞれ1時間でP、Qを何個作れるかを求める。
（2）では、A、Bをそれぞれ複数台使って、Qだけを1時間に600個作っているときのA、Bそれぞれの台数を求める。（1）で正しい答えが出ていないと2元1次方程式を立てられない。

　平成の終わり近くになると、それまでの文章をしっかり読んで立式する問題から単純な計算問題、基本の方程式問題、代入するだけで解く問題など平易な出題が続いた。一方で、2元1次方程式で複数通りの買いを求めさせる問題が何度か出題されており、この時期の特徴といえる。

５　令和2年度（2020年）～令和5年度（2023年）

・令和2年度（2次方程式）
　カレンダーの隣接する3つの数字に関する問題。最小の数と2番の数は上下に、2番目の数と最大の数は左右に隣接している。最小の数と2番目の数のそれぞれの2乗の和は最大の数の2乗に等しい。
　三平方の定理ででてくる「ピタゴラス数」を知っていると方程式を立てるまでもなく答えはわかるが、ここでは$${x^2+ax+b=0}$$の形で2次方程式を立てる問題となっている。

・令和3年度（出題無し）
　この年度では、2⃣～4⃣の大問3つのすべてが関数の問題として出題され、純粋な方程式の出題はなかった。6⃣は文字式の出題。

・令和4年度（2次方程式※）
　平成28年度と近い、純粋な計算問題。文章題の出題はなかった。
　$${x^2+ax-8=0}$$について解く問題だが、1⃣の小問集合で出題されるレベル。

・令和5年度（2次方程式）
　2つの直方体の容器に水を入れて移す。容器Aの底面は、周の長さが20cmの正方形、容器Bの底面は、周の長さが20cmの長方形で、高さは40cm
　容器Ｂの底面の短い方の辺の長さを$${x}$$として、まずは底面の面積を式で表し、次の問題で、容器Ｂを満水にして容器Ａに移すと高さが30ｃｍになったことから$${x}$$を求める。
　式は、$${40x(10-x)=750}$$となり、整理すると$${4x^2-40x+75=0}$$となる。$${(2x-5)(2x-15)=0}$$と因数分解することも可能だが、解の公式を使う場合は、根号が外れて、±が計算できることに注意。
　答えは、短い方の辺の長さ

　令和に入り、方程式単独の文章題への比重がやや低くなっている。これはコロナ禍による学習不足への配慮も関係しているだろう。この数年は「例外」と考え、方程式文章題の学習を軽視してはいけない。

　以上、岐阜県公立高校入試数学35年分の方程式を振り返ってみた。近年はともかくとして、バリエーションにとんだ出題がされていた時期もあり、遡って学習する価値があるだろう。もちろん、関数分野との関係は密接であり、方程式「だけ」を学習するのではなく、関数と並行して学習することをおすすめする。