仮想(電験二種理論H25問2)
世の中欲望に満ち溢れている
Chapter2 電磁気の問題


答えの選択肢は予測が付くのになかなか至れなかった問題。
解いていく。
⑴について。
NI=HLの基本式で考えた為悩んだが、こいつは磁気回路の考え方で良いことに気づく。
条件を書いて磁気抵抗を求める。

オームの法則でφを求めるのと磁束密度の公式を書く。
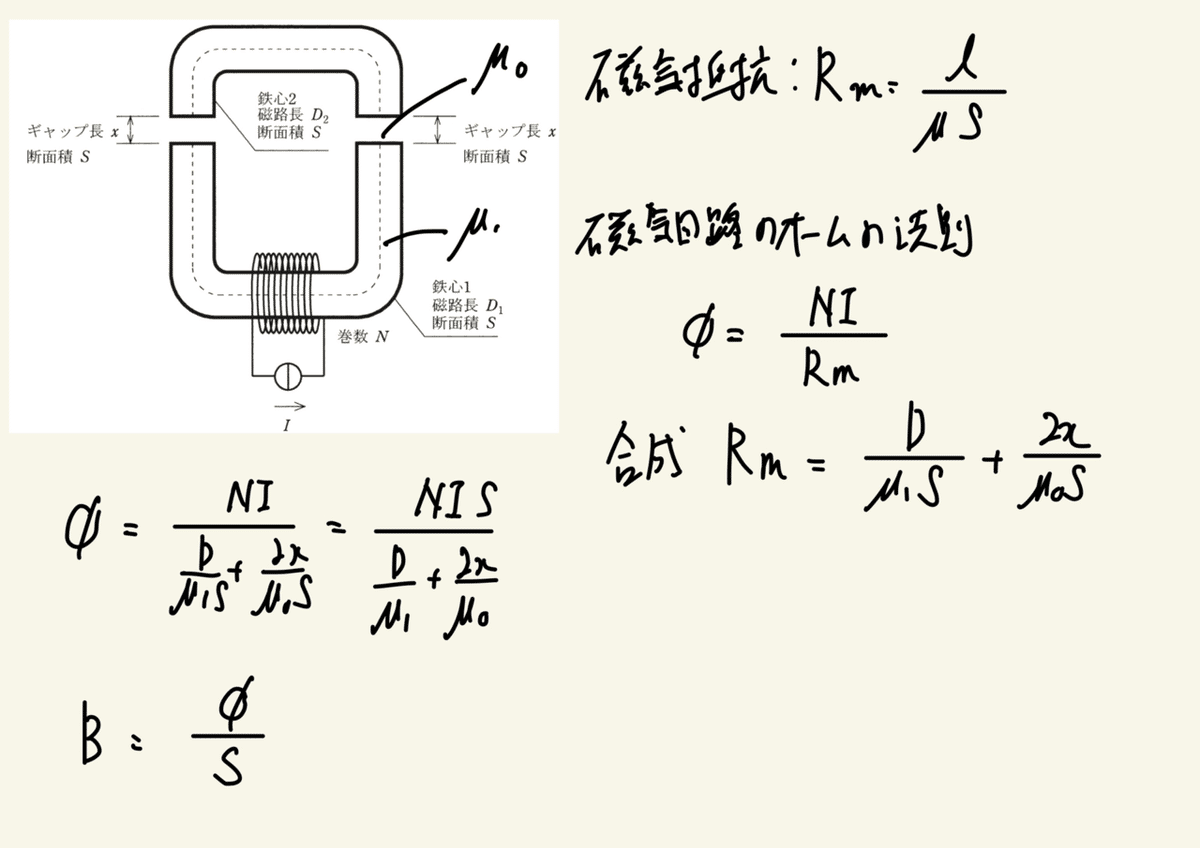
後は代入して文字を消せば

モヤモヤしながら考えていたのでスッキリした。
⑴の答えは(ロ)となる。
⑵について。
インダクタンスの式を書くと

上記となり先ほどのφが使えるので代入していく。

先ほどのBでないことに注意。
よって⑵の答えは(リ)となる。
⑶について。
磁気エネルギーの公式は下記となる。

Lを用いて表すのでこれが答えにもなる。
よって⑶の答えは(チ)となる。
⑷について。
仮想変位ってなんだ?
ここはもう解説を読む。
仮想変位において、吸引力はF=-dW/dxの関係がある。
????????
とりあえず式を書いてみるか…

微分という単元をちゃんとやらなきゃいけない気がしてきたな…
なんとかと置いたあとのdがなんとなくしかわからん。
言語化できないって奴だな、そのせいで脳が処理しきれてない。
とりあえず計算過程を書いてみる。

まあこれは仮想変位がわかってからの計算だがこんなもんかな。
とりあえずFの式に関しては仮想変位であるときこういった関係があるというのを覚えておく。
⑷の答えは(ト)となる。
⑸について。
条件より以下のように式変形ができる。

この式から選択肢を選ぶと「電流Iの2乗に比例し、ギャップ長xの2乗に反比例する」となることがわかる。
よって⑸の答えは(ヨ)となる。
あとがき
寝る前ヨガの効果はそれなりだった。
当直で試して明けの今日それなりに動けている。
無限に体力を回復させてくれないかしら…w
ではでは。