数Ⅲで匙投げた結果(電験二種理論H23問1)
積分?あー積分ね、うんうん。
問1 電磁気の問題


はじめ分母二乗の積分がわからなくて困っていた。しかしそもそもそんな式はなかったという…
あ、でもlogの積分は予想で答えてます。
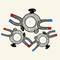
⑴について。
ガウスの法則(円筒導体編)より公式は

今までも何度か出てきた公式、点電荷の時と違うことに注意する。
今回それで一度ハマってしまい、解くのにそこそこの時間を要した。まあ本番では一度飛ばして戻ってくるから時間の浪費はしないとは思うが・・・
余談はさておき、⑴の答えは(ト)となる。
⑵について。
問題文にある通り⑴の答えを積分して電位差を導出する。

導出したいのはq=の形なので上式を変形すると
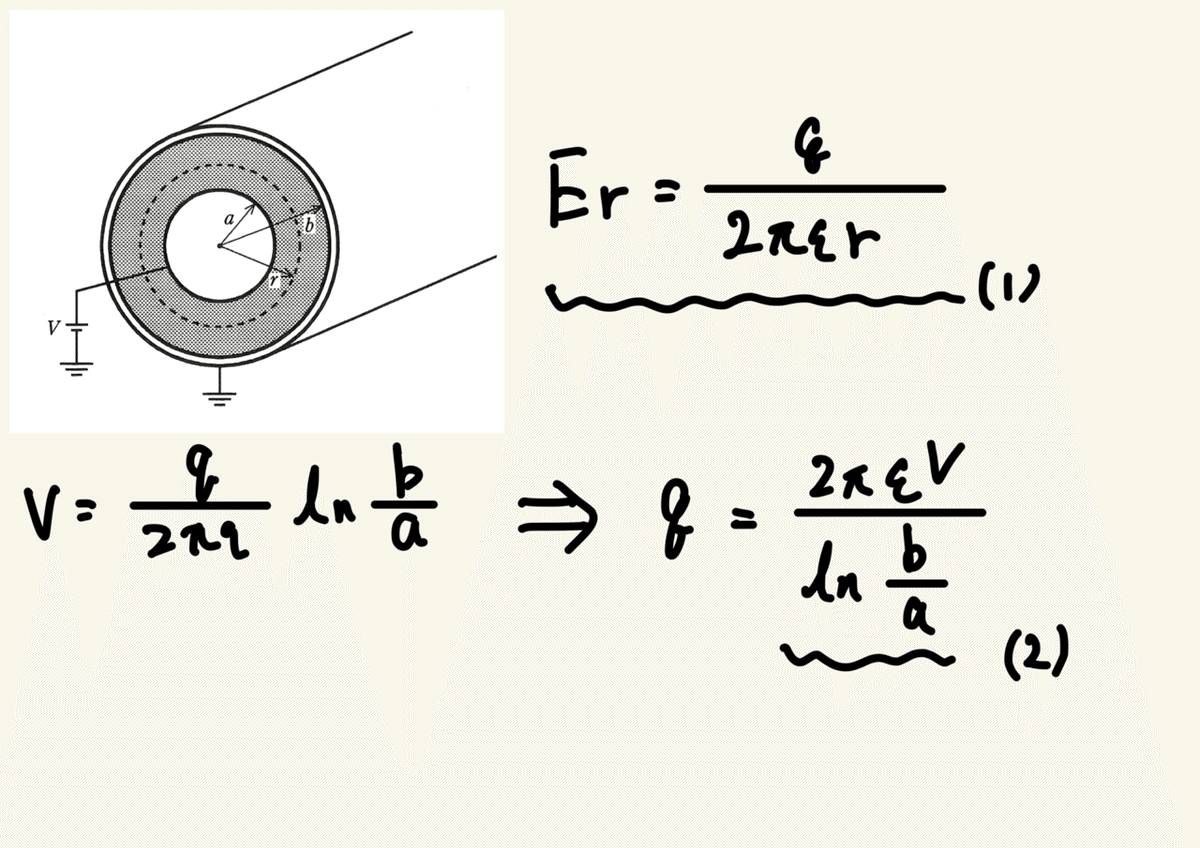
上記のような式を導き出せて⑵の答えは(ル)となる。
⑶について。
電界の強さは距離に反比例しているので内部導体がはじまる地点、距離aの時が最大である。
Eマックスとして代入すると

①及び②式からとあるのでqも代入する。

⑶の答えは(ワ)となる。
⑷について。
⑶の答えを微分すると言われてもなあ・・・と悩んだ。
答えの形は想像つくが過程がはっきりとはわからない、予想だと
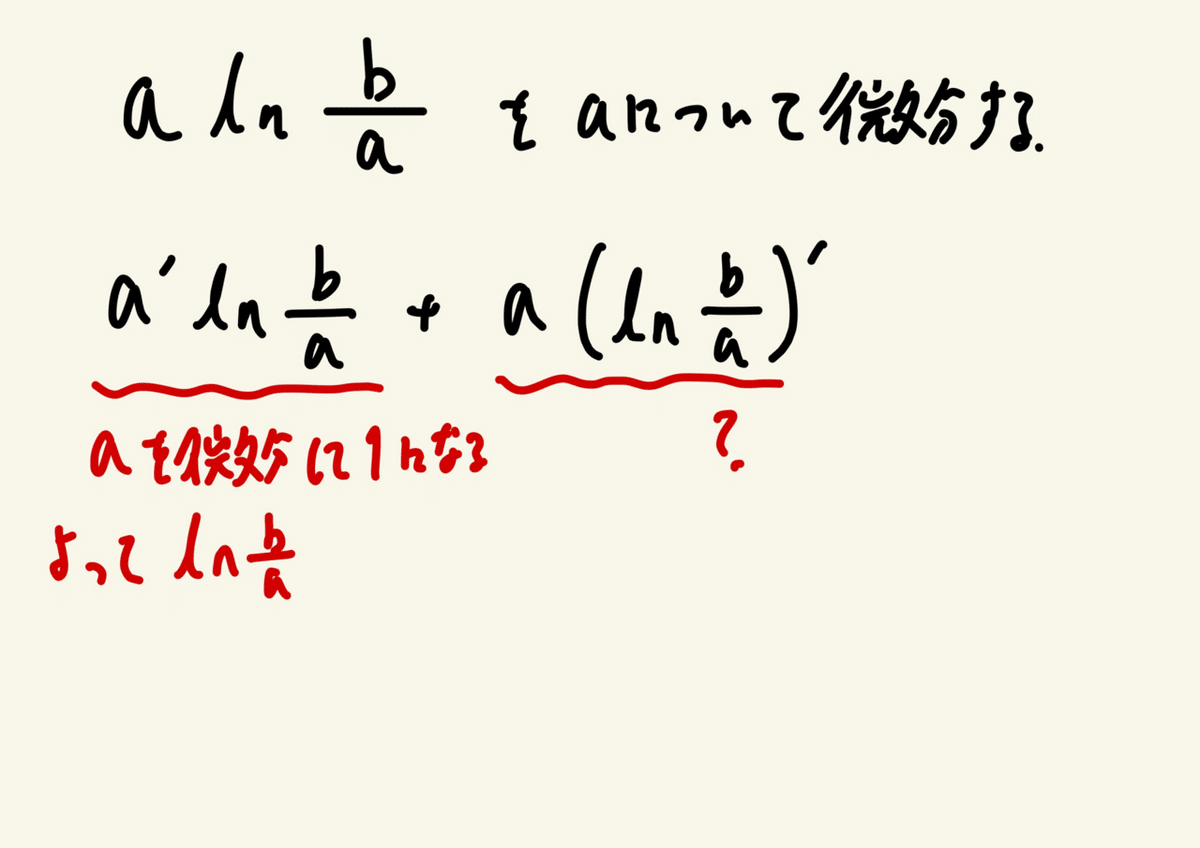
こんな感じだと思っているので答え候補の(へ)と見比べる。
後半が−1となっているのでどうしたらこうなるのか考える。

なんとなくわかってきたので残りの部分を計算してみる。
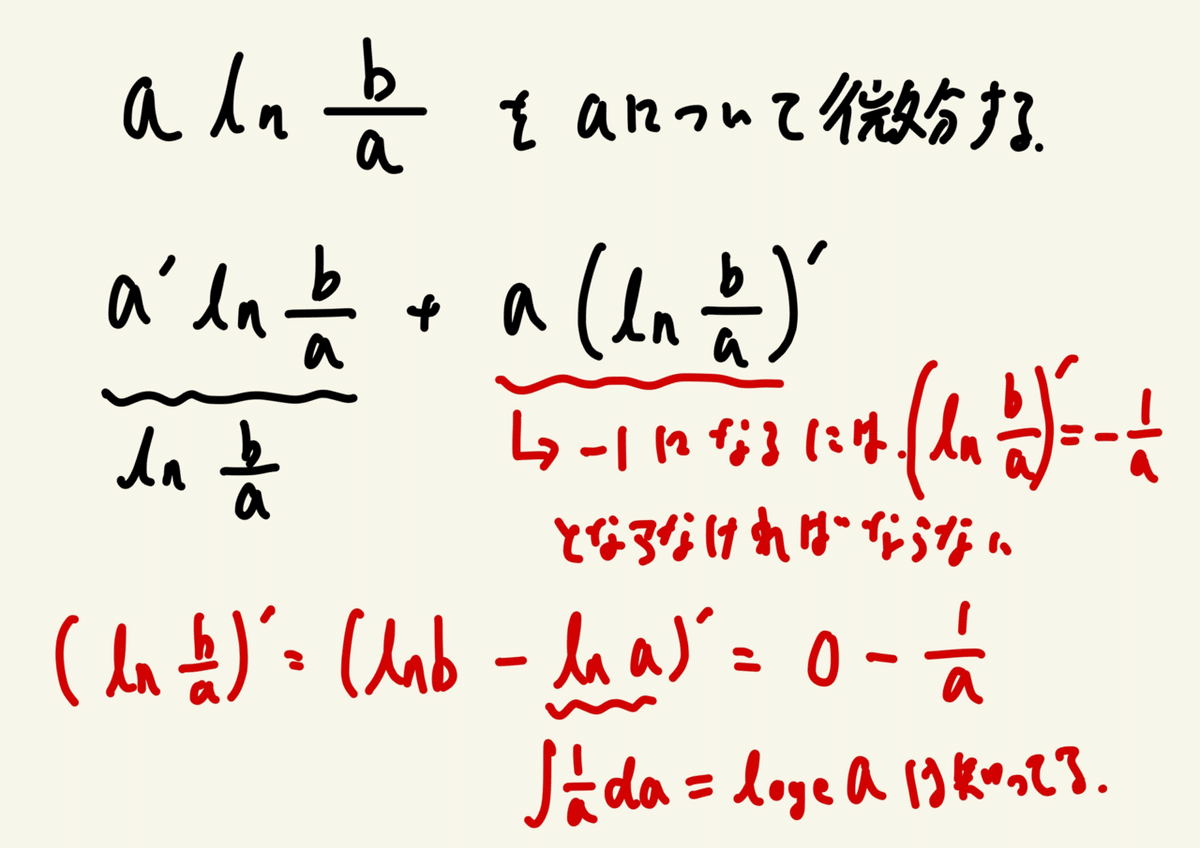
積分してlogになるのは微分方程式で散々やってるから覚えている。
微分したらその逆になるのは当たり前か笑
意外とそういった発想は解いてる最中には出ないものである。
以上をまとめると
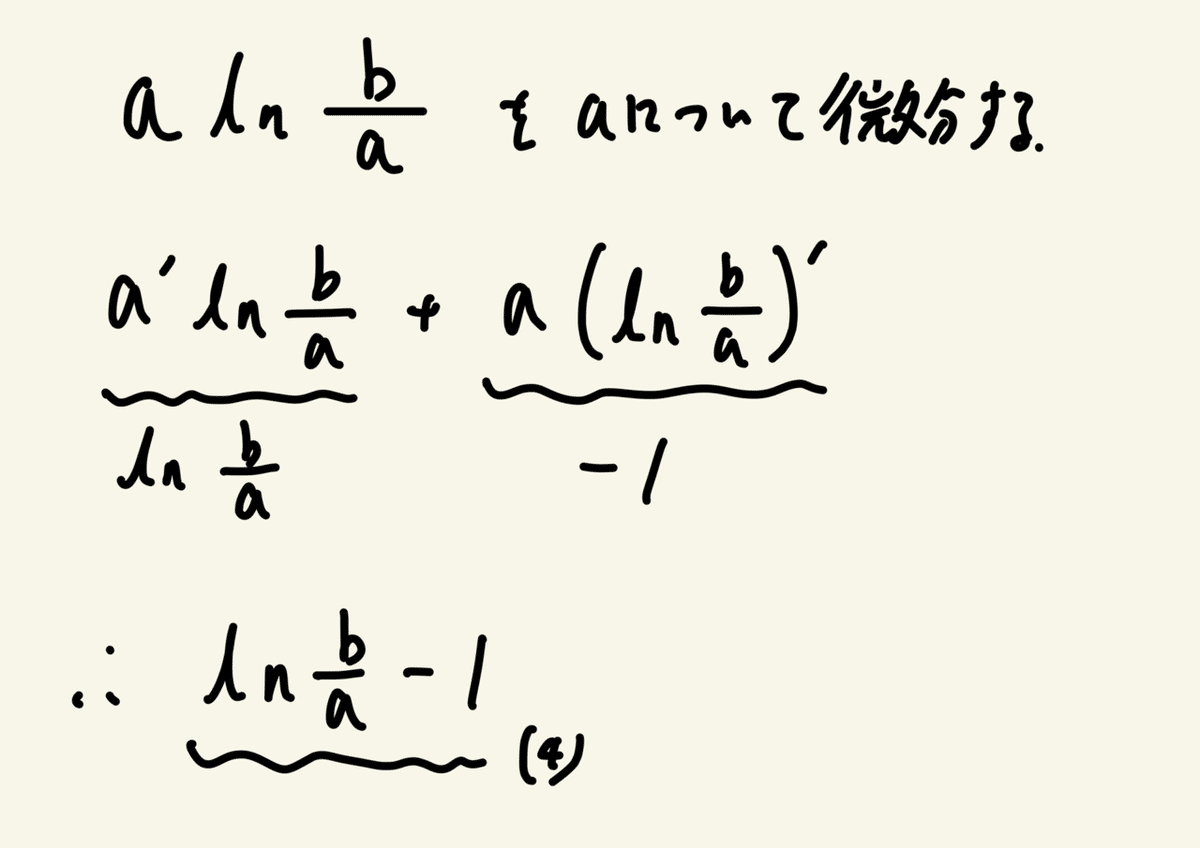
⑷の答えは(へ)となる。
⑸について。
⑷の式が0となるaを求めるので計算すると
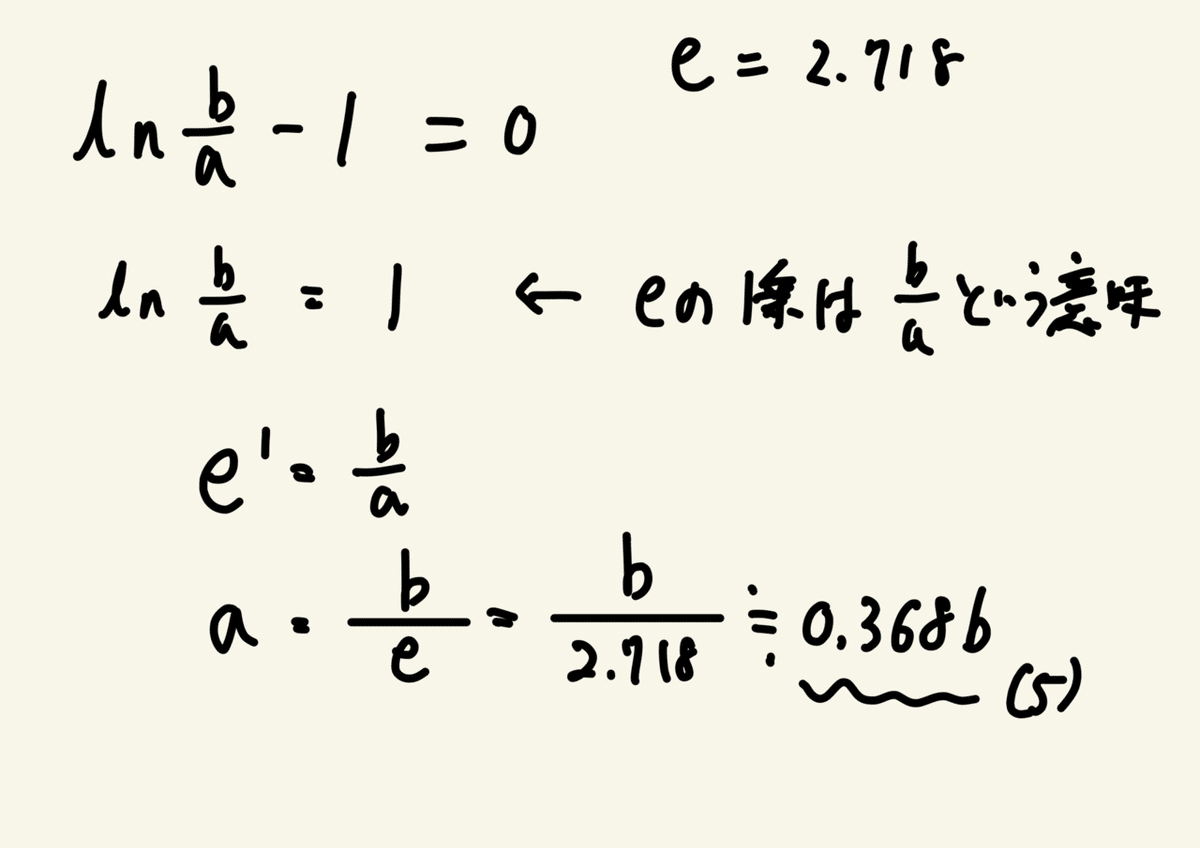
昔、きっちり数字が出ない答えは苦手だったがもう慣れたもんだ。
⑸の答えは(ニ)となる。
あとがき
とてもおサボりしてしまったのでまたキョウカラガンバリマス。
気を引き締めないと勉強が間に合っても記事書けないと思うしなぁ笑
日々続けるのが難しいのよ。
ガンバリマス。
デハデハ。