ノートンはテブナンに似ている(電験二種理論H23問5)

ノートンの式はーテブナンに似ているー
この式なら問題を終わらせることができる

問5 ノートンの定理で直流回路の問題

ノートンの定理ってなんだっけってなったが問題文が丁寧なのでまあわかりやすいかな？

⑴、⑵について。

図1(b)を短絡させて回路について考えたい。
なのでまず短絡させて合成抵抗を求めて全体の電圧を導出するところまでやってみる。

全体の電圧が導出できたので各箇所の電圧降下を考える。
短絡した地点より上側が12/7［Ω］、下側が10/7［Ω］で7［A］の電流と考えると電圧は以下のように書き込める。

各箇所の電圧降下がわかったので抵抗を使い、電流を求める。

解説だとキルヒホッフの法則よりとか書かれているが回路に書き込んでみれば各箇所に流れる電流はわかると思う。
上記の図より⑴の答えは(ワ)、⑵の答えは(ニ)となる。

⑶について。
電圧源は短絡、電流源は開放。
以上、⑶の答えは(ル)。

⑷について。
回路を書き換えるとわかりやすい。

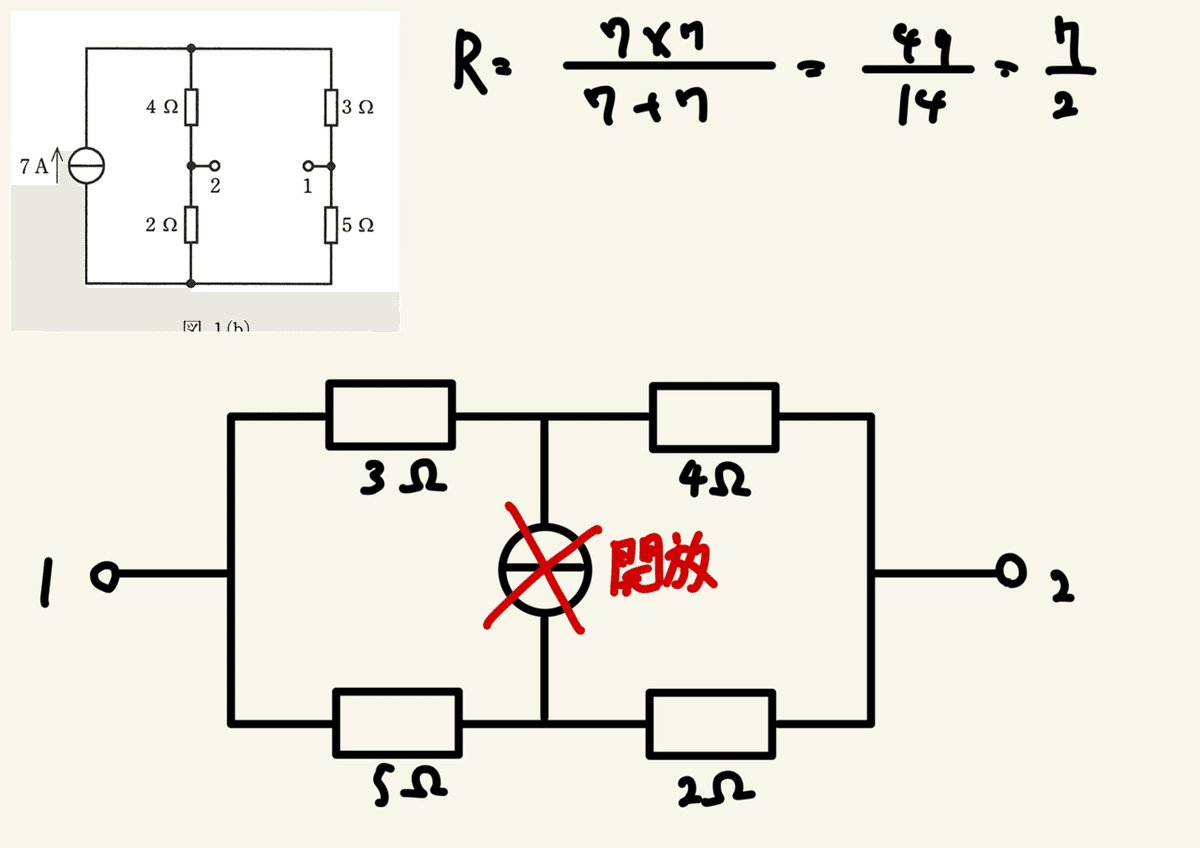
合成抵抗まで求めた。
注意だがまだコンダクタンスは求めていない。
私が問題作成者なら7/2を選択肢に入れたくなる、この時は優しかったのかその選択肢はない。
余談はさておきコンダクタンスを求める。

よって⑷の答えは(イ)となる。

⑸について。
いきなりノートンの定理と言われるとパッとは書けない。
テブナンの定理に似ているというのはわかったのでまずそっちを書いてみる。

テブナンがこの形ならノートンはこんな形だろうと予想できる。

つい答えまで進んでしまったがこんな感じだろう。
テブナンの定理とノートンの定理は対のイメージで覚えると楽な気がする。
以上より⑸の答えは(ト)となる。

あとがき

久しぶり1日2問投稿ではないだろうか。
5月から本気出す準備はしているので投稿頻度はもっと上がるとは思います。

自分の解き方メモみたいになってる気がしますがまあそれでもいいかなと。
考え方のヒントにでもなれば幸いです。

ではでは〜