制御はTA(電験二種機械制御R4問4)
ここまで予想得点は75点。
ボーダー180点中108点。
一問30点で残り一問で必要点数33点、絶望。
まあそもそも電力管理で平均点超えてないとアウトだけどね。


師匠からの教えにあった通り、試験開始即20分以内にほぼ片付けた。
⑸は難しくてできなかったなぁ。
ではいつも通り丁寧に。
⑴について。
特製方程式とはなにか。
それにはまずRからYへの伝達関数を求める必要がある。

箱を一つにまとめて

伝達関数がもとまった。
では特性方程式とは何か。

赤丸部分を=0としたものが特性方程式である。
整理すると
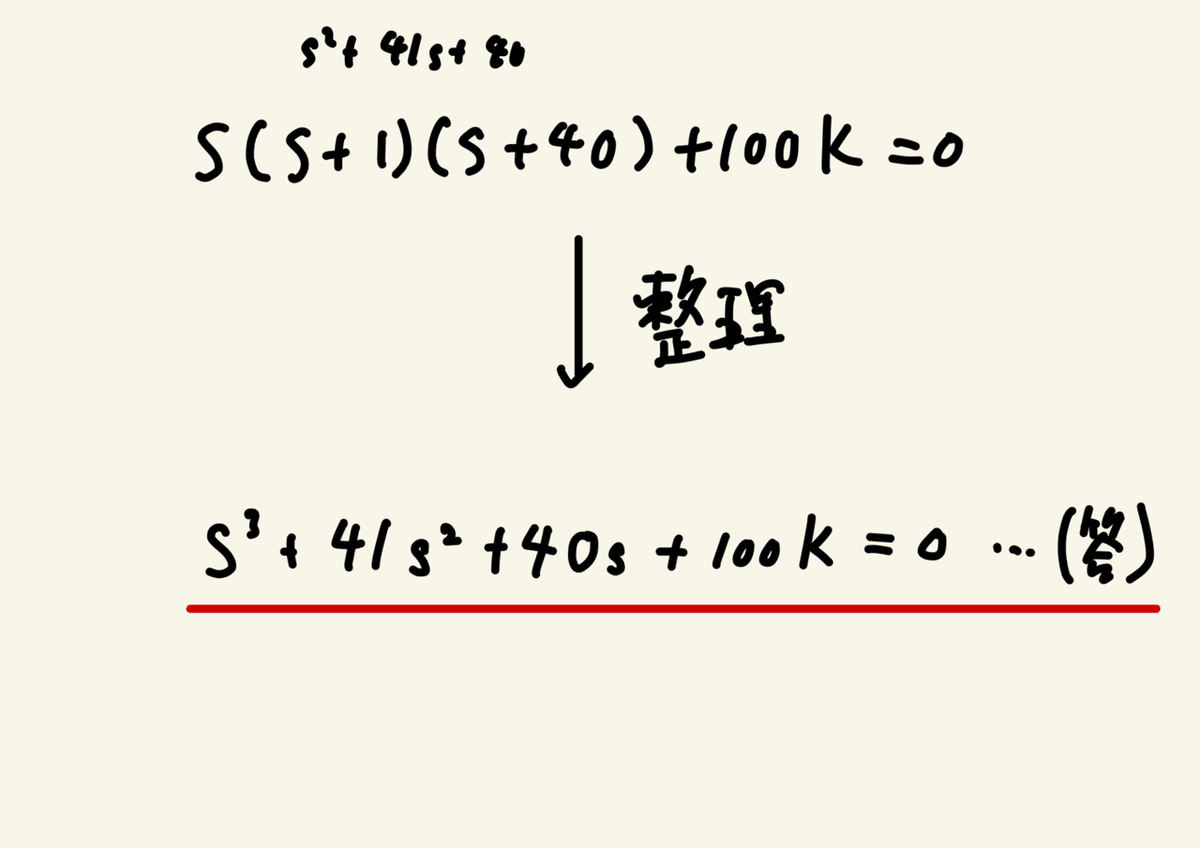
乗数表現が文章だとしにくいので答えは書き込んでおいた。
この式は⑵でも使うので間違えないよう注意。
⑵について。
ラウスの安定判別法を使用するのだがそれにはラウス表を作らねばならない。
ラウス表とは

⑴の特性方程式を当てはめていくと
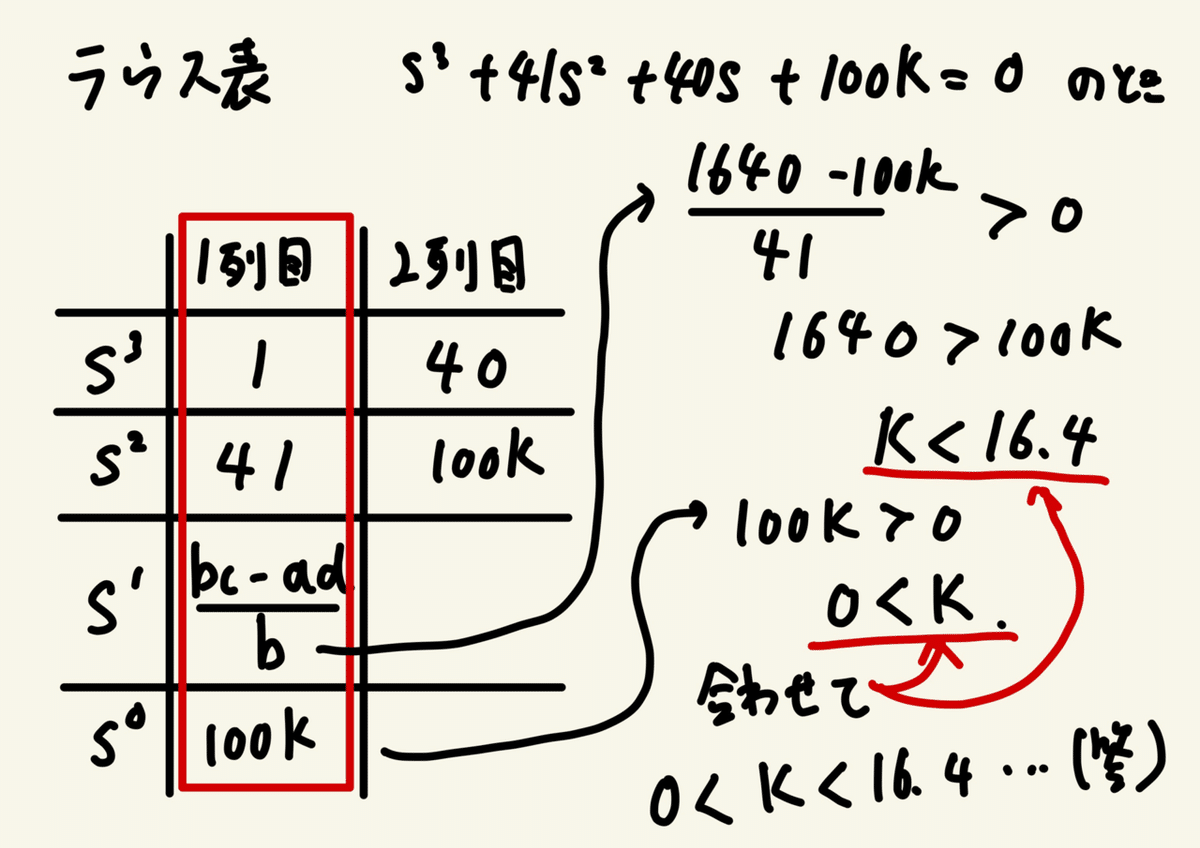
よって答えは0<K<16.4となる。
⑶について。
RかEまでの伝達関数をもとめたいので最初の図の方へ戻る。
Eを式で表すと

あとはYを代入して整理すればよい。

公式解答だとこのあとの都合上分母分子両方因数分解してあったがこれでもいいだろう。
⑷について。
なかなか覚えられなかったラプラス変換、間が空くとやっぱ忘れてる(笑)
まず傾き2のランプ関数を書く、そしてラプラス変換する。
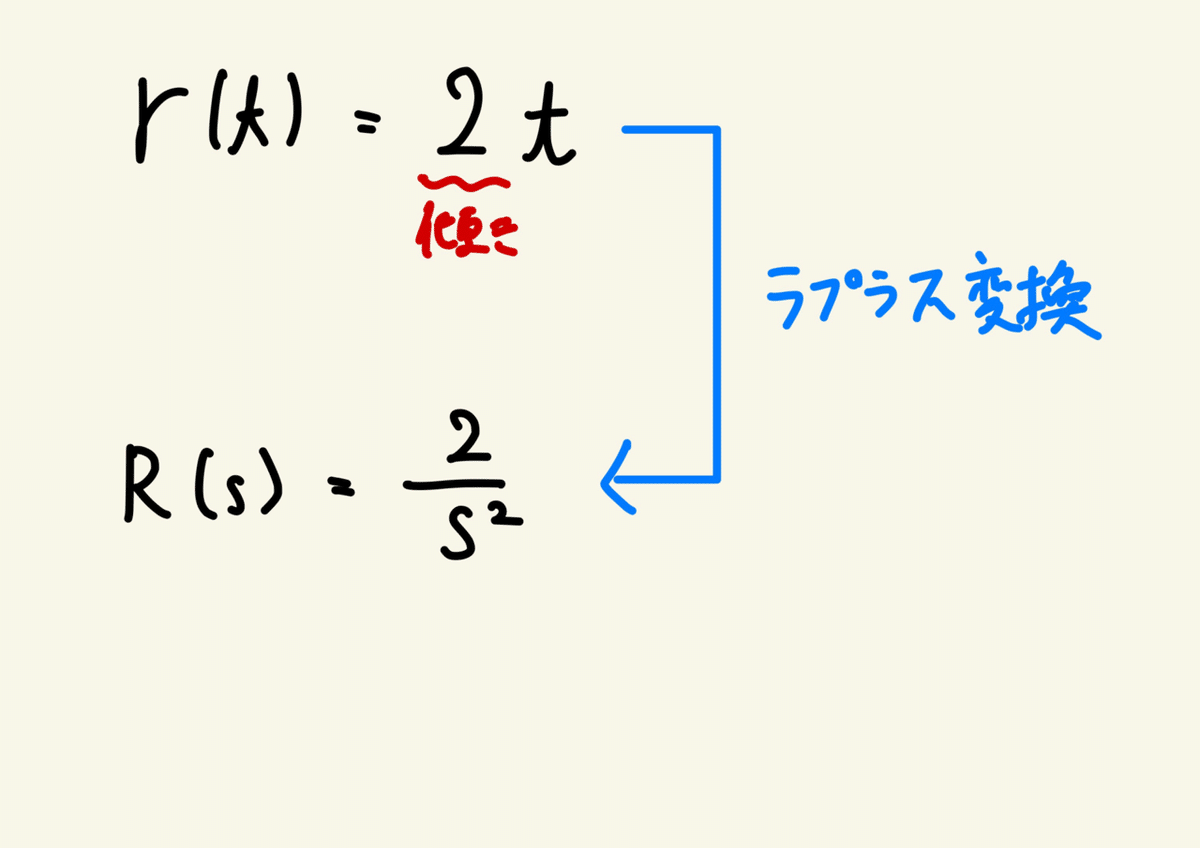
ラプラス変換はまた別でまとめると思うので今回は省きます。
K=2をEの式に代入する、ついでに因数分解も。

これで準備完了。
定常偏差はラプラスの最終値の定理を使用して求める、その式は

計算していくと

答えは0.4となる。
⑸について。
使用していた問題集に似たような問題があったが理解できなかったやつ。
公式解答を参考にするとまずはEの式を書く。
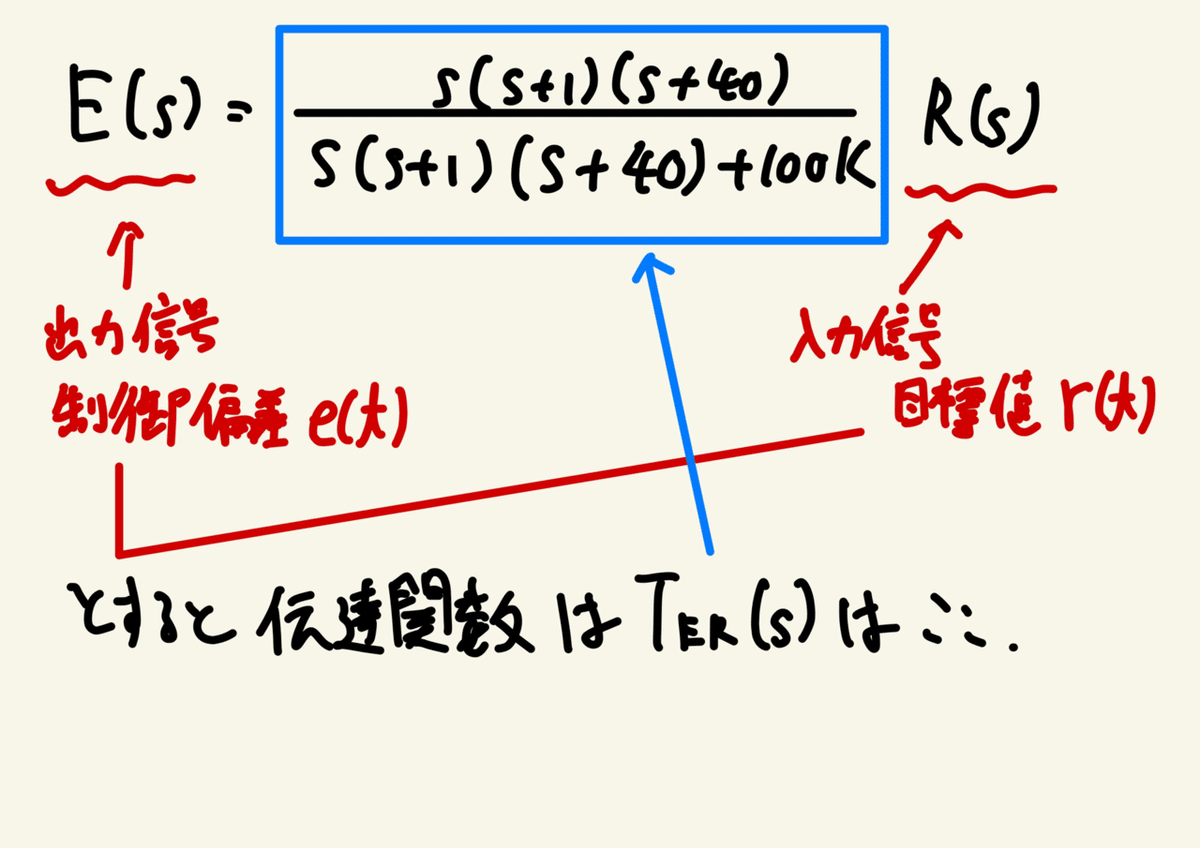
これはまあここまででも求めてたやつね。

問題文で入力も出力も正弦波とあるので周波数伝達関数の絶対値倍ということかな。
で、とりあえずω=1を入れて考えると。

伝達関数の絶対値は0.34564であることがわかり、入力、出力、伝達関数を見比べてみると

振幅が2だから0.34564をかけて
答えはB=0.691になる。
うーん、わかったようなわかっていないような…
間違いなく試験時よりはわかったと思うが、ここも繰り返し必須ですね。
そんなわけで予想得点は⑷まで完答と仮定して24点。
機械制御は合計で45点と予想している。
あとがき
これで終わり。
冷静に考察してみて良くて99点といったところかな。
あと9点。
電力管理だねぇ…
この辺はミスを防げるように修練を積むしかないでしょう。
まあ、かなり甘く見積もってるので実際はもっと低いかもしれませんが…
一回目よりは勉強した分だけ点数増えたし、やり込むしかない。
ということで2022年度の復習はこれでようやくおしまい。
ちょっとだけ予定よりオーバーしましたがちょうどエネルギー管理士の日程も発表されましたし、電験二種一次に向けて切り替えていく。
ではでは〜