
新型コロナウイルス、体内に侵入したウイルス数が多いと、より危ない説
新型コロナウイルスの記事です。
ずっと気になっていたんですが、人体の免疫細胞の数には限りがあるので、どんなにワクチンで免疫防衛力を上げても、免疫細胞の防衛力を遥かに上回る数のウイルスを体内に侵入させたら死ぬのではないか?という疑問を常々持っていたんです。
言い換えると、「感染時のウイルス侵入数には、絶対に勝てない限界値があるのではないか」ということです。人体実験するわけにはいかないので、これをモデル化して理論的に検証してみました。
なお、本記事は、数学的には算数レベルの計算しか出てきませんので、値を当てはめればだれでも計算できます。生物学的にはちょっと高度で、高校生物の免疫を修得しているか、あるいは漫画「はたらく細胞」
を読破している必要があります。
モデル化
人体におけるウイルスとの戦いは、ウイルス攻撃力(増加するウイルスの数)VS 人体防衛力(B細胞をはじめとするウイルス破壊システム)の綱引きとしてモデル化できるとします。

モデルにおける事実と推測
モデルを構築するには、「ほぼ間違いない前提となる事実」を元に、「妥当な推論」を仮説として立てて、それに合った数式を考えます。

実際の計算
計算には、いくつかの値を仮定する必要があります。
体内に侵入したウイルス数をαと表記し、10と仮定します。
ウイルスの増殖力をvと表記し、100と仮定します。つまり、6時間で100倍になります。ちなみに、実際にはv=1000以上と考えられていますが、とりあえず試算なので見やすい数にしました。
人体の防衛力をB=9990000000とします。びっくりするぐらい多い値ですが、これぐらいないと抑えられないのです。あとで解説します。とりあえずは計算の様子だけご覧ください。

免疫応答は、ウイルスが侵入して即行われるわけではありません。大体1日以内のタイムラグがあります。そこで、時間tを6時間ずつ進めるとして、t=1で感染後6時間、t=4で24時間となります。免疫はt=4の24時間目に初めて本格稼動するとすると、t=3まではBによる防衛は0となります。したがって、すき放題増えます。また、防衛力Bは、免疫細胞の増殖と共に増大するのですが、本モデルではすでにワクチンによりフル装備となっていることを仮定しています。
ウイルスは10、1000、100000と増大していきますが、4ステップ目で防衛力が一気に発動し、5ステップ目には0となりました。これは発症せずに無事押さえ込めた例です。
考察
では、本方程式を用いて、免疫の勝敗がどのように決まるか、どのあたりに限界があるのかを見ていきます。あくまで理論値ですが、この方程式がどのように振舞うかを観察することで、ウイルスの侵入数が戦いにどう影響するのか推測できます。

実際にグラフ化してみると、ウイルス侵入数は極めてシビアな影響を与えることがわかります。本シミュレートでは、初期値1、増殖倍率2でなんとか終息するようにB=11を固定値とします。この仮想的な人体に、ウイルスが2個、つまり2倍侵入した場合、ウイルス数は防衛力を振り切って発散します。これは人間側の圧倒的負けです。
ではどこが分岐点となるかというと、1.375個。例えるなら、値を100倍してみると、ウイルスが100個侵入しても大丈夫な人間で、137個までは耐えられる可能性があるが、138個だと負ける可能性が高いということになります。
注目すべきは、初期感染数αの細かさ。ほんのちょっとした増加で手がつけられなくなる可能性を示唆しています。
どう勝ったか
勝利した戦いを見てみましょう。
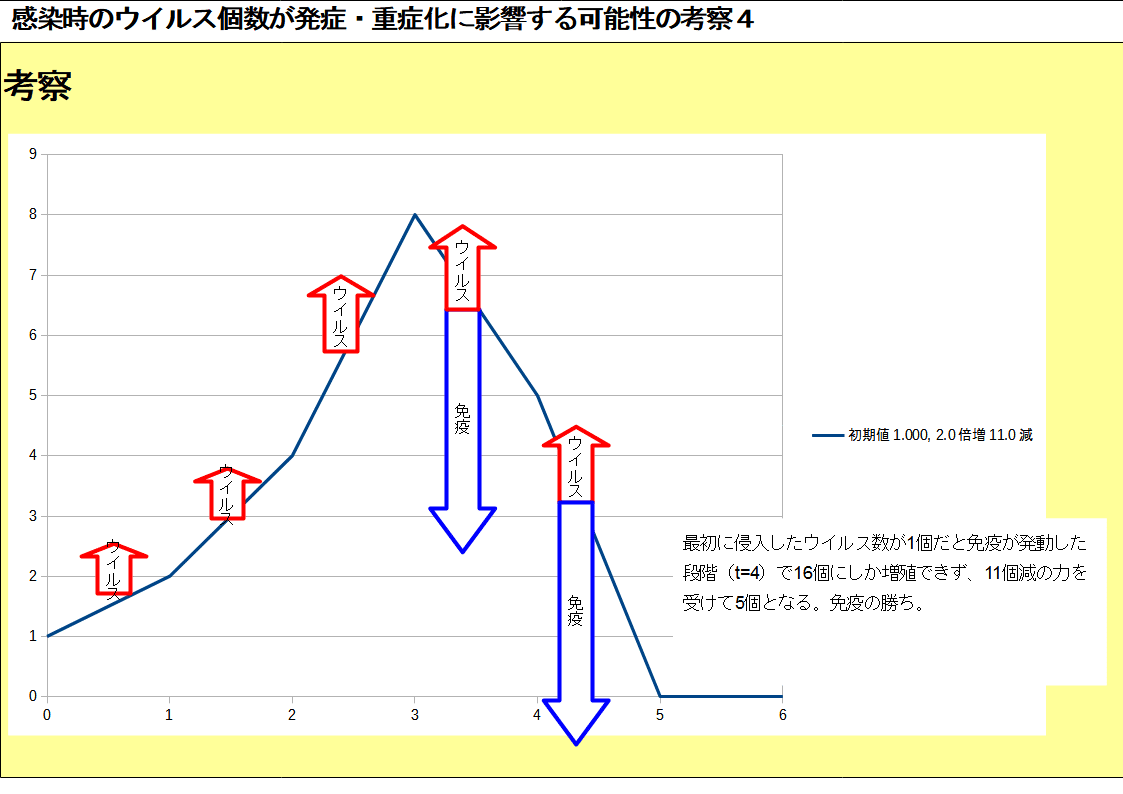
倍、倍に増える中、増加数が免疫の能力を上回らなかったために押さえ込めました。当然といえば当然です。
どう負けたか
敗北した戦いを見てみましょう。

4ステップ目に入るときに11個のウイルスを減らす力がありますが、感染時に既に2倍の兵力を持ち込まれているので、抑えきれません。あとはしばらくジリ貧の戦いの後、一気に押し込まれて負けます。
方程式が意味するもの
この方程式は、実測値に基づいたものではないため、確定的なことはいえません。ただし、方程式の観察により、以下のことがいえそうです。また、現実をある程度反映していると考えると、マスク等でウイルスの絶対数を減らすことの大切さを示すひとつの根拠になりえます。





結論
少なくとも、初期感染数の多さがウイルスに有利に働くならば、マスク等でウイルスの数を減らすことは大切。また、いくら免疫がついていても、マスクもせず、35億個しかないB細胞(しかもコロナ対応できるのはごく一部)に数万、数十万のウイルスをぶつければ激戦は避けられないと思います。
可能であれば、マスクをつけ続けること、感染防止策を可能な限り続けることを提案したいと思います。
おわり。
