【東京工業大学2020年度前期入試数学第5問】トライ＆エラーを繰り返して攻略する極限問題

いよいよ最後の問題です。積分と数列の極限の問題です。東工大ではときときこの手の問題が出題されています。

東京工業大学　本館
2011年5月19日、03撮影、Wikipediaより

[問題] k を正の整数とし，a(k) = ∫_{0}^{1} x^{k-1} sin(πx/2) dx とおく．
(1) a(k+2) を a(k) と k を用いて表せ。
(2) k を限りなく大きくするとき，数列 {ka(k)} の極限値 A を求めよ。
(3) (2) の極限値 A に対し，k を限りなく大きくするとき，数列
　　　　　　　{ k^m a(k) - k^n A }
が 0 ではない値に収束する整数 m, n (m > n ≧ 1) を求めよ。またそのときの極限値 B を求めよ。
(4) (2) と (3) の極限値 A, B に対し，k をk を限りなく大きくするとき，数列
　　　　　　　{ k^p a(k) - k^q A - k^r B}
が 0 ではない値に収束する整数 p, q, r (q > q > r ≧ 1) を求めよ。またそのときの極限値を求めよ。

(注) a(k) の定義が分かりにくいと思いますので、以下に示しておきます。(実際には a(k) は a に 下付き文字の k です。)

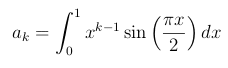
(1) は基本的だと思います。特に問題ないかと思います。

この手の問題は東工大に限らず、いろいろな大学で出されています。

(2) ですが、いくつかの証明方法がありそうですが、まず a(k) → 0 を証明します。

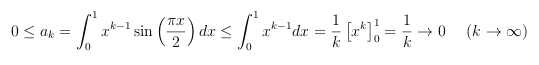
これと (1) の漸化式を利用して、

より、ka(k) → 1　(k→∞) とするのがきれいだと思います。よって、A = 1。

(3) は、(1) を変形して

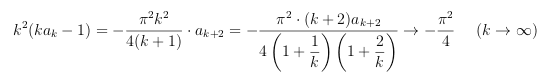
から m = 3, n = 2 のとき B = -π^2/4 と求まります。

ちなみに、これ以外では条件を満たしません。一応確認しておきます。

まず、k^m a(k) - k^n A = k^n (k^{m-n} a(k) - A) となりますが、k → ∞ のとき k^n → ∞ であるので、収束するには k^{m-n} a(k) → A である必要があります。

したがって、m = n + 1 となり、このとき、n ≧ 3 であるならば k^m a(k) - k^n A → ∞ となり、n = 1 のときには k^m a(k) - k^n A → 0 となるので、条件を満たすのは上記のみとなります。

(4) も似たようなものです。さらに丁寧に変形するだけです。

ということで、p = 4, q = 3, r = 1 のときに k^p a(k) - k^q A - k^r B は 3π^2/4 に収束します。

(4) の解がこれ以外にないことも確認する必要がありますが、(3) と同じように考えます。

k^p a(k) - k^q A - k^r B = k^r (k^{p-r} a(k) - k^{q-r} A - B) となり、k → ∞ のとき k^r → ∞ であるので、k^{p-r} a(k) - k^{q-r} A → B である必要がありますが、それを満たすのは (3) より p - r = 3, q - r = 2 となります。

このとき、k^p a(k) - k^q A - k^r B = k^r (k^3 a(k) - k^2 A - B) となりますが、上記の結果から r ≧ 2 のときには∞に発散することになるので、上記以外に収束することはあり得ないことになります。

この問題はいろんな点で難航することが予想されます。

(2) は答えは予想付くと思いますが、処理に困るかもしれません。(3) と (4) はもっと処理に困るのではないかと思います。

(注) ka(k) が定数に収束するならば a(k) は 0 に収束するので、(1) の答えから ka(k) は 1 に収束する以外にあり得ないことになります。ということで、(2) の答えは簡単に予想がつきます。

上記の通り、(3) と (4) において私の場合はピンポイントで収束する場合を見つけて式変形していますが、どうして見つかったかと問われても説明できません。笑

例えば、(4) の場合は k^2(ka(k) - 1) + (π^2/4) を計算して、式を変形して眺めている中で上記の式を見つけています。上記の式変形は最短の手続きで行っていますが、実際に導いたときには回り道してたどり着いています。

この辺りは感覚的なところなので、皆さんが同じ過程をたどるとはとても思えません。私より早くに気が付く方もいらっしゃるだろうし、時間がかかる方もいらっしゃるでしょう。解けない方がいても不思議ではありません。

また、計算もうっとうしかったいるすので、スムーズにいったとしてもそれなりに時間がかかることが予想されます。

ということで、(1) はともかく、それ以降の問題は、時間がかかりそうなら逃げの一手だと思います。他の問題の難易度と比較して最後に回してかまわないと思います。

ただし、相性のいい受験生も少なからずいらっしゃると思いますので、そういう場合は確実にこの問題を取るのがいいと思います。