【京都大学2001年度前期入試数学(理系)第6問】解法の前にまず答えを予想する

今回は京都大学2001年前期入試(理系)の第6問を取り上げたいと思います。どちらかというと東工大っぽい問題です。ということで私の独壇場です。笑

京都大学　百周年時計台記念館
2015年5月5日、Soraie8288撮影、Wikipediaより

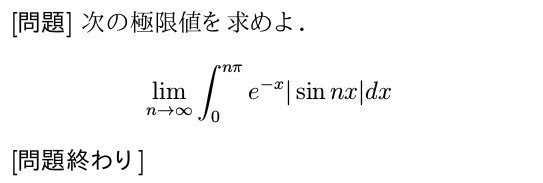
これを見て答えが予想できる人はどのくらいいるでしょうか？

この手の問題は答えが予想できるかどうかで問題を解く速度に差が出ます。それどころか予想できないと解けないことも考えられます。

逆に予想できるならある程度方針が立つはずです。

ということで、答えを予想してみます。

まず、e^{-x}を取り除くとどうなるかを考えてみます。| sin nx | は 0～π/n の範囲を繰り返す周期関数なので、この範囲で積分を求めると

となります。関数の平均値をとると (2/n) ÷ (π/n) = 2/π となります。n が大きいときは関数 | sin nx | の値は頻繁に大小しますが、交流電圧と同じで何となく値 2/π を取る定数関数に見えてきます。(ぼんやりとしたイメージ)

一方、| sin nx | を取り除くと次のように簡単に計算できます。

これに先ほどの 2/π をかけて、何となく答えが 2/π に絞れてきます。

この辺りまで考えると私の中で大体の方針が立ちます。

(書いたものに修正を加えてはいますが、初稿は実は問題を解きながら書いていました。)

(1) π/n ごとの区間に区切る。( [i×(π/n), (i+1)×(π/n)] ごとに積分を考える。)
(2) (1) の区間内で exp(-(i+1)×(π/n)) ≦ e^{-x} ≦ exp(-i×(π/n)) と考える。
(3) (2) の全ての辺に | sin nx | をかけて、(1) の区間で積分する。
(4) (3) の結果の左辺と右辺の極限を取ってはさみうちの定理を使う。

この方針の肝は、sin nx は n が大きいと周期が小さくなる一方、一周期の間に e^{-x} の値は殆ど変わらないので定数関数で近似できるという感覚です。

ここまで解析できれば問題は解けたも同然です。(おそらく入試でも同じ感触でいると思います。)

ここからざっくり解答

さて、方針の通りに考えてみましょう。まずは | sin nx | の値の正負が変化しない区間で分けます。

次に、分けられた各々の区間について exp(-x) を上と下から評価することで、上式を評価します。(積分計算は簡単なので省略しています)

これを最初の式に代入します。

この両辺は次のように同じ値で挟まれることになります。(区分求積法を思い浮かべてください。)

ということで、はさみうちの定理より以下の式が成り立ちます。

答えは予想通り 2/π となりました。

別解

さて、問題の式の極限の中にある定積分ですが、実は求めることも可能です。

が成立するので、

となります。e^{-x} は下に凸の単調減少関数であるので、区分求積法を用いると

と

が成り立ち、先ほどの式に代入すると次の不等式が言えます。

ここで両辺の極限を求めるわけですが、明らかに

が成立するため、はさみうちの定理より

が求められます。

以下、感想

この解答を読むと簡単に見えますが、実際に解こうと思うと難しく感じると思います。結構しんどい。

最初の解法を選択した場合、この問題の鬼門となるのは、はさみうちの定理を利用するための不等式を自力で得るところです。

私はノーヒントであっさり導いてますが、そこには関数に対しての一定の理解が必要になります。

東工大の受験生は誘導問題なしで不等式を確立して証明する問題に慣らされているので、このくらいのことは出来ても不思議ではない。

こういう問題は東工大では頻出なので(だったので)、絶対に対策をしなければならないタイプの問題でした。

しかし、誘導問題なしで不等式を立てることを要求する大学は殆どありません。おそらく、それでは試験にならないからだろうと思います。

東大や京大でも頻繁には出題しないので、京大受験生がこの手の対策を立てている可能性は低いかもしれません。

あくまで傾向と対策の話なので、東工大ではこういう問題で実力を測ってくるし、東大や京大は別のやり方で実力を測ってきているだけです。

京大でこの問題を出すのは通常ではないので、困った受験生は多かったかもしれません。裏をかいて落としにかかったと思って間違いないと思います。

後者の解法の場合ですが、e^{-x} sin nx の不定積分を求める方法は割と知られている(と私は思っている)ので、京大の受験生ならばこちらを選択した可能性は高いと思います。

この方法でも最後にさみうちの定理が待っていますが、こちらは区分求積法の証明そのもの(方法が同一)ですので、割とすんなり行けたかもしれません。

とはいえ、こなれていないと難しい処理が多いので、正答率はそれほど高くないと思います。私の感覚では、この問題の出来は合否を分けた可能性があると思います。そのくらい、ちょうどいい難易度だと思います。

仮にそうでなかったとしても、一定数の受験生を振るい落とす、もしくは逆に、上位層を決定づけるには十分だったのではないかと思います。

この手の積分＆極限の問題は忘れたころに難関大学でお目にかかるので、京都大学の受験生に限らず、こういう問題をスマートに解く術を磨いておきたいところです。