
機械学習を用いてGTO戦略を理解するPart IV 〜Shapley Additive Explanation(SHAP)を用いたGTO戦略のミクロ・マクロな理解〜
今回のnoteの最後には投げ銭部分を用意していますが、全文無料で見ることができます。
今回のnoteで取り組んだこと&結論
Part IIIでは各特徴量のマクロな振る舞いを表現するpartial dependence (PD)という指標を紹介しました。
今回のnoteでは、個別のボードに対して、その予測の理由づけを行うShapley additive explanation (SHAP)を紹介し、そのSHAPがミクロな解析にも、マクロな解析にも両方使えることを示します。
今回のnoteで取り組んだことおよび結論は次です:
SHAPによる各ボードにおける各特徴量の解析(ミクロ)
特に(1)K22r, (2)QsJs9hという2つのボードでの25%CB頻度を解析しました。
その結果、K22rのボードではIPの強いレンジが部分が濃く、弱いレンジが薄いことが、bet頻度を高める要因になっていることがわかりました。
QsJs9hではQ、J、9といったカードが4bet callerのレンジに非常にマッチしているため、相対的にIPの強いレンジが非常に少なくなり、代わりに中EQをもつハンドが増えていることが、25%CBの頻度を低下させることがわかりました。
SHAPによる全ボードでの各特徴量の解析(マクロ)
全ボードでの結果を図解し、(1)どのような特徴量が重要か、(2)どのような特徴量によって25%CB頻度が増減するのか、全Flopでの傾向を解析しました。
重要度では、PFIと似たような傾向を示すことを確認しました。
25%CB頻度の増減についても、PDと似た傾向を示すことを確認しました。
概要
Part IIIでは、学習したモデルにpartial dependence (PD)を適用し、各特徴量のマクロな振る舞いを解析しました。しかし、さまざまなボードでの平均的な振る舞いだけではなく、個別ボードの性質を解析したいことがあります。
ポーカーは非常に複雑なゲームであり、CB頻度には、ボードに対するレンジの強さ、ポジション、ドローの多さなど多くの要素が関わっています。
この下で、1つボードを固定したとき、各要素がどの程度予測値に影響しているのかを知り、個別ボードの理解度を高めたい気持ちになることがあります。
SHAPはこのような要望に応えるよう設計された手法であり、予測値の各特徴量への寄与度を足し算の形で分解します。
例えば簡単のため、あるボードにおける25%CB頻度 $${\phi}$$ がハイカード・IP EQB・OOP EQBの三つから説明できるとします。この時、SHAPを用いると、 $${\phi}$$ が以下のような形に分解できます:
$$
{\phi = \phi _{avg} +\phi_{high} + \phi_{IP}+\phi_{OOP}},
$$
ここで
$${\phi_{avg}}$$ は平均の25%CB頻度
$${\phi_{high}}$$ はハイカードの予測に対する寄与度
$${\phi_{IP}}$$ はIPのEQBの予測に対する寄与度
$${\phi_{OOP}}$$ はOOPのEQBの予測に対する寄与度
です。
つまり、SHAPは平均からの予測値の乖離度を、各特徴量の足し算の形で分解することを可能とします。また、特徴量が増えた場合も同様です。
以下にK22rのボードにおける、25%CB頻度をSHAPを用いて解析した結果を示します。

のちに詳しい見方を説明しますが、個別の要因の予測値に対する影響度を可視化できています(ミクロな解析)。
また、様々なボードにおける各要素の影響度をプロットすることで、PDのように各要素の平均的な振る舞い(マクロな解析)も観察することが可能です。これものちに詳しく紹介します。
SHAP自体のコンセプトは、本記事の付録に記載したので興味がある方は見てみてください。
実験
準備
Part I・IIと同様に以下の状況を考察しました。
100bb BB vs LJ (4bettor)の4bet pot(注1)の25%CBの頻度の予測を対象とします。
pot sizeは50.5bb、残りスタックは75bb
betting sizeの設定は次のようにしました。

次に、PioSOLVERを用いて、被りのない1755flop全てでのゲームツリーを生成し、OOP checkのシチュエーションに関してIPのアクションに関する集合分析ファイルを生成しXGBoostというモデルを学習しました。
詳細はPart Iをご参照ください。
SHAP(ミクロな解析)
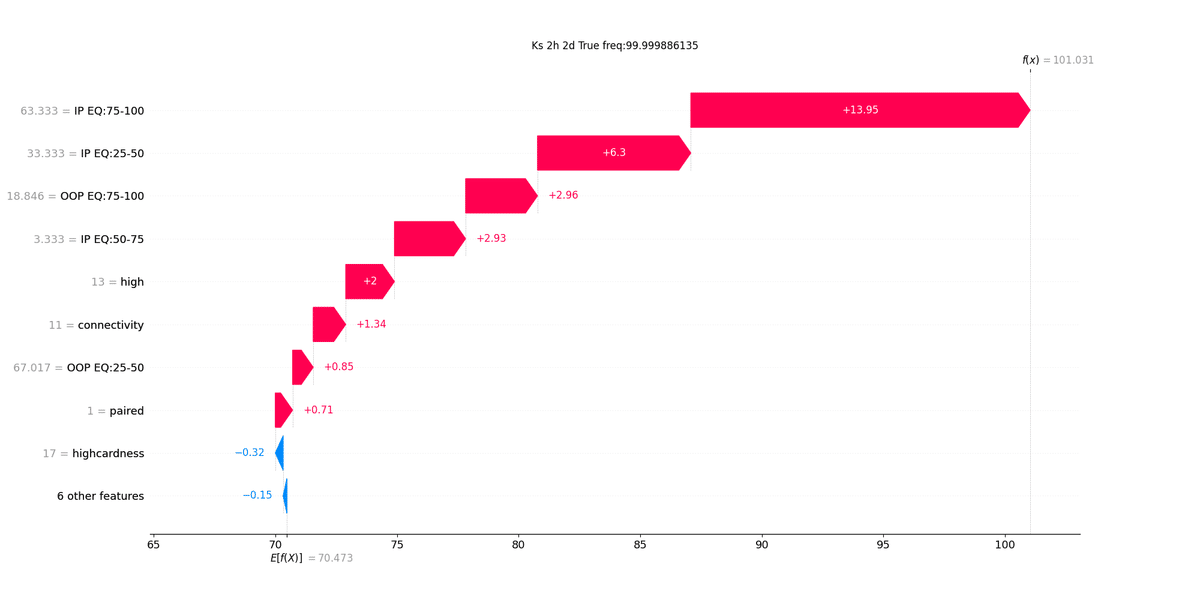
以下にK22rのボードにおける、25%CB頻度をSHAPを用いて解析した結果を示します。

右上の $${f(x)}$$ がモデルの予測値を表しています。このボードにおける真のbet頻度はほとんど100%であり、モデルもそれに非常に近い値を示しています(注2)。
次に、 $${E[f(x)]}$$ が平均値になっています。この図を下から上に見ていくと、平均値に対して、各特徴量がそれぞれどのように足し合わされて予測値に辿り着くのかを見ることができます(水色がマイナス、赤色がプラス)。
このボードにおける出力の解釈は非常に素直です。まず、 IPの強いレンジが部分が濃く、弱いレンジが薄いことが、bet頻度を高める要因になっています。また、OOPの強いレンジが薄いこともbet頻度を高める要因になっています。
他には、Kハイであること、connectしていないことなどがbet頻度の上昇にやや寄与しています。
次に、QsJs9hのボードでのCB頻度を解析します。

このボードは非常に25%CB頻度が少なくなるボードの代表格であり、33%ほどの25%CB頻度を持ちます。
まずQ、J、9といったカードが4bet callerのレンジに非常にマッチしているため、相対的にIPの75-100%のEQをもつ強いレンジが非常に少なくなり(5%程度)、代わりに50-75%ほどのEQをもつハンドが増えています(61.6%程度)。
この2つの要因により、25%CB頻度が大きく下がっています。
この他、connectivityの高さや、lowカードが大きいことなどが25%CB頻度の低下に寄与しています。
SHAP(マクロな解析)
SHAPでは、元々は個別ボードの解析に用いるものですが、複数ボードでの各特徴量の平均的な振る舞いの観察にも用いることが可能です。
まず、PFIのように、SHAPから各特徴量の重要度を定義します。
具体的には、寄与度 $${\phi_i}$$ の絶対値 $${|\phi_i|}$$ の平均値を重要度と考えることができます。
SHAPから計算された重要度を棒グラフにしたのが以下です:

この重要度は、PFIと概ね整合的です(注3)。

また、様々なボードにおける、各特徴量がある値を取る時の寄与度 $${\phi_i}$$ をプロットすることで、PDのように大まかな傾向を掴むことが可能です。
以下の図は、縦軸が各特徴量、横軸が寄与度であり、各プロットの色がその特徴量の値を示しています(これをbeeswarm plotと呼びます)。また、上から重要度の高い特徴量が配置されています。

この図において、例えばIP EQ 75-100%のところでは、赤い点が右に、青い点が左に寄っていますが、これは75-100%の濃度が高いほど25%CB頻度が高く、濃度が低いほどCB頻度が低くなることを表します。
同様にして、この図から得られる知見は以下です:
IPの強いレンジ(IP EQが75-100%)が増えるとCB頻度が上がる。
IPの弱いレンジ(IP EQが25-50%)が増えるとCB頻度が下がる。
IPの中程度の強さのレンジ(IP EQBが50-75%)が増えるとCB頻度が下がる。
highカードが大きくなるとCB頻度は上がる。
OOPの弱いレンジ(OOPP EQが25-50%)が増えるとCB頻度は上がる。
connectしているボードではCB頻度が下がる。
monotoneボードではCB頻度が下がる。
OOPの強いレンジ(OOP EQが75-100%)が増えるとCB頻度が下がる。
これらの知見はPDで得られた知見と概ね整合的です。
まとめ
今回のnoteでは以下のことに取り組みました。
SHAPによる各ボードにおける各特徴量の解析(ミクロ)
特に(1)K22r, (2)QsJs9hという2つのボードでの25%CB頻度を解析しました。
その結果、K22rのボードではIPの強いレンジが部分が濃く、弱いレンジが薄いことが、bet頻度を高める要因になっていることがわかりました。
QsJs9hではQ、J、9といったカードが4bet callerのレンジに非常にマッチしているため、相対的にIPの75-100%のEQをもつ強いレンジが非常に少なくなり、代わりに50-75%ほどのEQをもつハンドが増えていることが、25%CBの頻度を低下させることがわかりました。
SHAPによる全ボードでの各特徴量の解析(マクロ)
全ボードでの結果を図解し、(1)どのような特徴量が重要か、(2)どのような特徴量によって25%CB頻度が増減するのか、全Flopでの傾向を解析しました。
重要度では、PFIと似たような傾向を示すことを確認しました。
25%CB頻度の増減についても、PDと似た傾向を示すことを確認しました。
これらを通して、SHAPがミクロにもマクロにも戦略を解析できる手法であることを示しました。
結論
全4回のnoteを通して、以下のことを紹介しました。
Part I: 機械学習の概要およびXGBoostを用いたアクション推定モデルの構築
Part II: Permutation Feature Importance (PFI)を用いた、アクション頻度を決めるにおいて重要な要素の抽出
Part III: Partial Dependence (PD)を用いた、入出力のマクロな関係の理解
Part IV: Shapley Additive Explanation (SHAP)を用いたミクロ・マクロ両側面の戦術の理解
予測モデルの構築から始まり、構築したモデルのミクロ・マクロの解析方法を紹介しました。
機械学習を用いたGTO戦略の解析手法の一つの方法論を提示しました。
また、今回はレンジ全体の特に25%CBのみに注目しましたが、今後はその他の戦略や、レンジ全体の戦略をgivenにした下での、ハンドレベルでの戦略の解析を行おうと考えています。
質問・コメントなどは@Yuck_PCPまでお願いします。
フォローやスキ(いいね)してくれると大変嬉しいです。
このnoteはhyugaさんおよびたこあげまつりさんの協力で制作されました。
(付録)SHAPのコンセプト
SHAPは協力ゲーム理論から派生した概念です。協力ゲーム理論ではプレイヤー間の協力によってもたらされた利得をどのように分配すべきかが分析の中心となります。
まず協力ゲーム理論のゲームの一例としてアルバイトゲームを説明し、そのゲームでの利得分配方法としてShapley値を説明します。その後Shapley値を用いたXAI技術の一つであるSHAP(SHapley Additive exPlanation)の説明をします。
アルバイトゲームとは複数人が与えられた時、その中のいくつかの人(これは1人でも全員でも構いません)が協力してアルバイトをし、その報酬が与えられるゲームです。岡田(2011)にならい、参加者がA・B・Cさんの3人であるとして、次の表で報酬が与えられるケースを考えます。
$$
\begin{array}{|c|c|} \hline
参加者 & 報酬 \\ \hline
Aさんのみ & 6 \\ \hline
Bさんのみ & 4 \\ \hline
Cさんのみ & 2 \\ \hline
A・Bさん & 20 \\ \hline
A・Cさん & 15 \\ \hline
B・Cさん & 10 \\ \hline
A・B・Cさん & 24 \\ \hline
\end{array}
$$
この下で、A・B・Cさんが参加した時の報酬24はどう3人で山分けるのが公平でしょうか。
これを考えるために、A・B・Cさんをあらゆる順番(A→B→C、A→C→B、B→A→C、B→C→A、C→A→B、C→B→Aの6通り)で追加した時の報酬の増加分を考えます。
まずAさんに注目します。するとAさんの追加の仕方は次の組み合わせに限られます。
誰もいない→Aさんのみ(A→B→C、A→C→B) 6-0 = 6
Bさんのみ→A・Bさん(B→A→C) 20-4 = 16
Cさんのみ→A・Cさん(C→A→B) 15-2 = 13
B・Cさん→A・B・Cさん(B→C→A、C→B→A) 24-10 = 14
故に、Aさんを追加することによる報酬の増加分の平均は(6×2+16+13+14×2)/6=11.5であり、これがA・B・Cさん3人で協力してアルバイトするときのAさんの貢献度と考えることができます。
また、同様にするとBさんは8、Cさんは4.5の貢献度を持ちます。また、3人の貢献度は足すと24になり、3人で働いた時の報酬に一致します(注4)。
故に、A: 11.5、B: 8、C:4.5と山分けするのが、「公平」な分配の一つと考えられるわけです。
こうして得られた貢献度をShapley値と呼びます。同様にして多人数の場合も定義することができます。
次にこれを機械学習に応用することを考えます。いまA・B・Cの3つの特徴量があり、その3つの特徴量を入力として、1つ出力を出すモデルを考えます。この下で、各特徴量の予測値に対する寄与度を出したいのですが
アルバイトゲームのプレーヤー→特徴量、具体的にはAさんが参加する=特徴量Aがわかっている。
報酬→特徴量
と類推することで、各特徴量の予測に対する寄与度を求めることが可能です。
1つ注意点としては、「特徴量Xがわかっている」というのをどう表現するかです。
これは単にわかっている特徴量以外の特徴量で期待値を取ることで解決できます。例えば特徴量Aが $${A=a}$$ とわかっているとき、学習した機械学習モデル $${f}$$ について
$$
{E_{B,C}[f(a, B, C)],}
$$
つまりB・Cについて期待値をとったものを、特徴量Aがわかっているときのモデルの出力と考えることができます。
そしてこの期待値操作を、与えられた検証用のデータでの $${(a_1, a_1, c_1), \dots, (a_n, b_n, c_n)}$$ について
$$
{\frac{1}{N}\sum_{i=1}^n f(a, b_i, c_i),}
$$
として近似することで、具体的な出力を評価することができます。
これをさまざまな特徴量の組み合わせにおいて評価することで、各特徴量の予測に対する寄与度を求めることが可能になり、これをSHAPと呼びます。
以上の議論を数学的に精緻に議論するとかなり煩雑になるので細かな定義はここでは取り上げませんが、気になる方は以下のページなどをご参照ください。
レンジは3 million poker club (3MPC)配布のこちらのレンジを使用。↩︎
モデルの出力を特に0-100%の間に制限していないので、時々この範囲をはみ出す出力をだすことがあります。↩︎
特徴量の順序が一部異なっていますが、これはPFIが誤差を用いて重要度を定義してるのに対して、SHAPは予測への寄与度を重要度の定義に用いており、シンプルに定義が異なるため順序も異なっています。↩︎
これが一致する理由は実際に式を計算してみるとわかります。↩︎
ここから先は
¥ 300
Amazonギフトカード5,000円分が当たる
この記事が気に入ったらチップで応援してみませんか?
