
機械学習を用いてGTO戦略を理解する Part III 〜Partial Dependence (PD)を用いたGTO戦略のマクロな理解〜
今回のnoteで取り組んだこと&結論
Part IIではボード・ハンドの情報からアクションの頻度を予測するモデルにおいて、重要度の高い特徴量をpermutation feature importance (PFI)を用いて特定する方法を紹介しました。
Part IIIでは、それぞれの特徴量を変化させた時に、アクション頻度がどう変化するかをpartial dependence (PD)を用いて解析していきます。今回のnoteで得られた解析結果は次です。
IPの強いレンジの割合が多くなるほど25%CBの頻度が上がる。同時にIPの中程度〜弱いレンジの割合が多くなるほど25%CBの頻度は下がる。
OOPの強いレンジが増えると25%CB頻度はやや下がる。OOPの弱レンジが増えると25%CB頻度はやや上がる。中程度の強さのレンジは25%CB頻度にそこまで影響を与えない。
ボードのハイカードが大きくなるにつれ25%CBの頻度はやや上がる。Kハイボードが最も頻度が大きくなる。
monotone boardでは25%CBの頻度はやや下がる。
ボードがコネクトしなくなるほど25%CBの頻度はやや上がる。

概要
Part IIでは予測モデルの入力の重要度をPFIで定量化したところ、
IPのEQBが特に重要。
OOPのEQBはやや重要。
high、monotone、connectivityはやや重要。
ペアボードであることやsuitedであることはあまり重要でない。
ということがわかりました。

この下で、もう少し細かい情報が知りたくなります。具体的には、入力を変えた時に、アクションの頻度がどう変わるのか(e.g. IPが強いレンジを多く持つとき、25%CB頻度はどう変化するのか?)といったことを知りたくなります。
PDはこのようなことを解析したい場合に有効な指標です。具体的には、ある特定の特徴量が変化する際の、モデルの出力への平均的な影響度を視覚的に表現するための指標です。
具体的には次のようなグラフが手に入ります。

こちらはIPのEQBの75%-100%(強いレンジ)の割合を増やした時のCB頻度の推移です。強いレンジが増えるほど安いCBの頻度が上がることがわかります。
この指標を用いる利点は、ブラックボックスとなっているモデルをよりわかりやすくしたり、特定の特徴量がどのように予測に影響を与えているか直感的に理解できることです。
なおPDの定義はややテクニカルなので、興味がある方は最後の付録をご参照ください。
実験
準備
Part I・IIと同様に以下の状況を考察しました。
100bb BB vs LJ (4bettor)の4bet pot(注1)の25%CBの頻度の予測を対象とします。
pot sizeは50.5bb、残りスタックは75bb
betting sizeの設定は次のようにしました。

次に、PioSOLVERを用いて、被りのない1755flop全てでのゲームツリーを生成し、OOP checkのシチュエーションに関してIPのアクションに関する集合分析ファイルを生成しXGBoostというモデルを学習しました。
詳細はPart Iをご参照ください。
各特徴量のPD
得られたPDのうち、PFIで重要と判断されたものをピックアップして記載します。
以下のグラフでは縦軸は平均的な25%CB頻度と考えていただいて結構です。
IPのEQB



EQBとはequity bucketのことを指し、IPのハンド群の相手のレンジに対するエクイティを25%刻みでヒストグラムをとったものを指します。英語ですがこちらの動画などがわかりやすいです。
これらの表は次のことを示唆します。
IPの強いレンジの割合が多くなるほど25%CBの頻度が上がる。同時にIPの中程度〜弱いレンジの割合が多くなるほど25%CBの頻度は下がる。
OOPのEQB


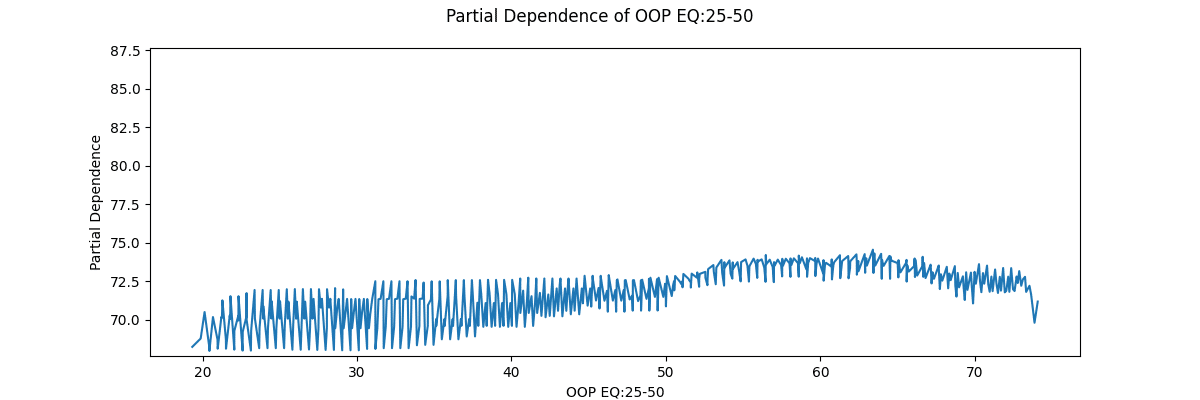
これらの表は次のことを示唆します。
OOPの強いレンジが増えると25%CB頻度はやや下がる。OOPの弱レンジが増えると25%CB頻度はやや上がる。中程度の強さのレンジは25%CB頻度にそこまで影響を与えない。
high, monotone, connectivity



highとはboardの一番高い数字のことを指します。Aは14とします。
monotoneは、1の場合モノトーンボード、0の場合そうでないことを示します。
connectivityはboardの一番高い数字から一番低い数字を引いた値を指します。
これらの表は次のことを示唆します。
ボードのハイカードが大きくなるにつれ25%CBの頻度はやや上がる。Kハイボードが最も頻度が大きくなる。
monotone boardでは25%CBの頻度はやや下がる。
ボードがコネクトしなくなるほど25%CBの頻度はやや上がる。
また、重要ではないと判断されたペアボードやsuitedの振る舞いも確認しておきましょう。
pairedおよびmonotone


pairedは、1の場合ペアボード、0の場合そうでないことを示します。
suitedは、1が2枚使いのflush drawが存在しうるボードで、0がそうでない場合を指します。
それぞれのグラフの縦軸のスケールは、前に提示した5つのものと揃えてあることに注意してください。重要と判断された特徴量群に比べると、これらの特徴量の予測に与える影響はほとんど無視できるレベルのものということがわかります(注2)。
まとめ
今回のnoteでは、特徴量の重要度だけではなく、各特徴量の値を変化させた時のアクション頻度の変化を考察しました。
IPのEQBが特に重要。
OOPのEQBはやや重要。
high、monotone、connectivityはやや重要。
ペアボードであることやsuitedであることはあまり重要でない。
ということがPFIから示唆されていたわけですが、これらのより深い検証をPDを用いて行うことができ、25%CB頻度に対する理解度をより高めることができました。
次回Part IV(最終回)では、Shapley additive explanation (SHAP)を用いて、個別ボードの解析およびマクロな解析の両面を行なっていきます。
質問・コメントなどは@Yuck_PCPまでお願いします。
フォローやスキ(いいね)してくれると大変嬉しいです。
このnoteはhyugaさんおよびたこあげまつりさんの協力で制作されました。
(付録)PDの定義
このセクションは、ややテクニカルなのであまり興味がない人は読み飛ばしてもOKです。
簡単のため、 X0, X1 の二つの特徴量のみの状況を考えます。学習済みモデル f̂(⋅, ⋅) を持っているとします。この時、 X0 をいろいろ動かすと、モデルの出力がどのように変化するかを知りたいとします。
データ (xi, 0, xi, 1) を考えます。このデータを使って、 X1 = xi, 1 と固定し、 X0 = x0 をいろいろ動かして ŷ = f̂(x0, xi, 1) の値を観察することで、 X1 = xi, 1 に固定した下での出力の振る舞いをプロットすることができそうです。
もちろんこのまま用いても良いですが(注3)、より一般には X1 = xi, 1 に固定せず、いろいろな X1 での出力の平均を観察することで、モデルのさまざまなシチュエーションにおける平均的なプロットを確認することができます。
例えばPart IIで上げた住宅価格の例を考えます。直感的には「部屋数」は住宅価格に大きな影響を与えそうです。
この時、
横軸: 部屋数
縦軸: 部屋数に対応する平均的な住宅予想価格
とプロットすることを考えるとすると、例えば次のようなシチュエーションが考えられそうです。
プロットが右肩上がりであれば、部屋数が増えるにつれて住宅価格も上昇する傾向があることを示します。
プロットが水平であれば、その部屋数の範囲内では部屋数が住宅価格に大きな影響を与えていないことを示します。
このようにして、PDは入力に対する出力の変化を浮き彫りにすると考えられます。
フォーマルには、 X0 = x0 におけるPDは次のように定義することができます:

ここで EX1[⋅] は確率密度関数 p(X1) についての期待値です。しかしこの解析的な量は実際には計算できません。そこで、期待値を与えられた検証用のデータによるサンプリングで代用します:

これをさまざまな X0 = x0 でプロットすることで、ある特徴量を変化させたときのモデルの平均的な振る舞いを知ることができます。また、3変数以上の場合も同様にして拡張することが可能です。
レンジは3 million poker club (3MPC)配布のこちらのレンジを使用。↩︎
25%CBの頻度を予測する上では重要ではないものの、他の75%CBやall-inの予測に対して重要である可能性は否定されないことに注意してください。↩︎
ちなみに、平均を取らないものをindividual conditional expectation (ICE)と呼んだりします。↩︎
