解けるぞと思ったら落とし穴が待っていた数学の問題

こんなの読まないだろうと思った数学のネタを意外に読んでくださる人もいて、しかも間違いを指摘してくださる人まで現れたのには驚きました。

なんで、今日もノリで数学の話を書きたいと思います。

2次方程式って覚えていますか。

はい、これです。これをテキストで表現すると

ax^2 + bx + c = 0

となります。（テキストではｘの２乗というところを「^」の記号で表現します。）

さて問題です。

【問題】２次方程式
ax^2 + bx + c = 0
の解を求めよ。

これを見て、多くの人は、

「あぁー、そんなの中学校でやったな。会の公式ってあったな。もう忘れたけど」

という感じではないでしょうか。

解の公式というのがあって、この方程式を解くと、以下になります。

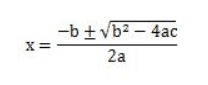
あぁー、なんかそんなのだったな、という人も少なくないんじゃないかなと思います。

これをあえてテキストで表現すると、

x = (-b±(b^2 - 4ac)^0.5)/2a  　　（①）

み、見にくい(笑)

この解の公式は、ax^2 + bx + c = 0 を解いていく（変形していく）ことで導き出せるのですが、今回そこは割愛しますね。

さて、数学を結構頑張っていた人は、公式の導き出し方もちゃんと頭にいれているので紙と鉛筆でちょっと考えたら出せちゃうと思います。

これで答え出た、はいおしまい！、という人。

問題への回答としては、60点です。

えっ、ちゃんと解いたじゃん！と思われますよね。

さらに数学をがっつりやった人達は、これでは回答としては足りないなということに気づきます。（もしくは知っています。）

なにが問題なのか？

この問題、a、b、cの変数になにも条件がついていませんよね。っていうことは、a、b、c がすべての数の場合を答える必要があるんです。

実は、式①では成り立たないパターンがあるのです。

それはなにか。

それは、「aが0のとき」なんですね。

分母にaがあるので、aが0の場合この式は成り立たないのです。

じゃあa＝０のときはどうなるのか。a = 0 を問題の2次方程式にあてはめると、

bx + c = 0　

となります。これを解くと、

x = -(c/b)　　（②）

ということになります。

よし、場合分けもきちんとできた！俺スゲーとここで終わったあなた。

はい、80点です(笑)

これではまだ不十分なのです。それは何か。

それは、「a = 0 かつ b = 0 」のときです。これらを2次方程式にあてはめると、

C = 0

というxにとっては意味のない式になってしまいます。

これはxにとっては解なしと言う事になります。

ここまで回答して、初めて100点です！

まとめますと、

【回答】
a = 0 かつ b = 0 のとき　解なし
a = 0 かつ b ≠ 0 のとき　x = -(c/b)
a ≠ 0 のとき　x = (-b±(b^2 - 4ac)^0.5)/2a 
　

ということなのでした。

2次方程式の問題も、変数に条件がない場合にはここまで答えて初めて正解なのですね。

若かりし頃、この問題を自信満々で回答して60点で悔しい思いをしたので今でも覚えているという(笑)

懐かしいなー。

それではまた！

日々感謝 m(_ _)m