memo1

2024年5月22日 22:59

最適レギュレータ

$$
J＝q_1\int_{0}^{\infty} x_{1}^2(t)dt+q_2\int_{0}^{\infty}x_2^2(t)dt+R\int_{0}^{\infty}u^2(t)dt
$$

Jを最小化するKの導出。

早く収束させたい場合はQを u(t)を過大にしたくない場合はRを大きくする。

QとRを決定する。　
リカッチ方程式によりPを導出する。　
R B PによりKを導出する。

% 状態空間モデルの定義
A = [0 1; -2 -3];
B = [0; 1];
C = [1 0];
D = 0;

% 重み行列の設定
Q = [1 0;0 1]; % 状態の重み行列
R = 1;    % 制御入力の重み行列

% リカッチ方程式を解いてPを求める
[P, L, G] = care(A, B, Q, R);

% 最適フィードバックゲインKの計算
K = -R \ (B' * P);

% 結果の表示
disp('リカッチ方程式の解 P:');
disp(P);

disp('最適フィードバックゲイン K:');
disp(K);

リカッチ方程式の解 P:
    1.2361    0.2361
    0.2361    0.2361

最適フィードバックゲイン K:
   -0.2361   -0.2361

$$
u(t) =\bf{Kx(t)}+G\omega(t)
$$

$$
\omega(t):=\int_{0}^{t}e(\tau) d\tau, e(t)=r(t)-y(t)
$$

l=0.204;M=0.390;J=0.0712;c=0.695;g=9.81;

A=[0 1; -M*g*l/J -c/J];B=[0; 1/J];C=[1 0];D=0;
sys = ss(A,B,C,D);

[A b C D] = ssdata(sys);

sysP = tf(sys)

pole(sys)

Vc = ctrb(A,B);
det(Vc)
rank(Vc)

Vo =obsv(A,C);

det(Vo)
rank(Vo)

可制御行列ctrb()、可観測行列obsv()を作りdetかrankで調べる。

極配置法

l=0.204;M=0.390;J=0.0712;c=0.695;g=9.81;

A=[0 1; -M*g*l/J -c/J];B=[0; 1/J];C=[1 0];D=0;

p(1) = -4+4j;
p(2) = -4-4j;

K = -acker(A,B,p);
eig(A + B*K)

sys = ss(A+B*K,[],eye(2),[]);

t = 0:0.001:1.5;

x0 =[1;0];

x = initial(sys,x0,t);

u = K*x';

plot(t,u);

アッカーマンの極配置アルゴリズムによりKが導出される。1入力系。
極については実部が負側に大きくなると安定度（減衰性）が高くなる。
虚部の絶対値|β|が大きくなると振動周期が短くなる。

最適レギュレータ LQR

l=0.204;M=0.390;J=0.0712;c=0.695;g=9.81;
A=[0 1; -M*g*l/J -c/J];B=[0; 1/J];C=[1 0];D=0;

Q = diag([20 0.001]);
R = 1;
K = -lqr(A,B,Q,R)

重み行列 Qと R を設定することで、LQRにより最適なフィードバックゲイン 𝐾 を導出する。

l=0.204;M=0.390;J=0.0712;c=0.695;g=9.81;

A=[0 1; -M*g*l/J -c/J];B=[0; 1/J];

C=[1 0];
rc = 1;
dc = 1;
x0 = [0;0];

Ae = [A zeros(2,1);-C 0];

Be = [B;0];

q1 = 1e-3;
q2 = 1e-3;
q3 = 5e4;
Q = diag([q1 q2 q3]);
R = 1;

Ke = -lqr(Ae,Be,Q,R);

K = Ke(1:2);

G = Ke(3);

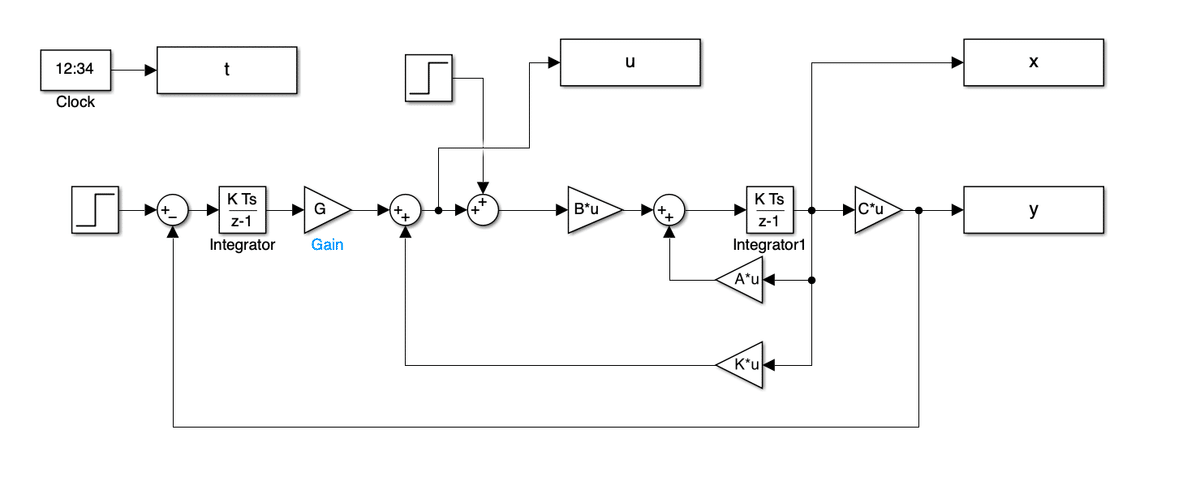
sim('arm_sim_servo')

$$
P:\begin{cases}\dot{x}(t)={\bf Ax}(t)+{\bf Bu}(t),x(0)=x_0
\\\eta(t) = \textbf{x}(t) \end{cases} \tag{2}
$$

(2)に対し有限時間t=tfで任意の初期状態x(0)=x0を任意の状態xfに移す操作量u(t)が存在する。→可制御である。　
可制御ならば必ず可安定。

$$
k:\textbf{u(t)}=\textbf{Kx(t)}, \textbf{K}=\begin{bmatrix}k_{11} & .. \.. & k_{nm} \end{bmatrix} \tag{3}
$$

可制御であることと(3)においてA+BKの固有値を任意の値に設定して極配置を実現可能であることは等価

1入力システムの場合、状態方程式を可制御標準形に変換してKcを設定する方法がある。
可制御標準形に変換する必要がない方法としてアッカーマンの極配置法があり、これは変換する方法と等価である。1入力の場合Kは一意に定まるが他入力の場合Kは無数に存在する。

多入力システムの極配置においてplace関数などがある。これはロバスト極配置法に基づいている。

placeの例　ただしpは入力数を超えて重複してはならない。

A = [1 0 1 2
     1 2 1 0
     0 1 0 2
     1 0 1 1];
B = [0 1
     0.5 0
     0 0
     0 0];

p =[-1 -2 -3 -4];

K = -place(A,B,p)

eig(A + B*K)

Kによりフィードバックされ0に収束する。

clear;
A = [1 0 1 2
     1 2 1 0
     0 1 0 2
     1 0 1 1];
B = [0 1
     0.5 0
     0 0
     0 0];


p =[-1 -2 -3 -4];

K = -place(A,B,p);

eig(A + B*K);

x0 = [0;1;0;0];

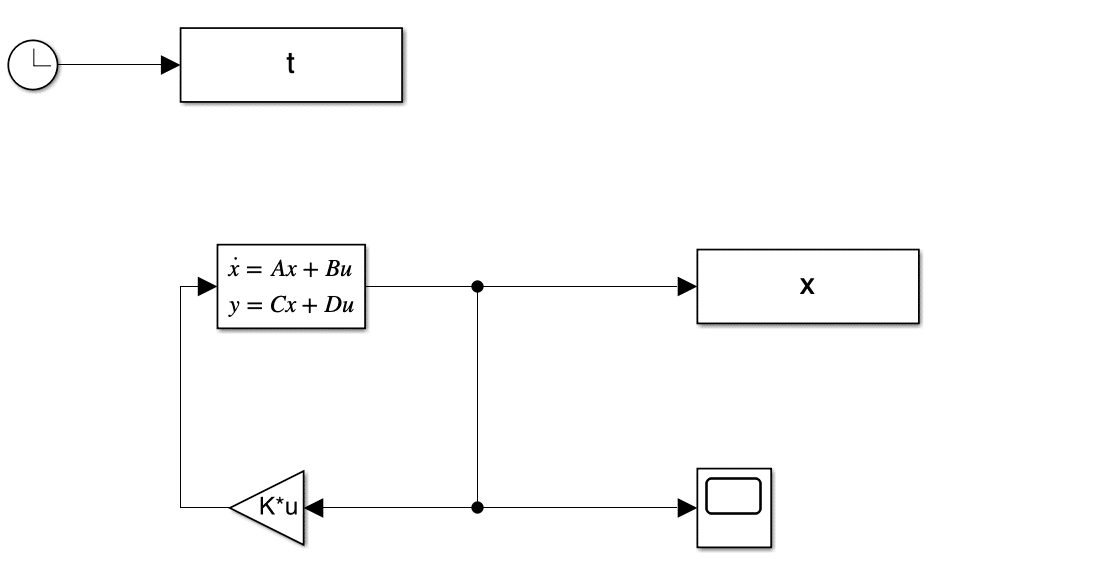
sim('simulink_sfbk');

上記の場合のような目標値が0に収束する場合をレギュレータ制御という。一方特定の目標値に追従させる場合をサーボシステムという。

この場合

$$
k:\textbf{u(t)}=\textbf{Kx}(t)+\textbf{Hy}^{ref}(t) \tag{4}
$$

と目標値に関する項が追加される。これはPDコントローラの拡張とも考えられる。

$$
\mathbf{H} = \begin{bmatrix} -K & I \end{bmatrix} \begin{bmatrix} A & B \\ C & 0 \end{bmatrix}^{-1} \begin{bmatrix} 0 \\ I \end{bmatrix} \tag{5}
$$

(5)のようにKを求めたあとにHを決定し全体のコントローラが決定される。

$$
\textbf{y(s)=P(s)u(s)}, \textbf{P(s)=C(sI-A)}^{-1} \textbf{B+D} \tag{6}
$$

状態空間表現から伝達関数表現への変換に用いるP(s)は伝達関数行列という。伝達関数行列の極とAの固有値は等しい。

$$
| \textbf{M(s)} |=0, \textbf{M(s)} := \begin{bmatrix} -(sI-A) & B \\ C & O \end{bmatrix} \tag{7}
$$

不変零点はM(s)の根sである。s=0の時|M0|≠0の追従制御の条件を満たさなくなる。不変零点は伝達関数行列の各要素の零点と異なる。SISOの場合は伝達関数の零点に等しくなる。

以下のtzeroで不変零点を求めることができる。

% 状態空間モデルの定義
A = [0 1 0 0;
     0 0 1 0;
     0 0 0 1;
    -2 -3 -4 -5];
B = [1 0;
     0 1;
     0 0;
     1 1];
C = [1 0 0 0;
     0 1 0 0];
D = [0 0;
     0 0];

% 状態空間システムの作成
sys = ss(A, B, C, D);

% 不変零点の計算
z = tzero(sys);

% 結果の表示
disp('不変零点:');
disp(z);

ステップ状の目標値、外乱に対し
・システムが内部安定
・コントローラが積分器を少なくとも一つ持つ
・伝達関数が原点s=0に零点を持たない
この条件を全て満たすとき外乱に対する定常偏差が0となることと必要十分条件。

状態フィードバック形式の積分コントローラは以下で表される。

$$
u(t)=\textbf{Kx(t)}+gw(t),w(t):=\int_{0}^{t}e(t)dt \tag{8}
$$

積分なしの追従制御

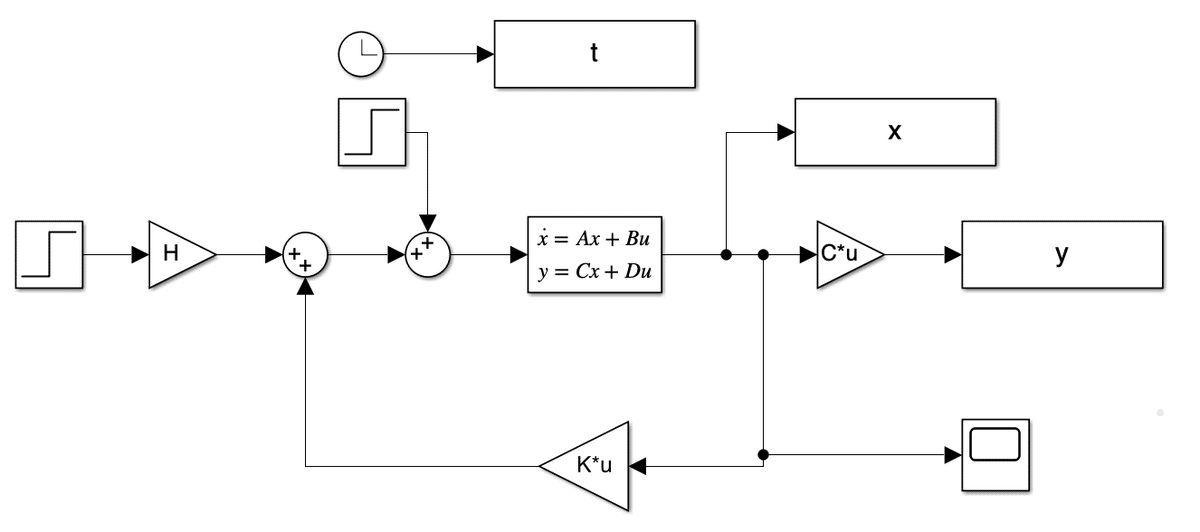
clear;
A = [0 1 0 0
     -4 -2 4 2
     0 0 0 1
     2 1 -2 -1];
B = [0 
     1 
     0  
     0 ];

C = [0 0 1 0];

p =[-1; -2; -3; -4];

K = -acker(A,B,p);

M0 = [A B;C 0];

H = [-K 1]*inv(M0)*[zeros(4,1);1];

eig(A + B*K);

x0 = zeros(4,1);

sim('simulink_sfbk');

定常偏差が残る。

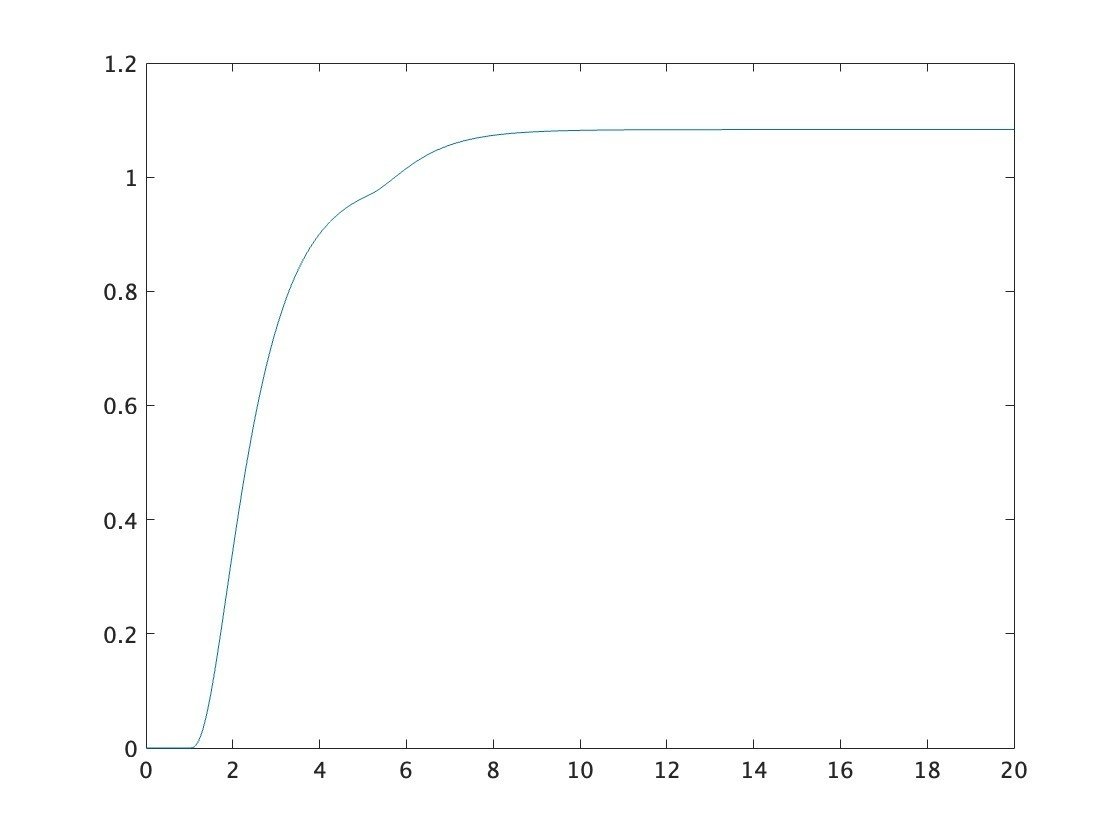
$$
\dot{\tilde{x_e(t)}}=\textbf{A}_e\tilde{\textbf{x}}_e(t)+\textbf{B}_e\tilde{\textbf{u}}(t)
$$

$$
\textbf{A}_e =\begin{bmatrix}A & O \\-C & O \end{bmatrix},\textbf{B}_e = \begin{bmatrix}B\\O \end{bmatrix} \tag{9}
$$

積分型コントローラに対しては拡大偏差システムを用いる。
拡大偏差システムは(9)によって表される。Ae, Be, pに対してアッカーマンの極配置法を適用することでKe=[K G]を得る。これを分割してそれぞれK, Gゲインとして利用する。

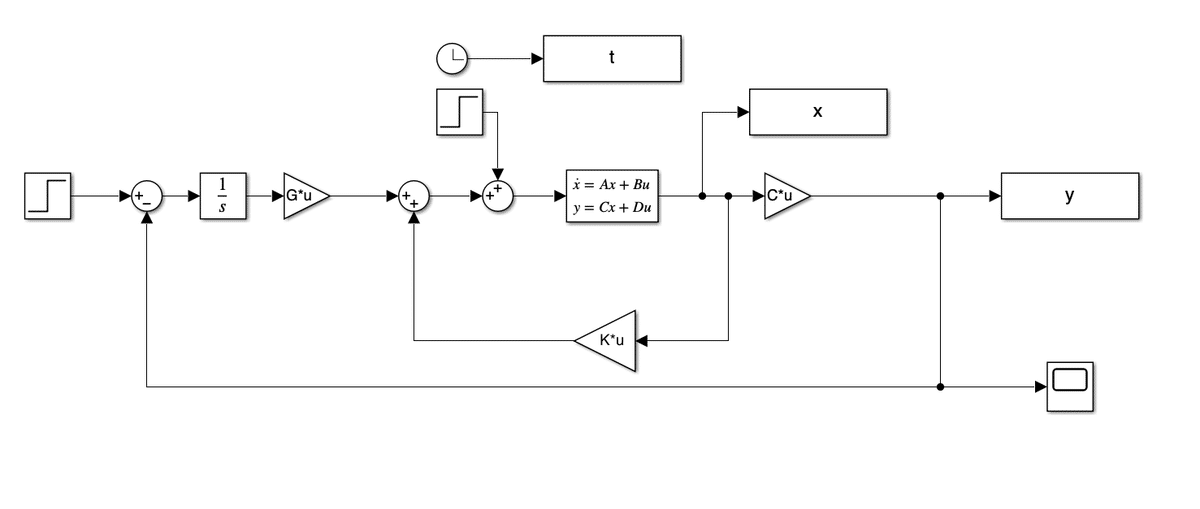
clear;
A = [0 1 0 0
     -4 -2 4 2
     0 0 0 1
     2 1 -2 -1];
B = [0 
     2 
     0  
     0 ];

C = [0 0 1 0];

Vc = ctrb(A,B);
rank(Vc)

M0 = [A B;C 0];
det(M0)

Ae = [A zeros(4,1);-C 0];

Be = [B;0];

p =[-1; -2; -3; -4;-1];

Ke = -acker(Ae,Be,p);

K = Ke(1:4);

G = Ke(5);

x0 = zeros(4,1);

eig(Ae + Be*Ke)

sim('simulink_sfbk');

定常偏差が収束している。

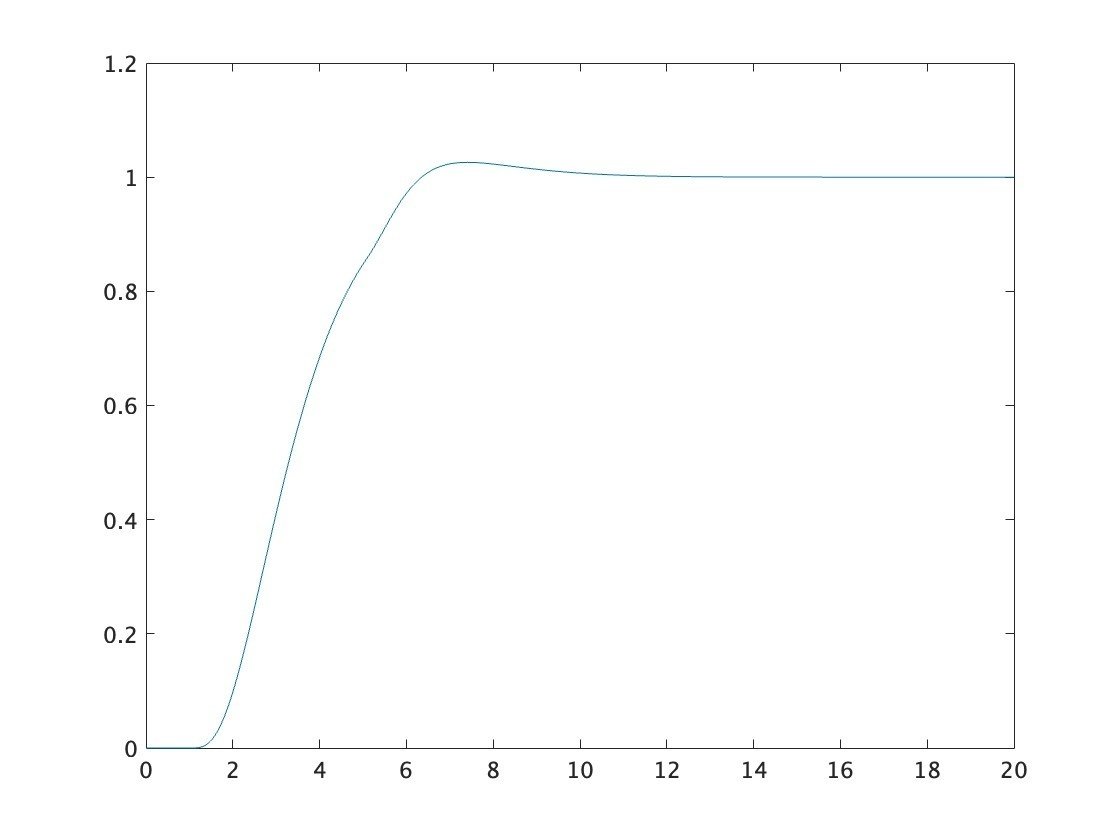
$$
\mathcal{V_o} = \begin{bmatrix} C \\ CA \\ CA^2 \\ \vdots \\ CA^{n-1} \end{bmatrix} \tag{10}
$$

Voを可観測行列という。Voのランクがn フルランクの時に可観測である。

状態方程式から単に状態量を推定する場合、以下のようになるが

$$
\dot{\hat{x}}(t) = A \hat{x}(t) + B u(t)
$$

この場合推定誤差を考えると

$$
\dot{\epsilon}(t) = A \epsilon(t)
$$

となる。この時Aが安定行列でない場合発散し、安定行列の場合収束の速さはAの固有値により決まってしまう。行列 A の固有値は制御可能ではないため推定誤差の収束特性を改善するための柔軟性が失われる。

そこで、出力信号も利用して推定誤差を補正したものを同一次元オブザーバと呼ぶ。同一次元オブザーバの式は以下のようになる。

$$
\dot{\hat{x}}(t) = A\hat{x}(t) + Bu(t) - L(\eta(t) - \hat{\eta}(t)) \\
= A\hat{x}(t) + Bu(t) - L(\eta(t) - C\hat{x}(t))
$$

ここでLはオブザーバゲインという。制御対象が安定でない場合でもA+LCが安定行列であるようにLを選べば推定誤差は以下のようになる。

$$
e(t) = e^{(A+LC)t} e_0 \rightarrow 0 \quad \text{as} \quad t \rightarrow \infty
$$

このようなLが存在することを、システムが可検出であるという。
可観測であれば可検出である。

線形システムの可観測性は可観測行列Vo 可観測性グラミアンWoにおいて

・Voがフルランクである。
・グラミアンWoが正則である。
などと等価である。

Lを適切に設定することでA+LCの固有値を任意の値に設定可能である。極配置法により設定することができる。

出力フィードバック形式のコントローラの式は以下のようになる。

$$
\dot{\hat{x}}(t) = A\hat{x}(t) + Bu(t) - L(\eta(t) - C\hat{x}(t)) \\ u(t) = K\hat{x}(t) + H y^{\text{ref}}(t)
$$

式を変形する。

$$
\dot{\hat{x}}(t) = A\hat{x}(t) + B(K\hat{x}(t) + H y^{\text{ref}}(t)) - L(\eta(t) - C\hat{x}(t))
\\ = (A + BK)\hat{x}(t) + BH y^{\text{ref}}(t) - L \eta(t) + LC \hat{x}(t)
\\ = (A + BK + LC)\hat{x}(t) - L \eta(t) + BH y^{\text{ref}}(t)
$$

式はこうなる。

$$
\dot{\hat{x}}(t) = (A + BK + LC)\hat{x}(t) - L \eta(t) + BH y^{\text{ref}}(t)
\\ u(t) = K\hat{x}(t) + H y^{\text{ref}}(t)
$$

これはコントローラなので制御対象の式と併合すると

$$
\begin{equation} \begin{bmatrix} \dot{x}(t) \\ \dot{\hat{x}}(t) \end{bmatrix} = \begin{bmatrix} A & BC_k \\ B_k C & A_k \end{bmatrix} \begin{bmatrix} x(t) \\ \hat{x}(t) \end{bmatrix} + \begin{bmatrix} B H \\ B H \end{bmatrix} y^{ref}(t) \end{equation}
$$

いいなと思ったら応援しよう！

よろしければサポートお願いします！