Pure Data biquad~　フィルターの使い方などメモ

Pure Dataについて

Pure Dataとは？ – Pure Data Japan

Pure Dataにはbiquad~というフィルターオブジェクトがあります。

biquad~は双二次フィルターという種類のフィルターオブジェクトで5つのパラメータ係数を指定することで様々な種類のフィルターとして用いることが出来ます。

双2次フィルタ

biquad~は5つの係数をリストにまとめてオブジェクトに送ることで使うことが出来ます。

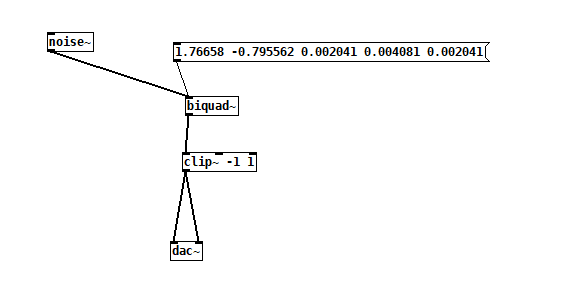
この5つのパラメータは係数と言い
左からフィードバック1~2 フィードフォワード1~3 と呼ばれます。
これをfb1,fb2,ff1,ff2,ff3とします。

係数はカットオフ周波数とサンプリング周波数、Q値から求めることが出来ます。

例えばローパスフィルターの場合　変数を次のように置くと

$$
ω= 2π \times カットオフ周波数 /サンプリング周波数\\
sinW =sin(ω) \\
cosW=cos(ω) \\
alpha = sinW / ( 2 \times Q) \\
a0= 1+ alpha \\
a1= -2 \times cosW \\
a2 = 1 - alpha \\
b0 = (1- cosW) / 2 \\
b1 = 1 - cosW \\
b2=(1-cosW)/2 \\
$$

$$
ff1 = b0/a0\\
ff2 = b1/a0\\
ff3 = b2/a0\\
fb1 = -a1/a0\\
fb2 = -a2/a0\\
$$

となります。

これをPdで書くと次のようになります。

biquad~ローパスフィルター

次にハイパスフィルタの場合は

$$
ω= 2π \times カットオフ周波数 /サンプリング周波数\\
sinW =sin(ω) \\
cosW=cos(ω) \\
alpha = sinW / ( 2 \times Q) \\
a0= 1+ alpha \\
a1= -2 \times cosW \\
a2 = 1 - alpha \\
b0 = (1 + cosW) / 2 \\
b1 = -(1 + cosW) \\
b2=(1 + cosW)/2 \\
$$

$$
ff1 = b0/a0\\
ff2 = b1/a0\\
ff3 = b2/a0\\
fb1 = -a1/a0\\
fb2 = -a2/a0\\
$$

となります。

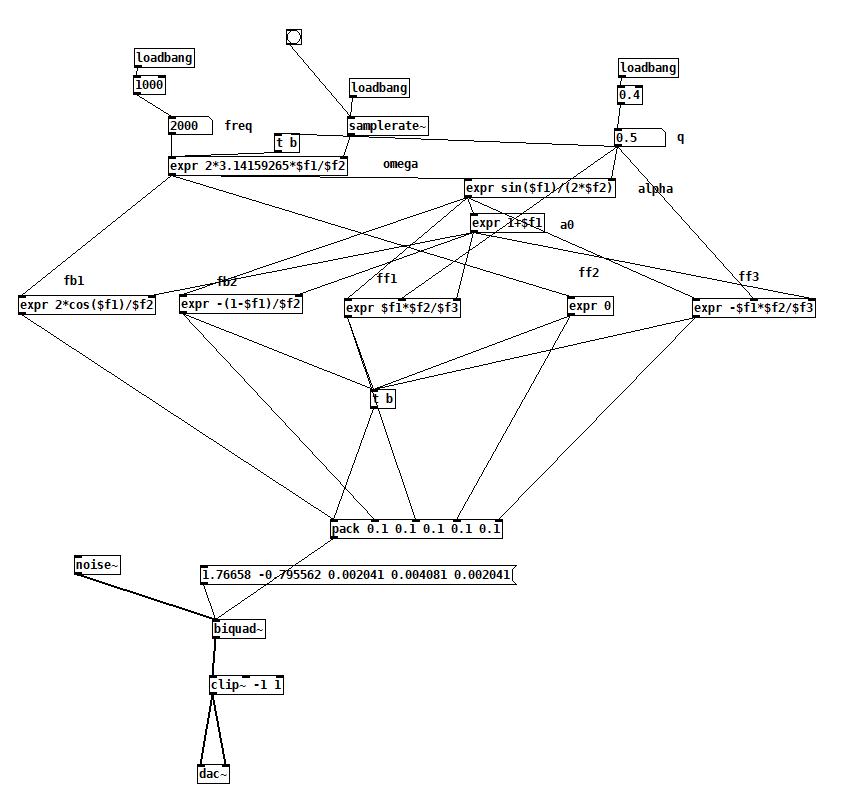
これをpdで書くと次のようになります。

ハイパスフィルタ

次にバンドパスフィルターの場合は

$$
ω= 2π \times カットオフ周波数 /サンプリング周波数\\
sinW =sin(ω) \\
cosW=cos(ω) \\
alpha = sinW /(2\times Q)) \\
a0= 1+ alpha \\
a1= -2 \times cosW \\
a2 = 1 - alpha \\
b0 = Q\times alpha \\
b1 = 0 \\
b2= -Q \times alpha \\
$$

$$
ff1 = b0/a0\\
ff2 = b1/a0\\
ff3 = b2/a0\\
fb1 = -a1/a0\\
fb2 = -a2/a0\\
$$

となります。

これをpdで書くと次のようになります。

バンドパスフィルター

onokioさん主催のレーベルBuffer Zone からアルバム:a root of sion がリリースされました。
pure dataで製作した音源から穏やかなものを中心にまとめています。
パッチも付属しています。

レーベルBuffer Zone からアルバム:Passing Sceneryがリリースされました。

maxmspで製作した音源から穏やかなものなどを中心にまとめています。
Arduinoで製作した楽器なども使っています。