
memo2
オブザーバーについて。観測量が状態変数の一部である場合を考える。
$$
\mathcal{V_o} = \begin{bmatrix} C \\ CA \\ CA^2 \\ \vdots \\ CA^{n-1} \end{bmatrix} \tag{10}
$$
Voを可観測行列という。Voのランクがn フルランクの時に可観測である。
状態方程式から単に状態量を推定する場合、以下のようになるが
$$
\dot{\hat{x}}(t) = A \hat{x}(t) + B u(t)
$$
この場合推定誤差を考えると
$$
\dot{\epsilon}(t) = A \epsilon(t)
$$
となる。この時Aが安定行列でない場合発散し、安定行列の場合収束の速さはAの固有値により決まってしまう。行列 A の固有値は制御可能ではないため推定誤差の収束特性を改善するための柔軟性が失われる。
そこで、出力信号も利用して推定誤差を補正したものを同一次元オブザーバと呼ぶ。同一次元オブザーバの式は以下のようになる。
$$
\dot{\hat{x}}(t) = A\hat{x}(t) + Bu(t) - L(\eta(t) - \hat{\eta}(t)) \\
= A\hat{x}(t) + Bu(t) - L(\eta(t) - C\hat{x}(t))
$$
ここでLはオブザーバゲインという。制御対象が安定でない場合でもA+LCが安定行列であるようにLを選べば推定誤差は以下のようになる。
$$
e(t) = e^{(A+LC)t} e_0 \rightarrow 0 \quad \text{as} \quad t \rightarrow \infty
$$
このようなLが存在することを、システムが可検出であるという。
可観測であれば可検出である。
線形システムの可観測性は可観測行列Vo 可観測性グラミアンWoにおいて
・Voがフルランクである。
・グラミアンWoが正則である。
などと等価である。
Lを適切に設定することでA+LCの固有値を任意の値に設定可能である。極配置法により設定することができる。
出力フィードバック形式のコントローラの式は以下のようになる。
$$
\dot{\hat{x}}(t) = A\hat{x}(t) + Bu(t) - L(\eta(t) - C\hat{x}(t)) \\ u(t) = K\hat{x}(t) + H y^{\text{ref}}(t)
$$
式を変形する。
$$
\dot{\hat{x}}(t) = A\hat{x}(t) + B(K\hat{x}(t) + H y^{\text{ref}}(t)) - L(\eta(t) - C\hat{x}(t))
\\ = (A + BK)\hat{x}(t) + BH y^{\text{ref}}(t) - L \eta(t) + LC \hat{x}(t)
\\ = (A + BK + LC)\hat{x}(t) - L \eta(t) + BH y^{\text{ref}}(t)
$$
式はこうなる。
$$
\dot{\hat{x}}(t) = (A + BK + LC)\hat{x}(t) - L \eta(t) + BH y^{\text{ref}}(t)
\\ u(t) = K\hat{x}(t) + H y^{\text{ref}}(t)
$$
これはコントローラなので制御対象の式と併合すると
$$
\begin{bmatrix} \dot{x}(t) \\ \dot{\hat{x}}(t) \end{bmatrix} = \begin{bmatrix} A & BC_k \\ B_k C & A_k \end{bmatrix} \begin{bmatrix} x(t) \\ \hat{x}(t) \end{bmatrix} + \begin{bmatrix} B H \\ B H \end{bmatrix} y^{ref}(t)
$$
ここで
$$
\xi_{cl}(t) = \begin{bmatrix} x(t) \\ e(t) \end{bmatrix} = \begin{bmatrix} I & 0 \\ I & -I \end{bmatrix} \begin{bmatrix} x(t) \\ \hat{x}(t) \end{bmatrix}
$$
と定義すると
$$
\xi_{cl}(t) = T_{cl} x_{cl}(t) = T_{cl} A_{cl} x_{cl}(t) + T_{cl} B_{cl} y^{ref}(t)
$$
$$
A_{cl} = T_{cl} A_{cl} T_{cl}^{-1} = \begin{bmatrix} I & 0 \\ I & -I \end{bmatrix} \begin{bmatrix} A & BK \\ 0 & A + LC \end{bmatrix} = \begin{bmatrix} A + BK & BK \\ 0 & A + LC \end{bmatrix}
\\B_{cl} = T_{cl} B_{cl} = \begin{bmatrix} BH \\ 0 \end{bmatrix}
$$
$${A_{cl}}$$ と$${\bar{A}_{cl}}$$ は相似行列となるので固有値が等しい。
$${A_{cl}}$$ の固有値が $${\bar{A}_{cl}}$$ の固有値と等しいとすると併合システムの極は$${\bar{A}_{cl}}$$の根によっても求めることができる。
すると
$$
\det(\lambda I - A_{cl}) = \left| \begin{matrix} \lambda I - (A + BK) & BK \\ 0 & \lambda I - (A + LC) \end{matrix} \right|
\\
\det(\lambda I - A_{cl}) = (\det(\lambda I - (A + BK))) (\det(\lambda I - (A + LC))) = 0
$$
となる。ここで極においてゲインKとLが分離されているので独立に設定することができる。これを分離定理という。
$${x}$$を$${\hat{x}}$$に近づけるためには$${A+L\bar{C}}$$の固有値の実部が$${A+BK}$$の固有値の実部より負の方向に大きくなるのが良い。
可観測性の判別
A = [0 -1;-1 0];
C = [0 1];
Vo = obsv(A,C)
rank(Vo)
det(Vo)clear % メモリ上の変数をすべて消去
format compact % 余分な改行を省略
% パラメータの設定
M1 = 0.5; M2 = 1;
k = 2; mu = 1;
% システム行列の定義
A = [0 1 0 0;
-k/M1 -mu/M1 k/M1 mu/M1;
0 0 0 1;
k/M2 mu/M2 -k/M2 -mu/M2];
B = [0; 1/M1; 0; 0];
C = [0 0 1 0];
% 固有値の設定
p1 = -2 + 2j; p2 = -2 - 2j;
p3 = -4 + 4j; p4 = -4 - 4j;
p = [p1 p2 p3 p4];
% 状態フィードバックゲインKの計算
K = -acker(A, B, p)
M0 = [A B;C 0];
H = [ -K 1]*inv(M0)*[zeros(4,1);1]
% オブザーバゲインHの計算
q1 = -4 + 4j; q2 = -4 - 4j;
q3 = -4 + 2j; q4 = -4 - 2j;
q = [q1 q2 q3 q4];
L = -acker(A', C', q)';
% 行列の確認と固有値の計算
disp('A + BK の固有値');
eig(A + B*K)
disp('A + LC の固有値');
eig(A + L*C)
% 併合システムの行列
Acl = [A B*K;
-L*C A + B*K + L*C];
% 併合システムの固有値の確認
disp('Acl の固有値');
eig(Acl)
N = 1.1;
M1v = N * M1; M2v = N * M2;
Av = [ 0 1 0 0;
-k/M1v -mu/M1v k/M1v mu/M1v;
0 0 0 1;
k/M2v mu/M2v -k/M2v -mu/M2v ];
Bv = [ 0; 1/M1v; 0; 0 ];
x0 = [-0.5 0 0.5 0]';同一次元オブザーバーによる出力フィードバック制御
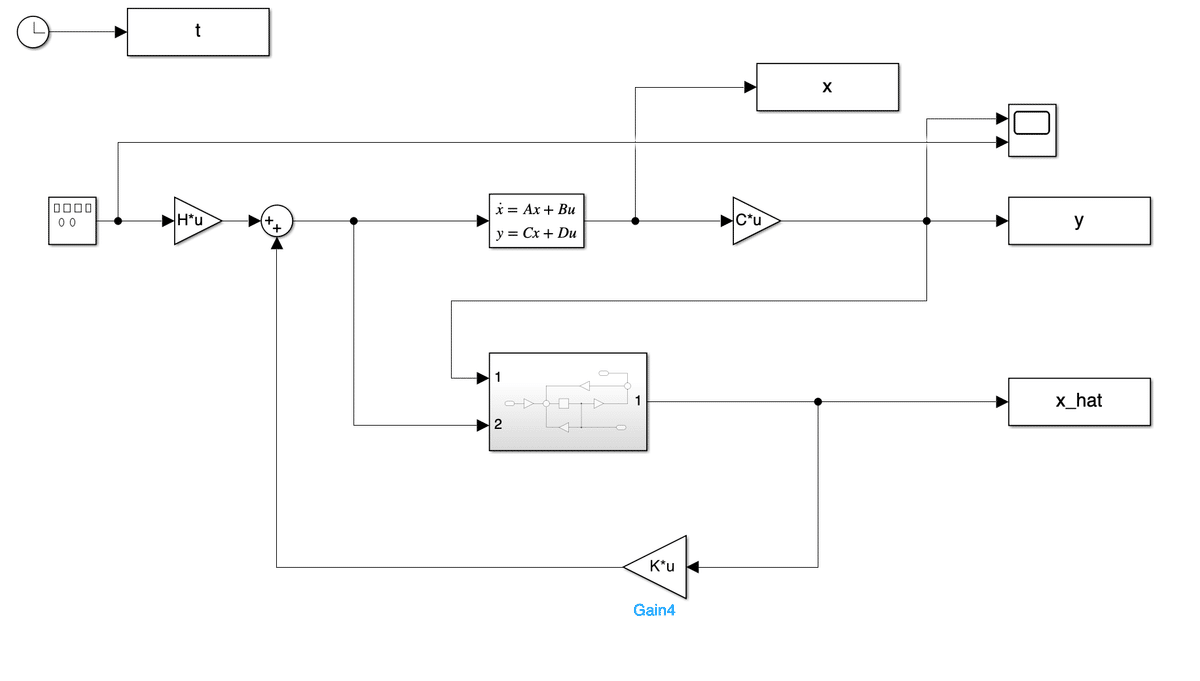
clear % メモリ上の変数をすべて消去
% パラメータの設定
M1 = 0.5; M2 = 1;
k = 2; mu = 1;
% システム行列の定義
A = [0 1 0 0;
-k/M1 -mu/M1 k/M1 mu/M1;
0 0 0 1;
k/M2 mu/M2 -k/M2 -mu/M2];
B = [0; 1/M1; 0; 0];
C = [0 0 1 0];
% 固有値の設定
p1 = -2 + 2j; p2 = -2 - 2j;
p3 = -4 + 4j; p4 = -4 - 4j;
p = [p1 p2 p3 p4];
% 状態フィードバックゲインKの計算
K = -acker(A, B, p)
M0 = [A B;C 0];
H = [ -K 1]*inv(M0)*[zeros(4,1);1]
% オブザーバゲインHの計算
q1 = -4 + 4j; q2 = -4 - 4j;
q3 = -4 + 2j; q4 = -4 - 2j;
q = [q1 q2 q3 q4];
L = -acker(A', C', q)';
% 行列の確認と固有値の計算
disp('A + BK の固有値');
eig(A + B*K)
disp('A + LC の固有値');
eig(A + L*C)
% 併合システムの行列
Acl = [A B*K;
-L*C A + B*K + L*C];
% 併合システムの固有値の確認
disp('Acl の固有値');
eig(Acl)
N = 1.3;
M1v = N * M1; M2v = N * M2;
Av = [ 0 1 0 0;
-k/M1v -mu/M1v k/M1v mu/M1v;
0 0 0 1;
k/M2v mu/M2v -k/M2v -mu/M2v ];
Bv = [ 0; 1/M1v; 0; 0 ];
x0 = [-0.5 0 0.5 0]';
sim('simulink_following_observer.slx');実際の値とオブザーバの比 1.1の場合
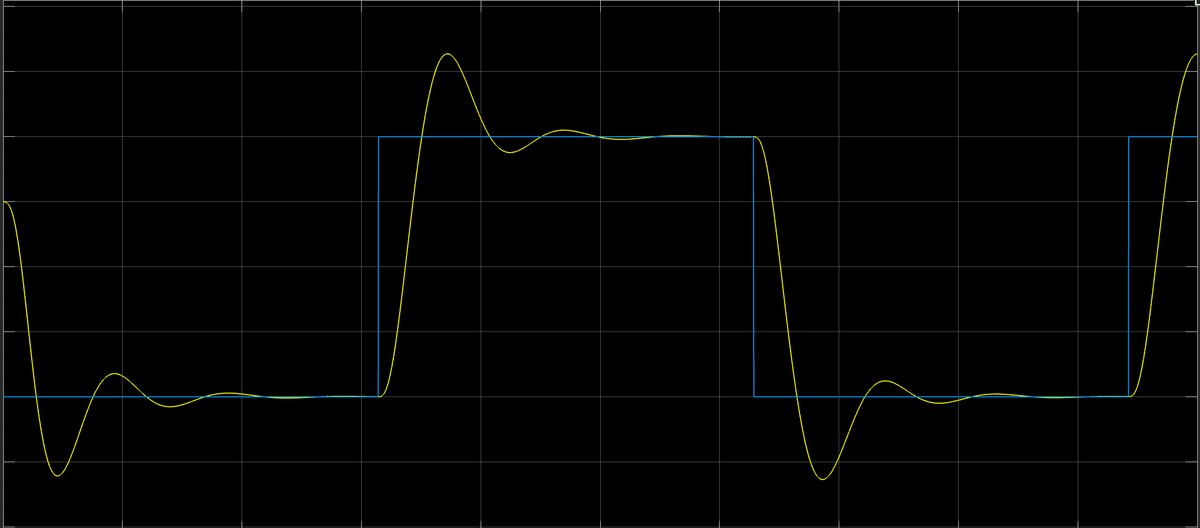
実際の値とオブザーバの比 1.3の場合
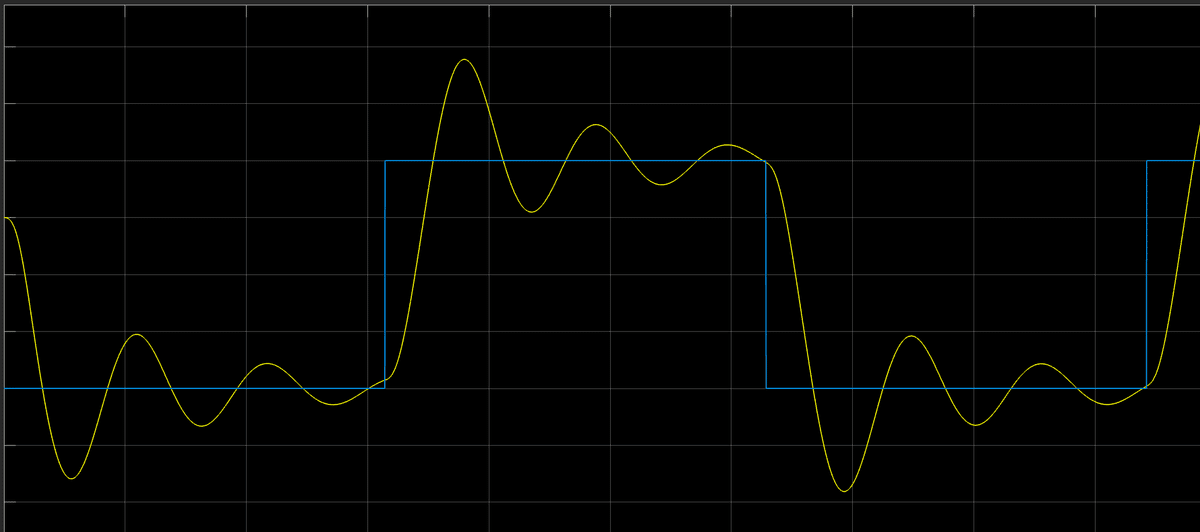
実際の値と差がある場合は追従性が悪化している。
参考資料
いいなと思ったら応援しよう!

