Pythonで機械学習 (性能評価指標)
2019年、明けましておめでとうございます。今年はnoteを継続して書き続け、なんとか100件は書きたいと思っています。2019年1本目のネタは 機械学習の性能評価指標について勉強したので、ここにアウトプットしてみます。
・前回のトレーニングデータを用いて構築したモデルがどれほど良いものかを評価する指標があり、それは性能評価指標と言われる。
・機械学習では混合行列の正解率( TP+TN / FP + FN + TP + TN) を使わない。これは、データに偏りがある状態で使うと、正解率が高くなり、モデルによっては良くない判断となるためです。
・そこで、機械学習では、適合率(precision)と再現率(recall)、F値(適合率と再現率の両方を組み合わせた平均)を用いる。





検証1
以下の例では、患者1000人の癌検診の診断結果を混合行列にしたもの。
・癌だろうと診断した50人の中で実際に癌だったのは30人 (TP)
・癌だろうと診断した50人の中で癌ではなかったのは20人(FP)
・癌ではないと診断した950人の中で実際は癌だったのは12人(FN)
・癌ではないと診断した950人の中で癌じゃなかったのは938人(FP)

この場合の適合率、再現率、F値はそれぞれ以下のように求められ、0〜1の範囲で1に近いほうが性能が良いことを示している。
適合率(Precision) = TP / (TP + FP) = 30 / (30 + 20) = 60%
再現率(Recall) = TP / (TP + FN) = 30 / (30 + 12) = 71%
F値= 2 * ( precision * recall ) / (precision + recall) = 2 * 60 * 71 / 60 + 71 = 65%
※混合行列の正解率では、 (TP + TN) / (FP + FN + TP + TN) = 30 + 938 / 20 + 12 + 30 + 938 = 97% となり、癌なのに癌ではないと誤診された人が12人、癌じゃないのに癌と誤診された人が20人もいるのに、正解率(97%)は合致する値ではない。
検証2
同じ検査で結果が異なる例。上の検証1と比較して直感的にも良くない結果とわかるが、実際に計算してみても悪い数字が出る。
・癌だろうと診断した120人の中で実際に癌だったのは30人 (TP)
・癌だろうと診断した120人の中で癌ではなかったのは90人(FP)
・癌ではないと診断した880人の中で実際は癌だったのは40人(FN)
・癌ではないと診断した880人の中で癌じゃなかったのは840人(FP)

適合率(Precision) = TP / (TP + FP) = 30 / (30 + 90) = 25%
再現率(Recall) = TP / (TP + FN) = 30 / (30 + 40) = 43%
F値= 2 * ( precision * recall ) / (precision + recall) = 2 * 25 * 43 / 25 + 43 = 32%
検証3
適合率と再現率はトレードオフなので、どちらかを上げようと重視すればもう一方の値は下がる
・癌だろうと診断した200人の中で実際に癌だったのは65人 (TP)
・癌だろうと診断した200人の中で癌ではなかったのは135人(FP)
・癌ではないと診断した800人の中で実際は癌だったのは5人(FN)
・癌ではないと診断した800人の中で癌じゃなかったのは795人(FP)
適合率(Precision) = TP / (TP + FP) = 65 / (65 + 135) = 33%
再現率(Recall) = TP / (TP + FN) = 65 / (65 + 5) = 86%
検証4
検証3と同じ結果だが、検証3よりも厳し目の検査を行った結果。(癌であると診断した人が少なめ)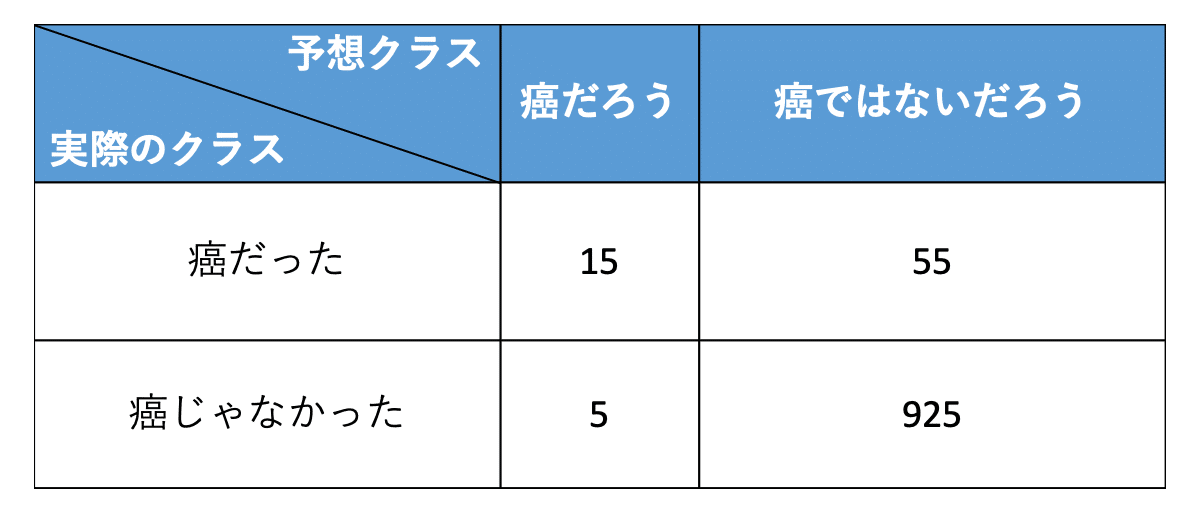
適合率(Precision) = TP / (TP + FP) = 15 / (15 + 5) = 75%
再現率(Recall) = TP / (TP + FN) = 15 / (15 + 55) = 20%
結果、適合率は上がったが、再現率は下がった。
上記の癌診断の場合は、癌を見逃すと人の命に関わるので、甘めの検査、つまり再現率を重視した方が良いケース。ただし、例えば個人の購買履歴やクリックした広告を分析してレコメンドするサービスでは、興味のない広告を流す可能性もあるので、無駄打ちはリスクは避けたい。そういった場合は厳し目の評価、つまり適合性を重視した方が良い。
性能評価指標をpythonで実装
# 適合率算出ライブラリ
from sklearn.metrics import precision_score
# 再現率算出ライブラリ、F値算出ライブラリ
from sklearn.metrics import recall_score, f1_score
# 1 = 陽、0 = 陰
y_true = [1,1,1,0,0,0]
y_pred = [0,1,1,0,0,0]
# TP=2 FP=0, FN=3, TN=1
#
# [ 2 1 ]
# [ 0 3 ]
#preciscion, recall, f1 score関数は 1=陽、0=陰として計算している
print("適合率、再現率、F値")
print("===================")
print("Precision: %.3f" % precision_score(y_true, y_pred))
print("Recall: %.3f" % recall_score(y_true, y_pred))
#print("F1: %.3f" % f1_score(y_true, y_pred))
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
#f1_score()でも計算できるが、ここでは計算式にあてはめてみる
f1_score = 2 * (precision * recall) / (precision + recall)
print("F1: %.3f" % f1_score)実行結果
適合率、再現率、F値
===================
Precision: 1.000
Recall: 0.667
F1: 0.800いいなと思ったら応援しよう!

