繰り下がりは「お金」で覚える

先月、Twitterで「さくらんぼ計算」が話題になっていた。「さくらんぼ計算」は小学一年生の「繰り上がり」と「繰り下がり」の計算の教え方の一つで、多くの学校で採用されているものだ。

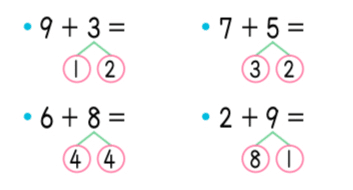
上の写真のとおり、「10の補数」を作ったりするために数を分解し、さくらんぼのような二つの円に書くという方法なのだが、この「さくらんぼ計算」が理解できないお子さんについての悩みや、繰り上がり・繰り下がりの概念をすでに理解していても、さくらんぼの中にわざわざ数字を書かされることへの批判がフツフツとタイムラインを沸騰させていたのだ。

どんな教育法でも、すべてのお子さんに通用するものはない。せいぜい6割に通じれば「よい教育法」と言われるレベルだ。たぶん「さくらんぼ計算」も、そんな教育法の一つだと思う。

でも、残りの4割の子はどうすんのよ……と思ってしまうのは、私もその「4割」に入っていた気がするからだ。

私は学生時代、算数や数学がとても苦手だった。その苦手は小学校一年から始まっていて、きっかけは繰り下がりの計算だったと思う。

覚えているのは、先生が「11－4＝」と大きく黒板に書いて、繰り下がりの計算を教えようとしたときのことだ。

「まずは一の位どうしを引き算しなけらばいけないけれど、1から4は引けないね。なので、十の位の10を借りてきましょう」

借りる？ 借りるってことは、いつか返さなくちゃいけないってこと？？？？――生まれつき理屈っぽく、言葉へのこだわりが強かった6歳の私はそう考えたのだ。

借りた10から4を引いてしまっては6しか残らない。それで10をどう返せというのか、と。「あと10日待ってください。必ず用意します」と、土下座をすればいいのか。それとも、ほかの計算式からこっそり10をパクってくるべきなのか――。

そんな調子で、九九も「どうして3×3が9で、4×3が12だってわかるんだろう？ この『×』って何？」と考えることに集中してしまい、なかなか覚えられなかった。

しかし、「10を『1が10個』として考えればいいんだ！」「3×3は、3を3回足すことと同じだ！」という理屈に気づいた瞬間に、繰り上がりの計算も九九も、ある程度できるようになった。

つまり理屈っぽい私は、理屈がわからないものをそのまま丸覚えするのが苦手なんだろう。得意だった国語でも、文章中の言葉であれば丸ごと覚えることができるのに、漢字をひたすら暗記するのは苦手だった。

そんな私の理屈っぽさを見込んでか、昨年、知人から娘さんのAちゃんについて、こんな相談を受けた。

「うちの子、算数が苦手で。特に繰り下がりの引き算がねぇ……」

Aちゃんのことは小さい頃から知っていた。とてもしっかりした女の子で、本が大好きで、自分で物語を作っては聞かせてくれた。そして、そんなところが、小さい頃の私に似ているなぁと思っていた。

だとするると、もしや……。
私は知人に、そっと訊いてみた。

「もしかしてAちゃんは、繰り下がりの計算で『十の位の10を借りてくる』って説明に引っかかってない？」
「そう！ そうなの！ 『借りてきた10は返さなくちゃいけないんでしょ？』とか言うのよ！」

まさにビンゴ。やはりAちゃんは私と同じタイプだった。

「大切なのは、『借りる』みたいな無駄な言葉を使わないで『十の位の数を一の位の数に戻す』という理屈を教えることだよ」

理屈っぽい子どもの先輩として、私は知人にこんなアドバイスをした。

「まず、紙に繰り下がりの計算式を書くじゃない？ そして引かれる数のほうに、対応する10円玉と1円玉を置く」

「で、一の位どうしで引き算ができないときは、10円玉――つまり十の位の数を、1円玉に戻す。いわゆる『両替』ね」

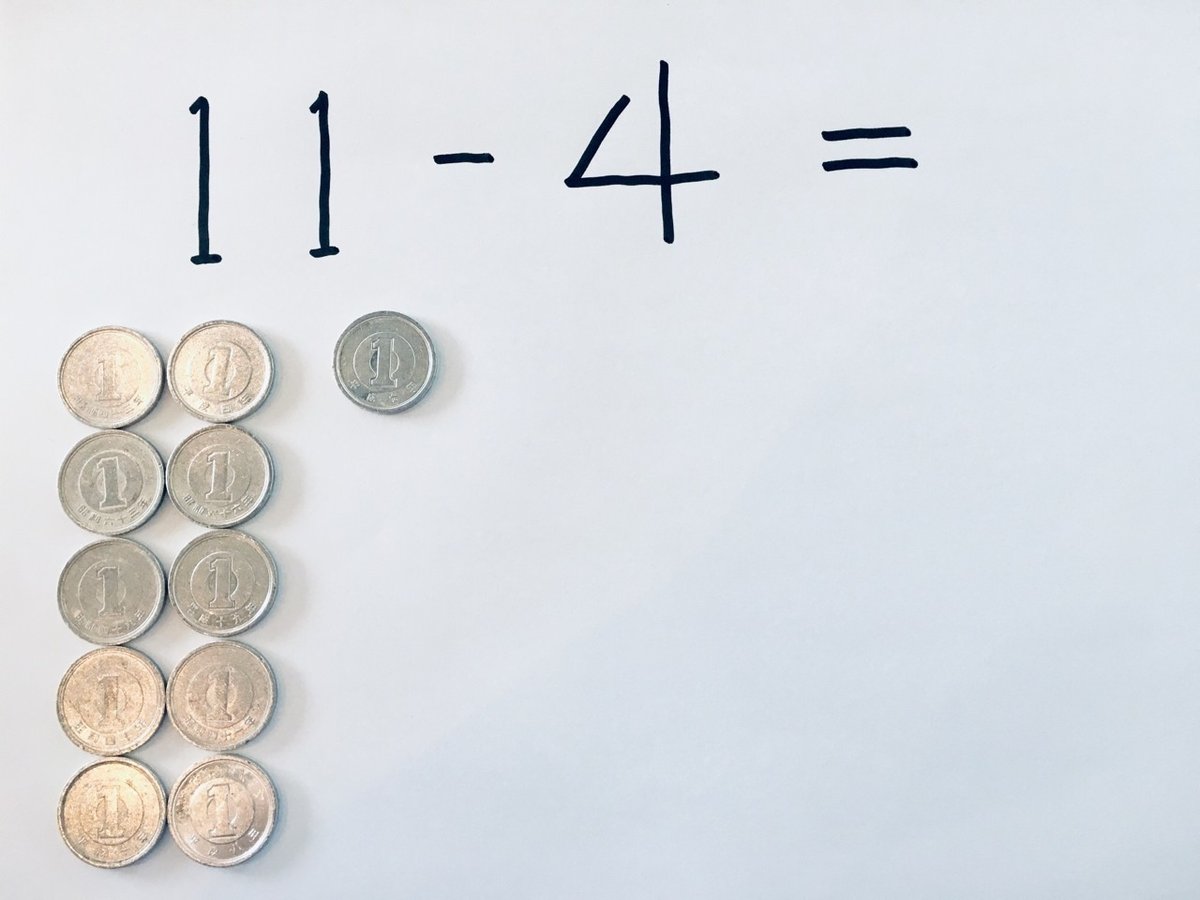
「そして、10円玉1枚から1円玉10枚になったところから、引く数の分（ここでは4）だけ、1円玉を取る」

「あとは、残った6枚と、一の位にもともとあった1枚を足して、答えを出す」

Aちゃんは、この方法のおかげで繰り下がりの計算が解けるようになり、「繰り上がりよりも得意！」とまで言ってくれるようになったらしい。

これは理屈っぽい私が、同じく理屈っぽい息子に教えていた方法で、ポイントはただ一つ。「本当の硬貨でやること」だ。おもちゃの硬貨でやると、なぜかあまり理解してもらえない。不思議だ。不思議だけど、その理屈はなんとなくわかる。

どんなに難しい勉強であっても、実際の日常生活とくっつき、活用できるものであれば、人間はある程度理解できるってことだろう。いわゆる「勉強のできない子」が、のちにお金の計算がしっかりできる大人になったりするのも、そこらへんが理由なんじゃないかなーと思っている。