場合の数(順列と組合せ)｜SPI3非言語対策

■和の法則と積の法則

場合の数や確率において、値が複数個出てきたとき、たし算(和の法則)をするかかけ算(積の法則)の判別法は、

◆たし算(和の法則)
それらが同時に起こらないときや場合分けをして求めた値のときは、それらのたし算で求める。

◆かけ算(積の法則)
それらが同時に起こるときや連続して起こるときは、それらのかけ算で求める。

■順列と組合せ

◆順列の求め方
例題１の「5文字から3文字を選んで一列に並べる」のように、選んで並べることを順列という。
求め方は、
① 並べるものの数だけ枠を作る。
② 左から順にそれぞれの枠に入れる場合の数を考える。
③ 連続して起こっているので、かけ算をして求める。

◆組合せの求め方
例題２の「5文字から3文字を選ぶ」のように、選ぶだけを組合せという。
求め方は、組合せの公式Ｃを用いて解く。

例えば、

このように計算する。

■例題１【場合の数(順列と組合せ)】

━━━━━━━━━━━━━━━━━━━━━
◆例題：a、b、c、d、e の5文字から3文字を選んで一列に並べる方法は何通りか？
━━━━━━━━━━━━━━━━━━━━━
◆例題解説
この問題では3文字を一列に並べるので、次のように①から③までの枠を作ると、

左側の①には、a、b、c、d、e の5文字から1文字を選んで入れるので、5通りである。
次に、②には①で入れた文字以外の4文字から選ばるので、4通りである。
③は、残りの3文字から選ばれるので3通りとなる。

よって、①→②→③と連続して考えているのでかけ算をしていくと、

したがって、答えは 60通り となる。

■例題２【場合の数(順列と組合せ)】

━━━━━━━━━━━━━━━━━━━━━
◆例題：a、b、c、d、e の5文字から3文字を選ぶ方法は何通りか？
━━━━━━━━━━━━━━━━━━━━━
◆例題解説
この問題では選ぶだけであるので、組合せとなる。
5文字から3文字を選ぶ方法は ₅Ｃ₃ となり、
・分子は5から3つの数字のかけ算
・分母は3から3つの数字のかけ算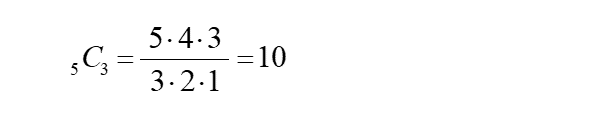

したがって、答えは 10通り となる。