判定偏差値と合格者平均偏差値の関係④ 大受/高受/中受の比較分析
大学受験・高校受験・中学受験の判定偏差値と合格者平均偏差値の関係について、過去3回にわたって記事を書いています。このシリーズの最後の記事として、今回はその比較分析を行います。
0. まとめ
同じ判定偏差値の学校でも、模試によって受験者の学力分布が異なる。判定偏差値の設定幅と整合するモデルを作ると、駿台中学生テスト(高校受験)>駿台全国模試(大学受験)>合格力判定サピックスオープン(中学受験)の順で受験者の分布が広い
その結果、同じ判定偏差値の学校でも合格者平均偏差値は、合格力判定サピックスオープン(中学受験)>駿台全国模試(大学受験)>駿台中学生テスト(高校受験)の順で高くなる。
こうした差異があるため、異なる模試間で学校の学力を判定偏差値で比較するのは不適切。
1. 判定偏差値の幅
模試によって(さらに学校によって)、A判定とB判定、B判定とC判定などの判定の幅は異なっていました。一覧にするとこのようになります。いずれもインターネットで入手できたサンプルの集計値です。

合格率80%偏差値を基準としたマイナス幅を記載していますが、模試によって判定偏差値が設定されている合格率が異なります。そのため、差分を等比として推定してみます。

このような判定幅の設定の場合、合格率80%の判定偏差値が60の学校で、判定偏差値がそれぞれいくつになるか計算したのがこの表です。
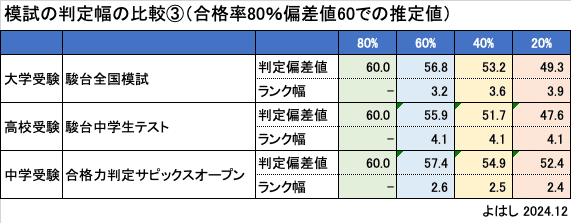
判定のランク幅は、駿台中学生テスト(高校受験)>駿台全国模試(大学受験)>合格力判定サピックスオープン(中学受験)と推定されています。そのため、60%/40%/20%合格率の判定偏差値はこの逆となって、合格力判定サピックスオープン(中学受験)>駿台全国模試(大学受験)>駿台中学生テスト(高校受験)となるようです。
2. 判定偏差値と合格者平均偏差値の差
判定偏差値と合格者平均偏差値の差は、これまでの分析結果を一覧にすると、このようになります。なお、それぞれの模試の偏差値55〜70程度で倍率3倍前後の学校が基準です。80%偏差値は合格率80%の判定偏差値で、模試によってA判定や確実圏と呼ばれています。
駿台全国模試(大学受験)
合格者平均偏差値=80%偏差値 - 4.0
※難関国立10大学算術平均
合格者平均偏差値=80%偏差値 - 3.6
※模試判定モデル・倍率3.0倍の推定値駿台中学生テスト(高校受験)
合格者平均偏差値=80%偏差値 - 6.1
※合否分布のサンプル47校の平均値合格力判定サピックスオープン(中学受験)
合格者平均偏差値=80%偏差値 - 1.3
※合否分布のサンプル4校の平均値
合格者平均偏差値=80%偏差値 - 0.7
※志望分布サンプル38校からの推定値
なお、合格力判定サピックスオープンの志望分布サンプルから推定される合格者ピークは、実際の合否分布サンプルより+1〜2ほど上振れしていることが確認されています。そのため、この上振れを補正すると、「合格者平均偏差値=80%偏差値 - 2.7」まで広がる可能性あります。
この点も考慮してと、概数にすると次の計算式になります。合格率80%偏差値と合格者平均偏差値の差は、合格力判定サピックスオープンで最も狭く(2)、駿台中学生テストで最も広い(6)ことがわかります。
駿台全国模試(大学受験)
合格者平均偏差値=80%偏差値 - 4駿台中学生テスト(高校受験)
合格者平均偏差値=80%偏差値 - 6合格力判定サピックスオープン(中学受験)
合格者平均偏差値=80%偏差値 - 2
3. 模試ごとの分布の推定
上記のように、大学受験/高校受験/中学受験のそれぞれを代表する難関模試では、判定偏差値の幅や合格者平均との差が異なるようです。この違いを生む要因として、同じ判定偏差値の学校に対する受験者の学力分布を分析していきます。
学力分布をシミュレーションする際、80%偏差値が60で倍率3倍の学校を想定し、合格者と不合格者はそれぞれ正規分布すると仮定します。この場合、合格者平均はこれまでの分析で算定した80%偏差値との差を用いて、駿台全国模試では56、駿台中学生テストでは54、合格力判定サピックスオープンでは58となります。
また、この時に偏差値60で合格率80%になるように、不合格者平均とそれぞれの分布の標準偏差(共通)を計算してます。一覧にすると、この表になります。

この設定値で、合格者と不合格者の分布をグラフを作ります。上から大学受験、高校受験、中学受験です。



80%判定偏差値が同じ60であっても、合格者の分布が異なることが見て取れます。合格者と不合格者の分布が違うことから、20%・40%・60%の判定偏差値も模試によって違う位置に来ていることがわかります。
それぞれで推定された20%・40%・60%の偏差値を一覧にしたのがこの表です。サンプルの平均判定幅から計算した判定偏差値との差も記載していますが、概ね近い数字になっており、モデルとしては実態にそれなりに近いものと考えられます。

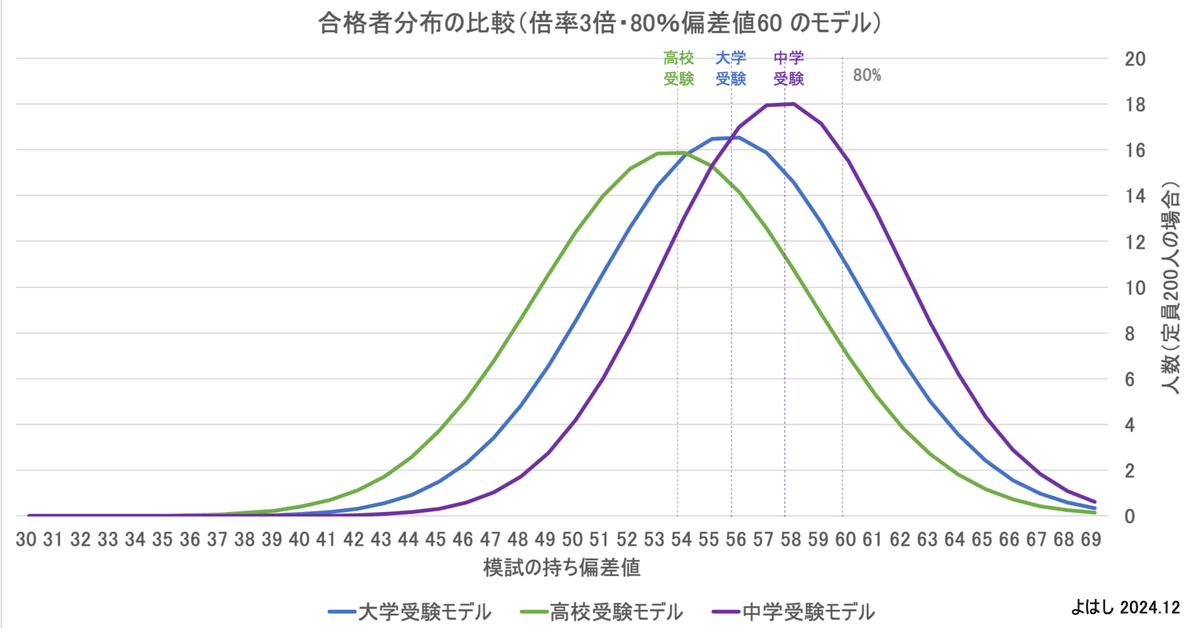
このシミュレーションで得られた3つの模試の合格者分布を一つのグラフに重ね合わせると、このようになります。
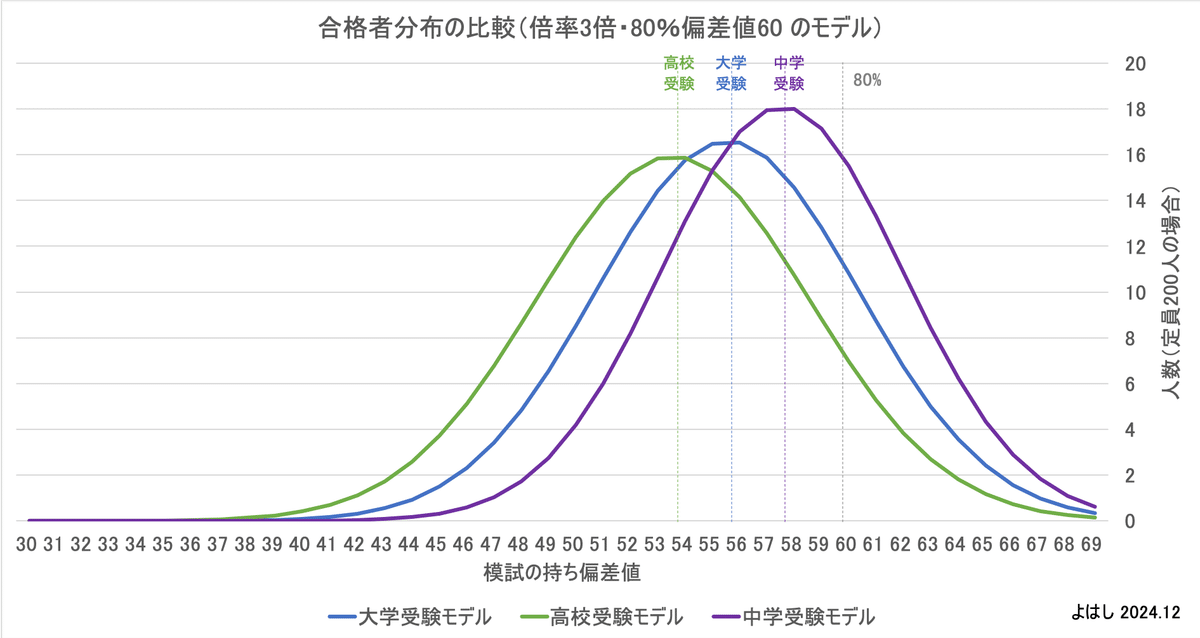
また、合格者分布と不合格者分布を合計した受験者の分布もグラフで見てみます。合格者と不合格者をそれぞれ正規分布にしたため、受験者は正規分布にはなっていません。

4. 逆方向からの考察
ここまでは、サンプルや理論値から計算された判定偏差値の幅や合格者平均偏差値から、同じ判定偏差値の学校に対する合格者分布と受験者分布をシミュレーションしてきました。ただ、本来は逆です。
同じ判定偏差値の学校でも、模試によって志望者(受験者)の学力分布が異なり、その結果、合格者分布と合格者平均偏差値が異なるはずです。また、その合格者分布から判定偏差値が統計的に計算された結果として、判定偏差値の幅も異なるはずです。
このように逆方向から考察すると、次のメカニズムで模試ごとの違いが生まれていると考えられます。
同じ80%判定偏差値の学校に対する受験者の分布は、駿台中学生テスト(高校受験)>駿台全国模試(大学受験)>合格力判定サピックスオープン(中学受験)の順に広い
そのため、同じ80%判定偏差値(例:60)の学校に対する受験者の平均偏差値は、駿台中学生テスト(50)<駿台全国模試(52)<合格力判定サピックスオープン(53)の順に低くなる
こうした受験者が同じ80%判定偏差値(例:60)の学校を受験すると、合格者の分布は、偏差値が低い方から順番に、駿台中学生テスト、駿台全国模試、合格力判定サピックスオープンの順に並ぶ
また、受験者の分布の広さの違いから、合格者の分布も駿台中学生テスト>駿台全国模試>合格力判定サピックスオープンの順に広くなり、これが20%・40%・60%の判定偏差値の違うを生む
これらの結果、同じ80%判定偏差値(例:60)の学校でも、合格者平均偏差値は、駿台中学生テスト(54)<駿台全国模試(56)<合格力判定サピックスオープン(58)となる
5. 最後に
今回の比較分析により、駿台全国模試と駿台中学生テストと合格力判定サピックスオープンにおいて、同じ合格80%偏差値に対する受験者や合格者の分布が違うことがわかりました。この分布の違いが、模試ごとの合格80%偏差値と合格者平均偏差値の差の違いを生んでいます。
逆に言えば、異なる模試の判定偏差値を用いて、学校の学力を比較するのは見誤るということです。これは同じ受験タイミングにおける異なる模試(例:大学受験の駿台全国模試と全統記述模試)でも同様と考えられます。
おそらく、最も比較基準として適切なのは合格者平均偏差値ですが、これは一般には公表されていません(一部の内部生向けの資料には記載されている模様)。合格者平均偏差値が入手できない場合は、模試ごとに合格80%偏差値からの差で推定して比較するのが次善の策と言えます。
これが今回の分析の結論です。
