
東大入試をもう一度やったら半数が入れ替わるのか? (大学の合格最下位学力の統計分析④)【全面改定版】
趣味の統計分析で、最近は共通テストリサーチのデータを使って、大学の合格最下位学力の推定を行っています。
これまでの分析結果を見ると、理三の合格最下位の推定は、共通テストリサーチのデータを用いた分析では精度があまり高くなさそうでした。今後、東大の科類の比較分析を行う予定ですが、その際には共通テストリサーチだけでなく、いくつかの合格者数の推定方法を組み合わせる必要がありそうです。
こうした状況の中、駿台全国模試の判定を使って合格者数の推定モデルを作りました。そのモデルを使うトライアルとして、表題の「東大入試をもう一度やったら半数が入れ替わる」という言説の検証も行ってみます。
駿台全国模試の判定偏差値の基準設定を私が勘違いしていたことが判明しました。そのため、モデルを再構築し、記事内容を全面改定しました。
ただし、数字は以前のものから変わっていますが、結論は変わっていません。(2024.10.19)
0. まとめ
倍率が2.5倍の大学(東大理一など)で、受験者におけるA判定:B判定:C判定:D判定の比率がおおよそ1:1:2:2であれば、合格者の約半分がA判定とB判定、残り半分がC判定とD判定となる。
このような分布となる東大合格者にもう一度入試を行った場合、再合格の比率(再合格率)は、理一では53%、文一・文二・文三では52%、理二・理三では51%となる。
逆に見ると、もう一度東大入試を行った場合に入れ替わる比率は、47〜49%である。そのため、「東大合格者にもう一度入試を行ったら半数が入れ替わる」というのは、概ね正しいと言える。
一般化すると、再合格率は判定分布と倍率の関数であり、「大学入試に限らず、高校入試や中学入試でも、倍率が3.5〜4.0倍を超えると、合格者にもう一度入試を行ったら半数以上が入れ替わる(再合格50%未満)」と言える。
1. 駿台全国模試の判定での合格者数推定ロジック
判定基準の見直しの過程で、駿台模試判定から合格者数などを推定するモデルを再構築しています。詳しくはこちらをご覧下さい。なお、この記事の分析にある通り、東大受験者の判定のA:B:C:Dの比率は、1.0:0.8:1.9:1.9とし、E判定の比率は倍率から逆算した残りとします。
2. 東大合格者はどれくらい入れ変わるのか?
「東大合格者にもう一度入試をやったら半数が入れ替わる」というのは、ネットの記事を見ると、開成高校の先生や東大の入試委員会が言ったようです。この仮説に対して、上記の合格者推定ロジックで検証してみます。
①理一
まずは、最大受験者数の理一から分析します。理一の倍率2.5倍です。この倍率において、A:B:C:Dの比率が1.0:0.8:1.9:1.9であれば、東大理一合格者の受験時の判定の比率は、A:B:C:D:E=41:32:79:78:20となります。
それぞれに合格可能性を乗じた理論上の合格者の構成は、33%:19%:32%:16%:1%となります。この時、A判定とB判定からの合格者は33+19=52%なので、合格者の半数以上がB判定以上です。逆にD判定以下からの合格者も16+1=17%=6人に1人います。
さて、この東大理一合格者が東大理一の入試をもう一度受験する場合、再受験者の判定の比率もA:B:C:D:E=33%:19%:32%:16%:1%となります。これに合格可能性を乗算したのが右側の緑の部分で、1回目の合格者(定員100%)に対する再合格者の比率は、26%+11%+13%+3%+0%=53%となります。。

最初の合格者に対する再受験の合格者は53%なので、2人に1人しか再合格できていません。逆に言えば、東大理一受験をもう一度行うと、2人に1人が不合格で入れ替わっていることになります。
それでは、他の科類もシミュレーションしていきましょう。
②文一・文二・文三
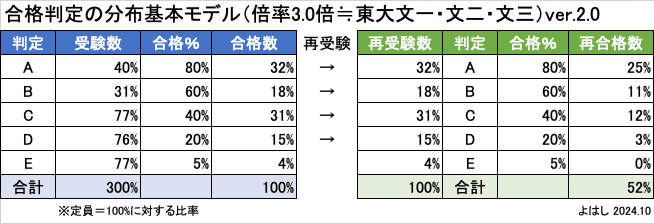
文一・文二・文三の倍率は約3.0倍です。この推定モデルでは、倍率が増えると残差のE判定が増えるので、もう一度入試を行った時の再合格率は52%に低下します。文一・文二・文三では、合格者の48%が入れ替わることになります。
③理二・理三
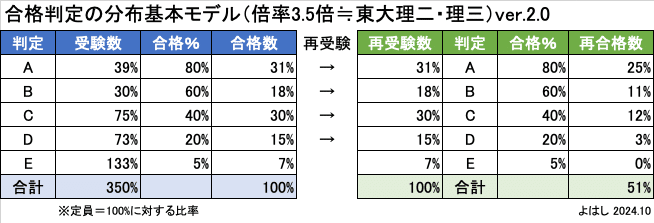
理二・理三は倍率が約3.5倍なので、推定モデルの仕組み上、E判定の受験者が大半になります。そのため、理二・理三では再合格率はもう少し下がって、51%となります。実際にはE判定にここまで偏ることはなく、C〜E判定を行き来している受験者のチャレンジが多いのだろうと思います。
これらは、駿台全国模試の判定から簡易的に作った推定モデルですが、「東大入試をもう一度やったら半数が入れ替わる」というのは、概ね正しそうだということがわかりました。
3. 再合格率の一般化
この推定ロジックでは、判定比率と倍率で再合格率を計算しています。そのため、A〜E判定の比率が同じであれば、どこの大学の入試であっても倍率を変数として再合格率は決まるはずです。
駿台模試判定モデルに含まれる5つのモデル(東大・国立一般・早稲田・慶應・私立一般)について、倍率を変えると再合格率がどう変わるかを計算したのがこの表です。なお、東大は1次試験で足きりがあるので、3.5倍を超えることはありませんが、計算上の数値として3.5倍以降も記載しています。

大学別のモデル=判定分布によって凸凹はありますが、倍率3.5倍を超えたあたりから再合格率が50%を下回り始めます。そして、倍率4倍を超えるとどのモデルでも再合格率が50%未満となり、半数以上が不合格になるようです。
そして、これは判定分布と倍率からの計算のため、大学受験に限らずに、同じような分布であれば、高校受験や中学受験でも同様のことが言えると考えられます。
4. 最後に
今回は「東大合格者にもう一度入試を行ったら、半数が入れ替わる」という命題の検証を行いました。次回もこの推定モデルを使って、いくつかの命題について考察を行ってみます。具体的には次の命題です。
筑波大駒場中学の合格は運なのか?
都立高校受験でA判定なら合格率100%なのか?
医学部のボーダー偏差値はなぜ高いのか?
