【R7年度入試】 都立•進学指導重点校の合格最低点の統計予測モデル 〜日比谷・西・国立・戸山・立川・青山・八王子東〜
※この記事は2025年2月21日実施の令和7年度入試に関する予測です。
子供の都立高校受験を機に、進学指導重点校の合格最低点の統計予測モデルの記事を何本か書いています。このシリーズは、私の記事の中で最も読んでいただいている記事になります。そこで、今年(R7年度入試)も進学指導重点校の合格最低点の統計予測を行いましたので、記事にしてみます。
本記事で扱う合格最低点は、ESAT-Jも含む1020点満点における点数となります。また、3教科合計の受検者平均点(以下、3教科平均点)は各教科の受検者平均点の単純合算値です。
なお、この記事の内容は合格最低点や合格可能性を断定的に予想するものではありません。あくまで、今年の受検者倍率なら、過去6年の3教科平均点を元にすると、統計的にはこのくらいの合格最低点やこの合格可能性になるはずという予測値です。あくまでも参考値として、見てください。
0. まとめ
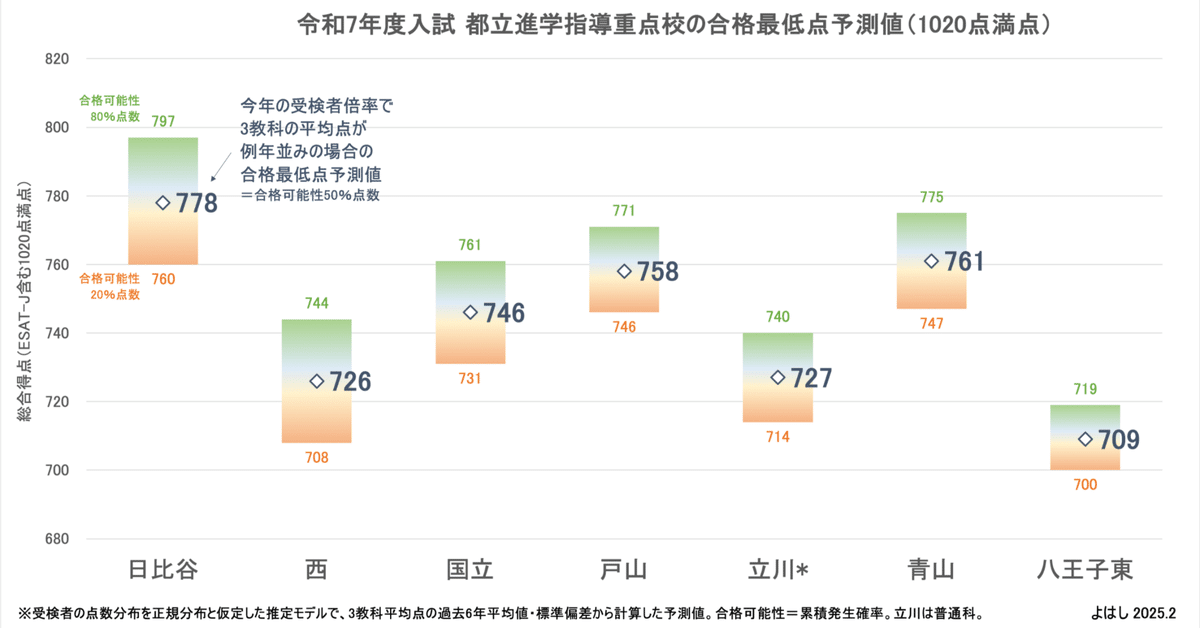
当日に発表された受検者倍率に基づくと、今年のテストの難易度(受験者平均点)が例年並みであれば、都立高校・進学指導重点校の令和7年度入試における合格最低点の予測値は以下の点数となります。
統計的には、この点数は合格可能性(発生確率)50%の点数です。あわせて、合格可能性80%の点数も記載しています。
◆合格最低点の予測値(例年並みの難易度の場合)
=合格可能性50%の点数
日比谷:778
西:726
国立:746
戸山:758
立川:727 *普通科(創造理数科の定員超過全員が受験の場合)
青山:761
八王子東:709
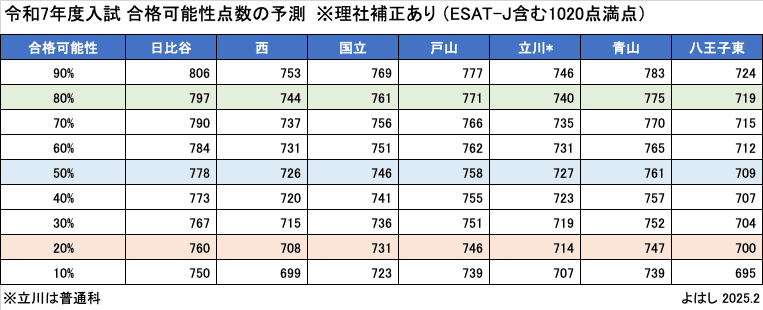
◆合格可能性80%の点数(3教科+理社変動補正)
日比谷:797
西:744
国立:761
戸山:771
立川:740 *普通科(創造理数科の定員超過全員が受験の場合)
青山:775
八王子東:719
1. 前提条件
まず、受検者の3教科の点数は正規分布していることが大前提です。そして、3教科(英数国)点数の標準偏差・理社の点数・内申点は高校ごとに違うが、同じ高校では年度に依存しない定数として設定しています。ただし、理社の点数は最後に調整する形に改良しています。
このような前提を置くと、進学指導重点校の合格最低点minTは、3教科平均点xと受検者倍率mの関数minT=f(x, m)となります。受検者倍率は当日に発表されるため、最終的には合格最低点minT=g(x)という一次関数になります。この推定モデルの詳細はこちらの記事をご覧下さい。
なお、立川高校は普通科が対象ですが、普通科受検者に創造理数科からのスライド受検者を加算して、受検者倍率は計算しています。その際、スライド受検者は創造理数科の不合格者全員と仮定しています。
2. 合格最低点予測表(令和7年度入試版)
まずは、合格最低点予測の基本となる「合格最低点予測表」を説明します。

この表は、過去6年(平成31年度入試〜令和6年度入試)と比べて、今年(令和7年度入試)の3教科平均点が、例年と同じ程度なのか、難化したのか易化したのかに応じて、合格最低点を予測する表です。
鍵となる今年の3教科の難易度(受験者平均点)については、過去6年の平均点の平均値(X)に対して、平均点の標準偏差(S)の幅で何パターンか計算しています。今年の3教科の難易度が過去と比較してどうかによって、合格最低点の予測値は変わります。
ただ、1校あたりのデータ数が6つしかないので、統計的な精度は高くないです。年数を増やせば、統計の信頼度は上がるのですが、長期になると定数の前提の「同じ高校では年度で変動しない」が崩れます。3年×2サイクルの6年がバランス良いところと判断して、過去6年との難易度比較にしています。
3. 合格最低点予測表の使い方
続いて、合格最低点予測表の使い方を説明します。この表を使って合格最低点を予測する際には、今年の3教科の難易度=3教科平均点を評価することが、最初に行うことになります。
今年の3教科は例年並みの難易度だと思ったら、「例年並み(X)」の行にある点数が合格最低点の予測値になります。難化したと思ったら、「難化(X-S)」の行にある点数が合格最低点の予測値です。逆に少し簡単になったと思ったら、「やや易化(X+0.5S)」の行にある点数が合格最低点の予測値です。
具体的な表の使い方を、日比谷高校を例に説明します。
基本的には、3教科の難易度が過去6年と比べてどうかで決まります。もし、今年の3教科の難易度が例年並みと判断した場合、表1の「日比谷」の列のグレーのゾーンで、「例年並み」の行にある179点が3教科平均点となります。これは過去6年間の平均点の平均値と同じです。

この3教科平均点での合格最低点の予測値は「日比谷」の列のブルーのゾーンで、「例年並み」の行にある778点となります。

そうではなく、今年はもっと簡単だったと判断したら、例えば「易化」の行を使って、3教科平均点は194点で合格者最低点の予測値を798点と予測できます。

逆に「かなり難化」と判断したら、例えば「かなり難化」の行を使って、3教科平均点は157点で合格最低点の予測値を748点と予測できます。

他の高校の合格最低点を知りたい場合には、知りたい高校の列を使って、3教科の難易度が例年と比べてどうかという感覚から、同じように該当する箇所を見ればいいです。
4. 理社の補正
これまでの合格最低点予測値は、理社の平均点が学校ごとには違うが年度によって変動しない定数として扱ってきました。大まかなレベルで、合格最低点を掴みたい場合は、ここまでの予測方法でよいと思います。
ただ、実際には理社の平均点は年度によって変動します。もう少し予測精度を高める場合には、定数としている理社の点数平均点の変動分を補正する必要があります。
過去15年の理社の平均点を集計すると、標準偏差σ=5.6となります。また四分位点は理社の平均点の中央値(114.5≒平均値)から-4点(110.4)と+5点(119.8)のところにあります。

ちなみに、昨年(令和6年度=2024年度入試)の理社は10年に1度くらいの易化で、第三四分位点を上回っていました。その結果、理科補正なしの合格最低点予測値は合否追跡データから見る値から大幅に外してしまいました。
これらを踏まえると、理社の定数は平均点の標準偏差である±5.6点≒総合得点で±8点くらいの変動は加味するようが良さそうです。この補正を加えると、合格最低点の予測値はこのように変わります。

例えば、日比谷で3教科はやや易化(X+0.5S)したけど、理社は難化したと感じたら、やや易化の行(796、788、780)のうち難化の列と交差する右端の数字の780が合格最低点の予測値となります。

5. 合格可能性点数①(3教科のみ)
ここまでは合格最低点の予測値を算出して、その説明を行ってきました。
でも、皆さんが本当に知りたいのは、自分が合格するのかどうかだと思います。この分析データを用いると、合格可能性が○%になる点数も統計的に算定できます。
具体的には、変数である3教科平均点の累積発生確率を用います。先ほどの合格最低点予測表の「変数(3教科平均点)」の行を抜粋して、その横に累積発生確率を記載したのがこちらです。

右端に追加した「累積発生確率」は、母集団が正規分布という前提から計算した値です。「難化」の欄の16%は、「平均点0点〜かなり難化〜難化」の発生確率を合計した数字になり、3教科平均点がこの数字以下になる確率が16%であることを意味します。同様に、「やや易化」の欄の69%は「平均点0点〜かなり難化〜難化〜やや難化〜例年並み〜やや易化」の発生確率を合計しており、3教科平均点がこの数字以下になる確率が69%であることを意味します。
変数である3教科平均点の累積発生確率がこのような数字になる場合、この段階では理社・内申点・ESAT-Jは定数のため、合格最低点予測値の累積発生確率も同じ値になります。

例えば、「日比谷」の列で合格最低点の「易化」の行は798点ですが、その「易化」の行を右に移動していき、「累積発生確率」の列を見ると84%とあります。これは合格最低点が798点よりも低くなる確率が、統計的には84%であることを意味します。逆に言えば、自己採点が798点を超えていれば、統計的には84%の可能性で合格するということです。
一方で、合格最低点が798点を超える確率は100%-84%=16%あります。これは、自己採点が798点の時、不合格になる可能性が16%あるということを意味します。
表9を見ると、日比谷高校の3教科平均点の「易化(X+S)」は194点で、累積発生確率は84%です。過去6年では、1回だけこの点数を超えたことがあります。R4年度入試の3教科平均点の200点です。6年に1回の発生は1÷6≒17%であり、194点を超える確率16%とほぼ一致します。
念のために、7校の過去6年分の42データを用いて、実際の入試での発生頻度を計算して、3教科平均点の累積発生確率を検証したのがこの表です。多少の乖離はありますが、実際の入試での発生頻度と統計的に算定した累積発生確率は近い数字にあることがわかります。

6. 合格可能性点数②(3教科+理社変動補正)
これまでは3教科平均点以外は定数として扱う場合の合格可能性でした。では、理社平均点が変動する場合は、合格可能性はどのようになるのでしょう。
理社平均点も変動する場合の合格可能性の計算は少し複雑です。3教科平均点の変動と理社平均点の変動は確率的に独立事象とみなした上で、正規分布の和の合成分布を計算する必要があります。
例えば、日比谷高校の場合、これまでの学力テスト(5教科)の得点分布は、3教科分布N(179.2, 14.5)と理社分布N(170, 0)の和の合成で、N(349.2, 14.5)の正規分布に従っていました。理社は定数扱いなので、標準偏差は0でした。
一方、理社の平均点も変動する場合には、3教科分布N(179.2, 14.5)と理社分布N(170, 5.6)の和の合成で、5教科点数の分布はN(349.2, 15.6)の正規分布に従います。5教科点数の標準偏差は、それぞれの標準偏差の単純合計でなく、分散の合成から計算しています。
同じように他の高校でも正規分布の合成を行って、合格可能性ごとの点数を計算するとこの表のようになります。3教科と理社の分布の合成によって標準偏差が大きくなるため、3教科単独よりも同じ点数の合格可能性が50%に寄っていきます(例:3教科単独だと798点で84% vs 理社補正ありだと797点で80%)。
6. 最後に
これまでの分析結果をグラフにすると、このようになります。中央の数字が合格可能性(=発生確率)50%の合格最低点予測値、帯は合格可能性20〜80%の幅となります。
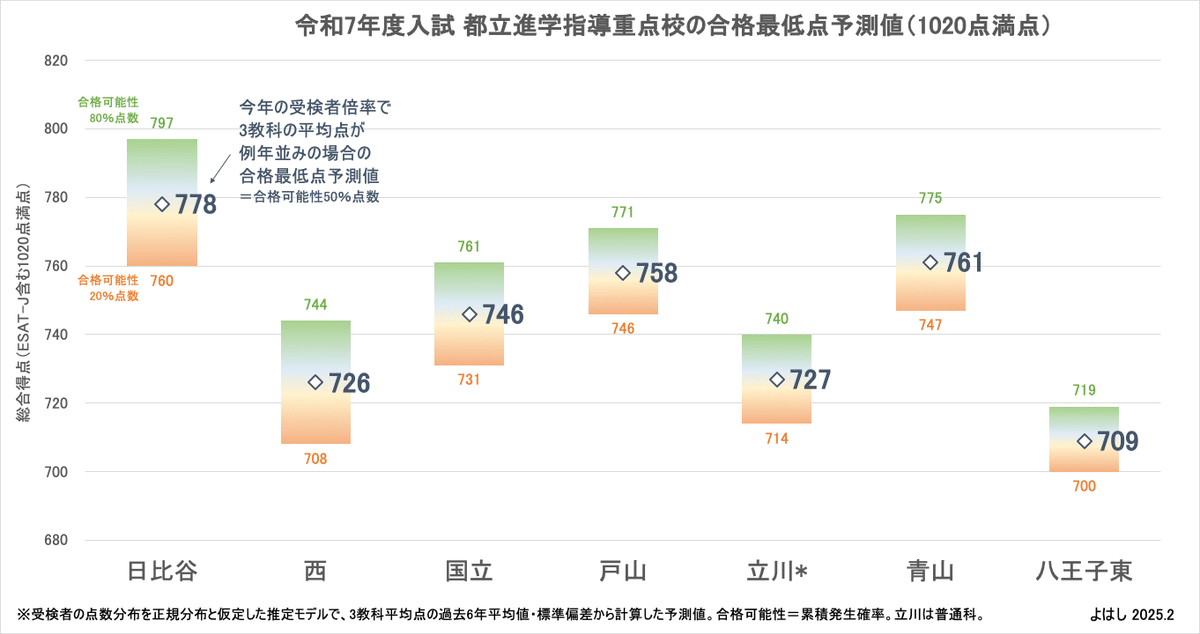
改めとなりますが、この記事の合格最低点の予測値は、一定の前提を置いた上で、過去の受検者平均点(3教科や理社)から統計的に予測した数字です。過去の予測値については、子供の塾の合否追跡データと照らし合わせると、学校や年度ごとに±5点くらいの誤差が確認されています。そのため、一つの参考数値くらいで眺めてもらえればと思います。
また、合格最低点の計算ロジックはある方が検証してくれていますが、今年の予測で入力した数字は私しか見ていないので、誤入力がある可能性もあります。また、合格可能性点数の理社補正は今年が初なので、第三者によるロジック検証は未実施です。もし、数値や計算に怪しいところがあれば、コメント欄でご指摘いただければ有り難いです。
