【R5年度入試】 都立•進学指導重点校の合格最低点（ボーダー）の統計予測モデル 〜日比谷・西・国立・戸山・立川・青山・八王子東〜

※この記事は2023年2月21日実施の令和5年度入試に関する予測です
※令和6年度入試版の合格最低点予測の記事も作成しました（2024年2月21日）
　→文末にリンクしておきました

実際の受検者平均点に関する記述を追記しました（2023/8/19）
立川高校の普通科について、創造理数科からのスライド受検があるとのご指摘をいただきました。当日発表の受検者倍率ではなく、実質受検者倍率で合格最低点の予測値を再計算しました。（2024/2/26）

子供が都立高校の一般入試を2月21日に受験しました。その高校に関する掲示板には、その日の夕方から、合格最低点を予想する投稿が次々と書き込まれていました。受験生はもちろん、保護者も気になっているのだろうと思います。

その高校も含む都立の進学指導重点校は、過去の受検者平均点は公表していますが、合格最低点（ボーダー）は公表していません。そのためか、高めの合格最低点の予想を書き込む人、自己採点の結果が不調で低めの点数を期待する人、過去の合格者の点数を引用する人、いろいろな書き込みがありました。

ただ、どの書き込みも今年度の合格最低点としての定量的な根拠はなく、個々人の直感と伝聞での書き込みがほとんどでした。合格最低点が公表されていないので、比較検討する数字がないのです。

そんな中、私は簡単な統計モデルを作って、子供の受験校の合格最低点を予測していました。そして、今週の3月1日に合格発表がありましたが、子供は予想通りの結果でした。

子供の高校受験は終わりましたが、おそらく来年度以降も、中学3年生とその親は受験校の合格最低点が気になるのでしょう。

そのため、来年度の受験生が気づいてくれるかわかりませんが、せっかく作ったので、久しぶりに「週末の趣味の統計分析」として、noteに投稿してみます。

今回の統計分析の基礎知識

使っている統計知識は、平均と標準偏差と正規分布だけです。ただ、中学生は習っていないと思うので、簡単に分析モデルの理屈を書いておきます。基本中の基本なので、統計学を勉強したことのある人は、読み飛ばしてください。

• ある年に300人がA高校の一般入試を受験して、3教科（300点満点）の得点が、このグラフのように分布していたとします。横軸が得点で、縦軸は1点あたりの人数です。

• 平均付近は1点あたりに5人、平均から離れると1点あたりの人数は減っていきます。緑の合計値（面積）が受検者合計の300名となります。計算すると、平均点は150.5点です。受験生のバラツキを示す標準偏差は25.0点となります。逆に言えば、この平均点と標準偏差の正規分布でグラフを作っています。

• さて、ある年のA高校の定員は200人とします。300人が受検するので、倍率は1.5倍です。この場合、得点の高い方（右側）から200人目のところが、合格最低点となります。計算すると141点となります。

• もし、A高校の定員が120人であったとすると、倍率は2.5倍です。この場合、得点の高い方から120人が合格となり、合格最低点は157点となります。

当たり前のことですが、同じ平均点で同じ分布でも、倍率によって合格最低点は変動します。このことを、もう少し統計的に表すとこのグラフになります。

緑のカーブは正規分布のグラフです。平均をX、標準偏差をσという変数で表現しています。横軸が変数でXとσの関数として表現されています。ここで横軸を得点とすると、縦軸はその得点の人数の受検者数に対する比率となります。よって、この緑色の面積全体が受検者数の合計です。

倍率2倍の場合、面積を半分に分ける中央線、すなわち平均値Xが合格最低点となります。倍率2.5倍の場合、正規分布から計算するとX+0.253σの線で右側の面積を合格者の比率の40％（1÷2.5）にできるので、合格最低点はX+0.253σ点となります。同様に、倍率1.5倍の場合は合格最低点はX-0.431σ点となります。

このように、受検者が正規分布に従うという仮定を置くと、合格最低点（B）は平均点（X）、バラツキ＝標準偏差（σ）、倍率（m）の関数となり、B＝f(X, σ, m）で表せます。

都立高校（進学指導重点校）の合格最低点のモデル化

関数の一つである平均点Xは総得点から算定されます。都立の進学指導重点校の一般入試の場合、総得点は更に3つ分解されます。英数国の点数（自校作成問題：x）、理社の点数（都立共通問題：y）、内申点（z）です。

この3つに一定の加重をかけた合計が総得点です。なお、内申点は9教科45点のうち、副教科を2倍する換算内申点（65点満点）です。当日点と内申点が7:3で1000点満点の場合、総得点＝1.4x + 1.4y + 4.6zとなります（係数は四捨五入してます）。
※2023年度からスピーキングの得点が加算されますが、過去との継続比較のために、スピーキングを除く総得点としています

総得点の平均点Xがこの3つの変数x, y, zによって決まるのであれば、合格最低点Bは5つの変数の関数となり、B＝g（x, y, z, σ, m）となります。5つも変数があると、合格最低点の予測は少し面倒になります。

そのため、今回は理社の点数（y）と内申点（z）の平均点は、学校によって異なるが年度によって変わらない定数として扱うことにしています。これにより、標準偏差σは総得点のバラツキでなく、3教科の得点のバラツキによって決まることとなります。

ここ5年ほどの進学指導重点校の相対ポジションは、それほど変わっていないので、受検する母集団は高校ごとに年度によって大きな変動はないと考えられます。そのため、3教科の標準偏差の年度変動も大きくないと考えられ、σも定数として扱うこととしています。

この前提の下、合格最低点BはB=h（x, m）と3教科平均点xと受検倍率mの2変数の関数の形にしています。定数として扱う3教科標準偏差（σ）、理社の点数（y）、内申点（z）は次のように設定しています。

• 3教科標準偏差：　駿台中学生テストの過去5年間（32回）の標準偏差の平均値37.0点を参考に設定

• 理社の点数：　インターネットで掲載されていた2018〜2022年度入試の受検者平均点を参考に5点単位で設定

• 内申点：　市進学院が公開している合格可能圏の内申点の男女平均値

それでは、それぞれの学校の合格最低点が何点と予測できるか、順番に見ていきましょう。まずは最難関校の日比谷高校です。

日比谷高校の合格最低点

まずは定数の設定です。3教科標準偏差は25点、理社の点数は170点、内申点は60としました。バラツキを示す標準偏差については、受検者は優秀層に絞られるので、駿台中学生テストのバラツキより小さいと考えられ、数値を2/3にしています。2/3の根拠は子供が通った塾からもらった追跡データなどをもとに決めています。

この定数のもとで、3教科平均点と倍率から導かれる合格最低点はこの表のようになります。表側（縦方向）が3教科受検者平均点、表頭（横方向）が受検者倍率です。表側の深緑の白文字の180点は、過去5年の3教科平均点の平均値です。

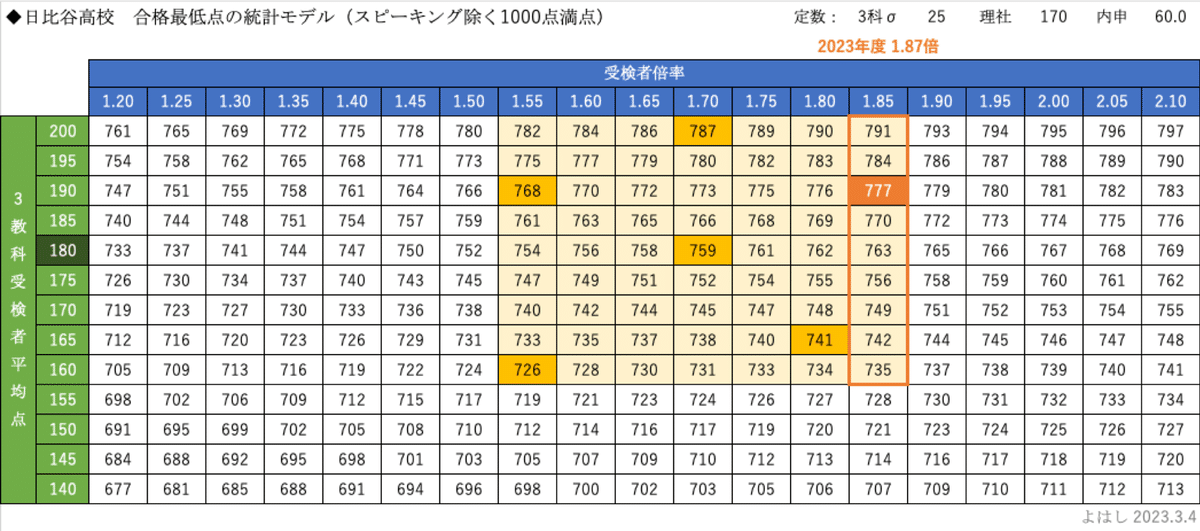
例えば、2020年度は3教科平均点が162.1点、倍率が1.55倍のため、表側160と表頭1.55が交差するオレンジの726点が合格最低点の予測となります（ESAT-J除く・明記ない場合は以下同じ）。他のオレンジの787点、768点、759点、741点も、過去の3教科平均点と受検者倍率の組み合わせから予測される合格最低点です。

さて、受検者倍率は入試当日に発表されます。2023年度は1.87倍でした。これを1.85倍と近似すると、右端のオレンジ色の枠が、過去5年の3教科平均点の上下幅から推定される合格最低点のレンジとなります。735〜791点で、かなり幅があります。

ここからどう絞るかは、かなり定性的な判断となります。インターネット掲示板などを見ると、今年の入試はそれほど難しくなく、過去の平均点の平均値180点よりは高そうな印象でした。

仮に3教科平均点を190点と見立てると、合格最低点は777点（オレンジに白文字）と予測できます。この数字に対して、ESAT-Jの平均を19点とした場合、1020点満点では796点台となります。

3教科平均点の見立てが違えば、合格最低点はブレますし、理社の難易度でも変わります。ただ、当日に受検倍率が1.87倍と決まった時点で、750点未満（ESAT-J含む770点未満）になる可能性は低いこともわかります。

＜追記＞
2023年度の3教科平均点は176点だったようです。易化という見立てが間違えており、難化してたようです。この場合、合格最低点の修正予測値は760点となります。ESAT-Jの平均を19点とすると、1020点満点での合格最低点は779点となります。

このように受検倍率と平均点の組み合わせで、合格最低点の予測を絞り込んでいます。それでは、他の高校も計算しているので、見ていきましょう。

西高校の合格最低点

定数は3教科標準偏差は日比谷よりも大きい30、理社平均点は165点、内申点は58.5点に設定してます。日比谷より倍率が低く、3教科平均点が低めなので、過去の合格最低点も低めに予測されています。特に、3教科平均点が低かった2021年度は700点未満でも合格できたようです（それだけ難問だった）。

2023年度入試は倍率が1.61倍で、合格最低点のレンジは684〜740点です。掲示板には国語の難化の書き込みが多く見られたので、平均点の平均値（165点）より今年の平均点は低い160点と見立てて、合格最低点は712点と予測しました。ESAT-Jを含めた1020点満点では730点前後となります。

ただ、合格発表後の書き込みを見ると、もう一つ下の705点くらいの可能性もありそうです（ESAT-Jを含めた1020点満点では720点台前半）。

＜追記＞
2023年度の3教科平均点は158点だったようです。ほぼ見立て通りの点数で、この場合、合格最低点の修正予測値は709点となります。ESAT-Jの平均を19点とすると、1020点満点での合格最低点は728点となります。

国立高校の合格最低点

定数は西高校とほぼ同じ。3教科平均点や倍率の分布もほぼ同じ。ただ、2023年度は受検倍率がかなり低い1.35倍なので、合格最低点レンジは686〜735点です。

あとは今年度の難易度をどう見立てるかですが、掲示板には易化したという投稿が散見されたので、3教科平均170点と見立てて、合格最低点は714点という予測です。ESAT-Jを含めた1020点満点では730点台前半となります。

＜追記＞
2023年度の3教科平均点は175点だったようです。見立ては少しズレました。この場合、合格最低点の修正予測値は721点となります。ESAT-Jの平均を19点とすると、1020点満点での合格最低点は740点となります。

戸山高校の合格最低点

定数は西・国立よりも、理社を5点下げて160点としました。人気がある高校のようで、受検者倍率は高めです。自校作成の3教科平均点も、西・国立より高いようです。ところが、2023年度は受検倍率が急落し、掲示板を見るとテストも難しかったようです。

そのため、受検倍率1.65倍のレンジ（714〜749点）の中で、過去平均より少し低めで、合格最低点は728点という予測です。ESAT-Jを含めた1020点満点では740点台半ばとなります。

＜追記＞
2023年度の3教科平均点は178点だったようです。この場合、合格最低点の修正予測値は732点となります。ESAT-Jの平均を18点とすると、1020点満点での合格最低点は750点となります。

青山高校の合格最低点

定数はさらに理社を5点下げています。内申点も少し下がります。日比谷よりも倍率が高いダントツの人気校だったのですが、2023年度は少し低め野倍率で1.79倍。この倍率での合格最低点のレンジは、703〜738点です。

あとは、今年度の難易度をどう見るかですが、掲示板は易化の書き込みが散見されたので、一番高めで738点を合格最低点という予測です。ESAT-Jを含めた1020点満点では750点台後半となります。

＜追記＞
2023年度の3教科平均点は191点だったようです。過去6年で一番易しかったようで、黄色のゾーンを上に突き抜けています。この場合、合格最低点の予測値は746点となります。ESAT-Jの平均を18点とすると、1020点満点での合格最低点は764点となります。

立川高校の合格最低点

ここは創造理数科が出来て、過去から一貫性ある比較が困難になりました。ただ、あくまで趣味の統計分析なので、割り切って計算しています。

内申はもう一段落ちて57.5で設定。倍率がかなり低めだけど、昨年より持ち直して、2023年度は1.33倍（事後記載 実質倍率は1.66倍）。掲示板を見ても、難易度の書き込みがほぼないので、3教科平均点は過去平均値（170）と見立てました。

この場合、合格最低点は702〜723点のレンジの真ん中あたりの716点という予測です。ESAT-Jを含めた1020点満点では730点前半となります。

＜追記修正＞
冒頭に記載した通り、202年度を実質倍率の1.67倍で再計算しました。予測のマトリクス表も修正しています。
実際の3教科平均点151点の場合、合格最低点の予測値（ESAT-J除く）は黄色の枠を突き抜けた690点となります。ESAT-Jの平均18点とすると、1020点満点では708点となります。
なお、別記事（過去6年分の合格最低点の推定）では、定数を一部変えているため、上記とは異なる合格最低点の推定値を掲載しております。

八王子東高校の合格最低点

最後です。理社も内申も更に下げて、それぞれ155点、57点で定数設定。ここは倍率が例年低い上に、2023年度は更に下げて1.22倍。ただ、3教科平均点がほぼ変動せず、過去5年は170〜180点の10点の幅に収まってます。そのため、合格最低点のレンジは677〜691点と、こちらも狭くなります。

2023年度入試は例年並みの難易度という書き込みが多かったので、平均値の3教科平均175点と見立てて、合格最低点は684点という予測です。ESAT-Jを含めた1020点満点では700点前後となります。

＜追記＞
2023年度の3教科平均点は186点だったようです。過去6年で一番易しかったようで、黄色のゾーンを上に突き抜けています。この場合、合格最低点の予測値は699点となります。ESAT-Jの平均を18点とすると、1020点満点での合格最低点は717点となります。

まとめ

このように統計分析から予測した2023年度入試の合格最低点を並べると、日比谷：777点（ESAT−J含む1020点満点では795点）、西：712点（730点）、国立：714点（732点）、戸山：728点（746点）、青山：738点（756点）、立川：700点（718点）、八王子東：684点（702点）となりました。

3教科の試験は自校作成で高校ごとに平均点も違うので、単純に合格最低点の高低と受検者の学力は連動しません。ただ、より上位の受検者を集める日比谷高校は、理社平均点も内申が高く、さらに倍率も高めなので、合格最低点が押し上げられて、800点に迫る点数になるようです。

また、トップ3といわれる日比谷・西・国立を除くと、人気＝受検倍率で合格最低点が分かれる傾向が見られます。23区にある戸山・青山は受検倍率が高いことで合格最低点が高まり、逆に多摩地区の立川・八王子は受検倍率が低いことで合格最低点も低めです。

2023年度は3教科平均点が根拠の弱い見立てなので、実際とは10点以上の差が出る可能性もあります。2023年度平均点が公表されたら、再度予測する予定です。

長々と書きましたが、あくまで統計モデルでの予測なので、一つの参考として眺めてもらえればと思います。

＜追記＞
実際の受検者平均点で検証しましたが、平均点の見立てが外れていることが多く、結果として予測値もズレていました。ただ、実際の平均点を用いた修正後の合格最低点については、子供の塾でもらった追跡調査データと照らし合わせると、それほど外していない印象です。

統計モデルはそれなりに良さそうなので、結局のところ、合格者最低点は3教科平均点をどう見立てるかに依存します。今回の分析でも、合格最低点の初期の予測値（掲示板書き込みからの推定）と修正後の予測値（3教科平均は公表値）の差は、±15点くらい出てしまいました。

±15点の合格最低点の予測のブレは、ボーダーギリギリの人にとっては影響が大きいので、この表から算出できる合格最低点の予測値（1000点満点）は、あくまで目安数字として捉えてもらえればと思います。

＜各年度の合格最低点予測の記事＞