受験科目数が総合偏差値に与える影響（駿台全国模試版）
駿台全国模試の判定基準を勘違いしていたことの訂正を行っていますが、どうせやるなら、ちょっと精度を高めたいと考えています。その対象の一つが科目数の違いの補正です。
過去の分析では、大学・学部・学科の判定偏差値が受験科目によって基準が異なることから、受験科目数の補正を行っていました。その際、受験科目数が総合偏差値に与える影響は、河合塾全統模試での分析結果（1科目増えると総合偏差値はマイナス1）をそのまま適用していました。
模試は違っても偏差値は相対値なので、科目数増減による総合偏差値増減の相対量は同等という前提で、そのまま適用していました。ただ、駿台全国模試の判定基準の勘違いの記事訂正の際に、科目数補正が必要になるので、せっかくなので、科目数補正の駿台全国模試版も計算してみます。
0. まとめ
ブログ等で確認できた成績表と駿台が公表している合格者平均偏差値から分析すると、駿台全国模試における科目数増減の影響は、1科目減につき総合偏差値＋1程度である。
この＋1は苦手科目が除外されて、得意科目だけで受験できることで総合偏差値が上昇する効果である（科目の構成差）。
この外には、科目数が減ることに伴って、1科目当たりの勉強時間が増やせることによる得意科目の成績上昇効果が存在するが、それを加味しても、1科目減につき総合偏差値への影響はせいぜい＋2程度ではないかと考えられる。
ただし、これは学力上位層のサンプル分析であり、学力中位層では、1科目減らした際の総合偏差値の上昇幅はもっと大きい可能性はある。
1. 公開されている成績表からの推定
駿台全国模試の成績表は個人がブログで公開しているものを、ネットで確認できます。そうした成績表から21件のサンプルを集めて、科目数が変わると総合偏差値（コース別偏差値）がどう変わるか分析してみました。サンプル数が21件というのは、google検索からの抽出効率が落ち始めたあたりで中止した結果です。
集めた21件の成績表の成績を一覧にするとこのようになります。
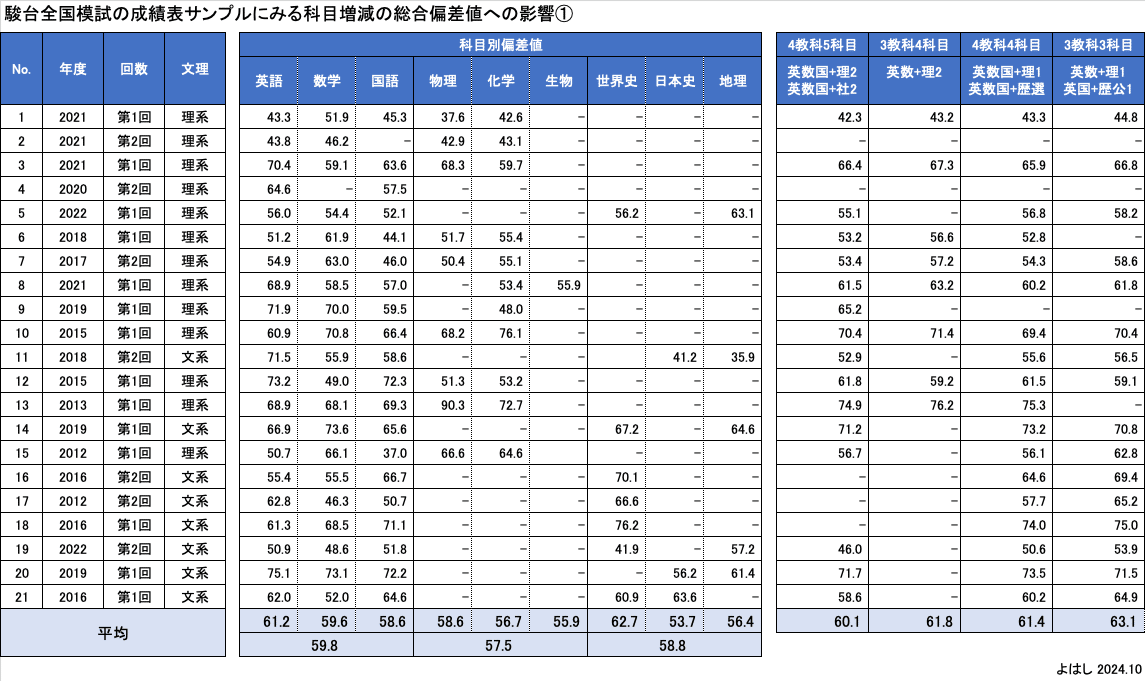
下段に21サンプルの平均を計算してあります。年度・回数も文理も違うので、本来なら同列で集計できないのですが、この記事では、過去10数年の駿台全国模試受験者を母数とした一つの標本として扱います。
順番に見ていきます。中央のブロックが科目別の偏差値です。個々の科目で見ると、平均値は凸凹しています。世界史の62.7が最大、生物（サンプル1）の55.9が最小です。科目ごとに個別に見ると、理社でサンプル数のブレの影響が大きくでるようです。
そこで、英数国、理科、社会の3グループで平均集計したのが、最下段です。鋭意数国59.8、理科57.5、社会58.8と概ね58前後に集まっており、科目数のブレはそれなりに平準化されている標本と言えそうです。
次に総合偏差値を集計したのが右側です。模試の成績表にあるコース別の偏差値を引用しています。サンプルによって受験科目が違うので、データの入り方が疎らですが、とりあえず平均を集計したのが下段になります。
4教科5科目（英数国理2または英数国社2）の東大型では平均60.1、これが3教科3科目（英数理または英数社）になると63.1に＋3となります。ただし、この2科目減での+3には、個々のサンプルで受験科目が減ることで総合偏差値が上昇した要素と、サンプル間のコース別偏差値の有無の違い＝構成差の要素があり、単純に2科目減ると3増えるとは言えません。
そこで、個々のサンプルごとに科目数変化の総合偏差値を先に集計して、それの平均を見てみることにします。集計したのがこの表です。
グリーンのブロックの左が、4教科5科目（4-5）から3教科4科目（3−4）に減った時の総合偏差値影響です。これは理系で英数国理2（東大・京大型）から、英数理2（国公立一般や早慶の理系）のように、国語がなくなるケースです。そのため、理系のサンプルにしか科目数減少の影響数字は出ません。この国語減少の影響を見ると、1つのサンプルを除いてプラスになっており、増減全て平均にすると、4教科5科目からの国語の減少で+1.3となりました。
同様にグリーンの中央が4教科5科目（4-5）から4教科4科目（4−4）に減るケースです。これは英数国社2（東大文系）から英数国社（一橋文系）が代表例で、理社2科目から理社1科目になるケースです。これはプラス影響とマイナス影響が半々くらいに分布し、全体では4教科5科目からの理社1科目減で＋0.8となりました。
最後にグリーンの右が4教科4科目（4−4）から3教科3科目（3−3）に減るケースです。これは英数国理から英国理、英数国社から英国社のようになるパターンで、主に国立受験と私立受験の違いと見なせます。この場合、4教科4科目から数学または国語の1科目減で＋2.1と最も大きい影響数字となりました。
これらを平均すると、21件のサンプルでの分析結果としては、駿台全国模試では1科目減による総合偏差値の影響は＋0.7〜2.1で、平均+1.4となりました。この増分は苦手科目が外れることで、得意科目だけで受験できることで、総合偏差値が上昇する分と言えます。
2. 合格者平均偏差値からの分析
上記の分析結果（1科目減につき総合偏差値＋1.4）は、あくまでサンプルからの算定値です。これだけだと心許ないので、別の方法でも算定してみます。その算定方法には、駿台が公表している難関国立大の合格者平均偏差値を用います。
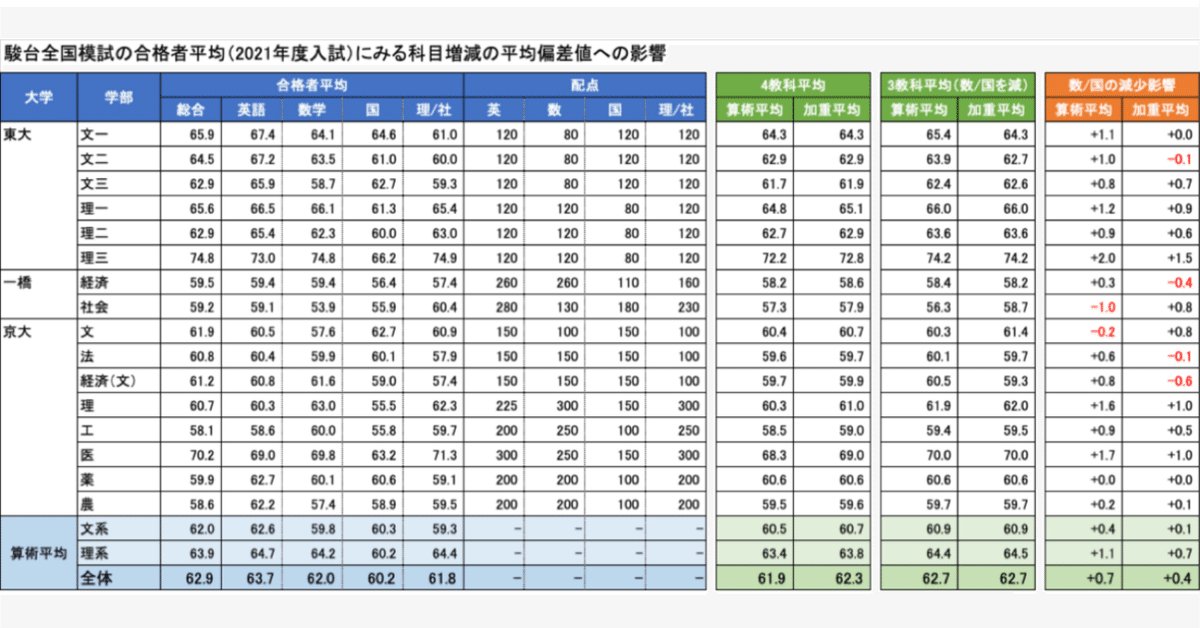
こちらのホームページから、4教科5科目または4教科4科目の受験が必要な東大、一橋大、京大の合格者平均偏差値を抽出したのが、こちらの表です。
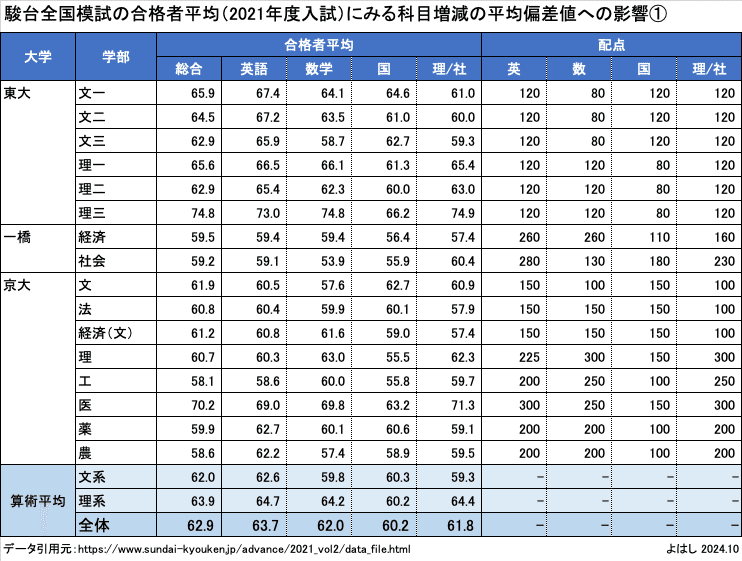
左側がホームページに掲載されていた合格者平均偏差値です。総合以外に科目別の数字も入れています。また、右側が入試の配点です。2021年度ではなく2024年度入試の数字を入れているため、多少の違いがある可能性はあります。
合格者平均の下段の算術平均を見ると、文系では数学と社会が、理系では国語が相対的に低い値になっていることがわかります。一般に言われるように、文系は数学が苦手、理系は国語が苦手というのが数字に出ているようです。こうした苦手科目が総合偏差値をどの程度押し下げているかを分析してみます。
ただし、駿台の総合偏差値は合計点に対する偏差値であり、科目を減らす場合、平均点と標準偏差の再計算が必要ですが、ネットで手に入る情報からは再計算ができません。そのため、全統模試のように各科目の偏差値の平均を使って、全体への影響度を推定していきます。
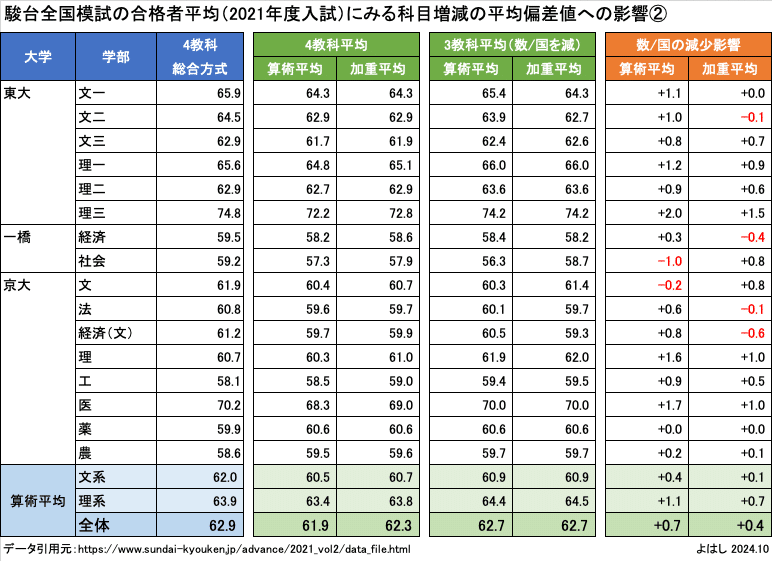
まずは4教科平均です。算術平均は表3の英数国＋理社を単純に平均した数字、加重平均は配点で重み付けして平均した数字です。全体平均を見ると、総合方式62.9に対して、算術平均は61.9、加重平均は62.3となっています。
入試科目の配点は、文系では苦手科目の数学が低く、理系では苦手科目の国語が低くなっています。単純平均にすると、苦手科目も得意科目も同列なので、加重平均より算術平均の方が平均値は低くなります。一方、もともとの総合方式は配点で加重しているため、加重平均の方が総合方式に近い数字になっています
総合方式と平均方式では、加重平均を使えば、4教科ではそれほど差が出ないことが確認できました。続けて科目数を減らした平均も見てみます。
3教科平均の列を見ると、平均値は算術平均も加重平均も一致しています。これは文系の数学や理系の国語の配点がもともと低いのに対して、それを除外した3教科ではの配点差が小さいことに起因しています。
3教科平均と4教科平均の差を計算すると、右端の列のように、算術平均では＋0.7、加重平均では+0.4となります。総合方式にする場合は、もう少し拡大すると考えられますが、東大・一橋大・京大の合格者平均偏差値においては、科目数を減らしても1科目あたり＋0.4〜0.7にしか総合偏差値は上昇しないようです。
3. 考察
受験科目を減らす場合の総合偏差値への影響は、サンプル分析からは平均＋1.4、東大・一橋大・京大の合格者平均偏差値の分析からは＋0.4〜0.7となりました。後者が数値が小さいのは、学力優秀者はどの科目も一定以上の成績となるため、科目数を減らしても、総合偏差値に影響が出にくいのだろうと考えられます。そう考えると、他の大学の合格者平均偏差値から分析すると、上昇幅はもう少し大きくなりそうです。
ただ、私の分析記事では地帝・早慶以上を扱うことが多いので、これまでの分析からから、単純に受験科目を1科目減らすと総合偏差値は＋1程度上昇する、と考えてよいと判断します。
なお、この上昇幅の外に、科目数を減らすことにより、1科目あたりの勉強時間を増やせることで、得意科目の成績が上昇する効果が存在します。ただ、実際には成績優秀者ほど受験科目数が多い大学を受験するため、実際に科目数を減らしても、総合偏差値が大きく上昇するとは考えにくいです。
例えば、東大文系の英数国社2と、一橋大・京大の文系の英国社1では、総合偏差値の平均値を計算すると、東大文系64.4に対して、一橋大・京大文系で62.0で、差は2.4です。
ここで、個別の科目の差を計算すると、英語6.9、数学3.6、国語3.9、社会1.3で平均3.9です。3.9と2.4の差が1.5で、このうち1が社会1科目分の影響とすると、それ以外の影響はせいぜい0.5となります。
そのため、1科目あたりの勉強時間を加味しても、1科目減の総合偏差値影響は2を超えることはないと考えられます。
4. 最後に
駿台全国模試の科目数減が総合偏差値に与える影響は＋1（0.4〜1.4）程度で、全統記述模試の＋1（正しくは+0.9）とほぼ同等でした。
ただ、よくよくサンプルを見ると、成績表サンプルの平均偏差値は60弱、合格者平均の方も東大・京大・一橋なので、学力上位層に偏ってます。学力中位層だと得意科目と苦手科目の差が大きくなるはずなので、1科目減らす場合の総合偏差値上昇はもっと大きいかもしれません。
いずれにせよ、東京一工・地帝・早慶のレンジを対象に分析するのであれば、これまでの科目補正はそれほど間違ってなかったようです。そのため、今後の記事訂正・分析でも、科目補正は1科目減につき＋1で計算することにします。