模試の判定偏差値と合格者平均偏差値の関係 ①駿台全国模試（大学受験）

よはし

2024年10月19日 21:56

先日にお詫び記事を書いた通り、これまでの記事で駿台全国模試の判定偏差値の基準を勘違いしていました。一方、その勘違いがあろうがなかろうが、模試の判定偏差値と合格者平均偏差値の関係は、模試ごとに違いがあるようです。

そこで、今回は改めて駿台全国模試の判定基準や分布の特性を確認した上で、合格者平均偏差値との関係を見て行きます。合わせて、駿台模試の判定偏差値を用いた各種推定のためのモデル（駿台模試判定モデル）を再構築します。

なお、明言ない場合は、駿台全国模試は高3のものを対象としています。

0 まとめ

サンプルの分析の結果、駿台全国模試の判定基準には、次の特性があることがわかった。

判定幅は、平均すると、A-B差が3、B-C差とC-D差が4となっている。
受験者の分布は、平均すると、A判定を1とした相対値で、A： B：C：D：E＝1.0：0.7：2.1：2.2：2.5となっている。ただし、実際の倍率と照らし合わせると、E判定はもっと大きな数字になると考えられる。
文系偏差値＝理系偏差値＋2〜3となる。
科目を1つ減らすと、総合偏差値は＋1となる。
難関進学校生徒の参入と浪人の受験で、高1・2の偏差値ー3＝高3の偏差値となる。
倍率3倍程度の一般的な国公立・私立大では、合格者平均偏差値＝A判定偏差値−4となる。
ただし、受験者構成と判定定義の関係から、合格者平均とA判定の差は倍率が増えると拡大し、倍率が5〜7倍の学部・学科では、合格者平均偏差値＝A判定偏差値−5〜6となる。

1. 駿台全国模試の判定の基準の特性

①判定間の幅

駿台全国模試の判定はA判定（合格可能性80%）、B判定（60%）、C判定（40%）、D判定（20%）となっていますが、判定間の幅は大学・学部・学科によって異なり、更に開催回によっても異なるようです。

判定幅は駿台模試判定モデルを作る上で、重要な指標です。そこで、ブログで公開されている成績表と個別に情報提供していただいた方からのデータを集計して、判定幅を計算してみました。集まった173サンプルを集計したのがこの表です。

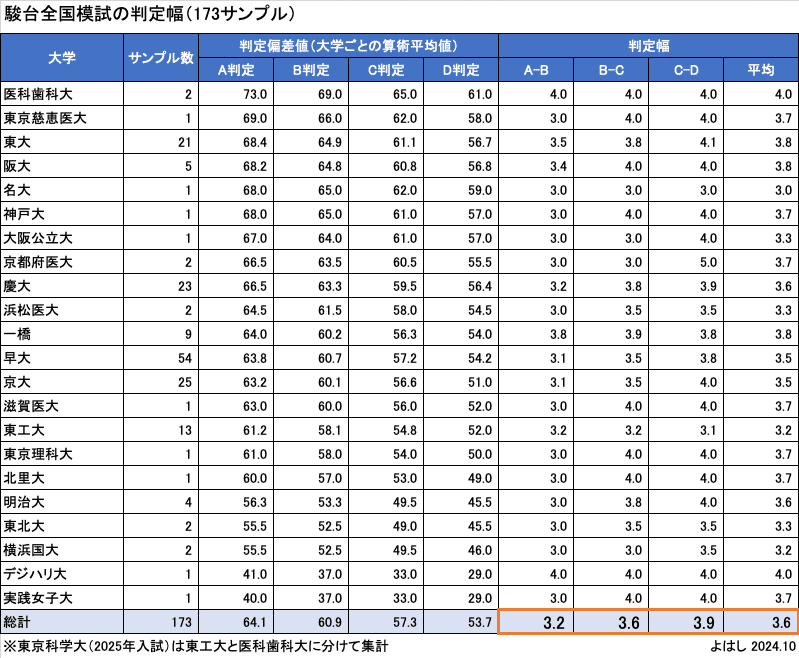
多少の凸凹はありますが、A-B差は約3、B-C差とC-D差は約4となりました。この時、大学ごとのA判定平均と判定幅の平均値の間には、相関はほぼないようです（R^2=0.18）。また、文系と理系、医学部とそれ以外の平均値の差もほぼゼロでした。

そのため、駿台模試判定モデルの判定幅は、全ての大学に一律でA-B差は3、B-C差とC-D差で設定することにします。

②判定ごとの定員構成比／分布比率

次に判定ごとの受験者の分布を検討します。これはモデルを作る際に、判定ごとの人数（定員構成比）を設定する時に使います。

こちらもサンプルを集めてみました。ただ、サンプル数は21件と少ないので精度は低いですが、一旦集計しています。

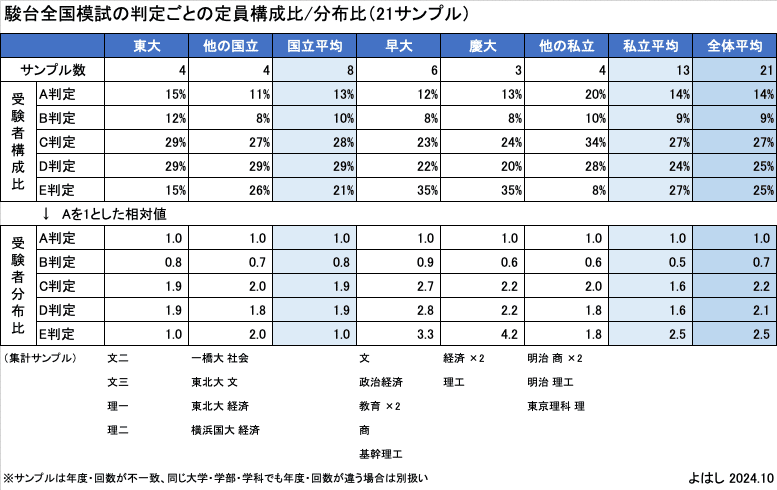
上段が集計した受験者数の定員に対する構成比、下段がA判定人数を1とした時の各判定の相対値です。いくつかグループ分けしています。

受験者構成比を見ると、A判定の受験者は全体の1〜2割程度であり、大半の受験者がC判定以下であることがわかります。また、受験者分布比を見ると、B判定はA判定より少なく、C判定とD判定はそれぞれA判定の2倍程度が存在することがわかります。

ただし、この受験者構成では実際の倍率と合格者を一致させることができません。志望校判定は8校までなので、特に私立の併願先でギャップが出るのだろうと思います。おそらく、倍率が高いところは、チャレンジ受験のE判定が膨らむはずです。この点については、モデルを作る際には少し補正をかけます。

③合格目標ラインと合格者平均の差

駿台は2021年度入試において、難関国立10大学の主要学部の現役合格者平均偏差値を公表しています。
https://www.sundai-kyouken.jp/advance/2021_vol2/data_file.html

その現役合格者平均偏差値を、駿台が設定している合格目標ラインと比較したのがこの表です。合格目標ラインは国立私立や科目の補正を行ったA判定相当の偏差値という定義となっています。なお、以下では受験者平均でなく合格者平均のため、現役と浪人はほぼ同等で扱えると考えられるので、現役合格者平均＝（現浪合計の）合格者平均として扱います。

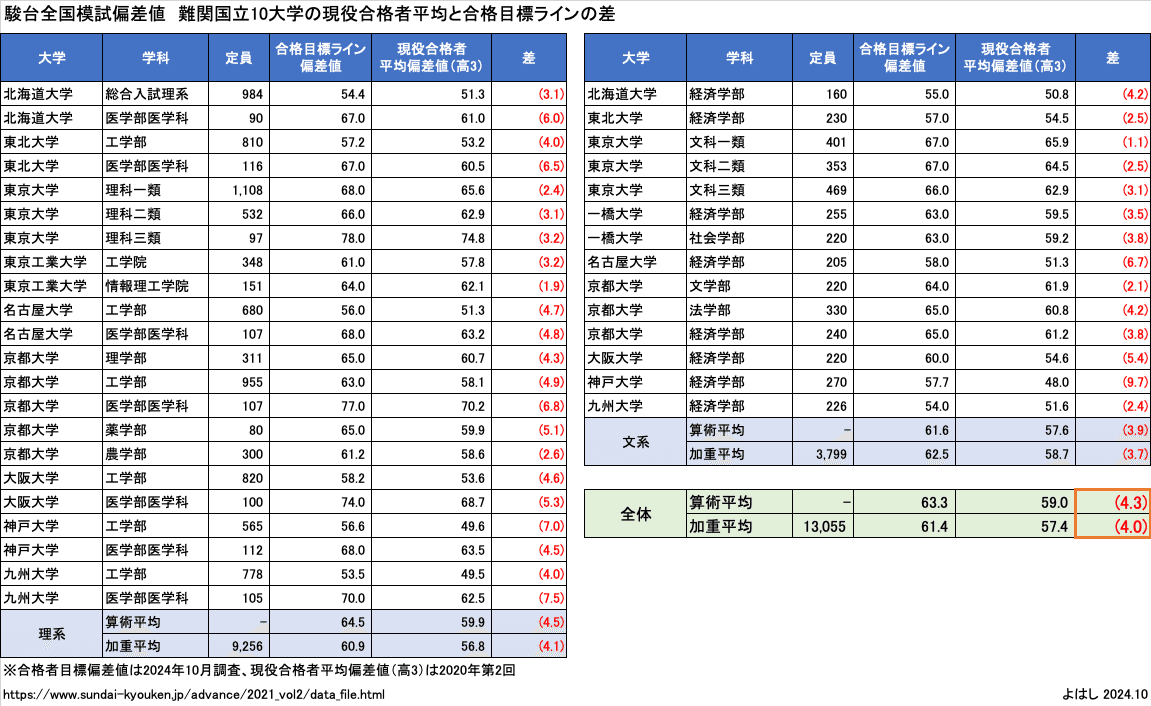
この表を見ると、算術平均でも加重平均でも、文系でも理系でも、合格者平均偏差値は合格目標ライン偏差値（A判定80％相当）マイナス4程度にあることがわかります。後ほど、倍率による影響を検証しますが、一旦、駿台全国模試では「合格者平均＝A判定ー4」を採用することにします。この場合、②の設定により、「合格者平均＝ B判定ー1」で、合格者平均偏差値はB判定とC判定の間に位置します。

④文系と理系の差

同じ現役合格者平均偏差値を用いて、今度は文系と理系の差を見てみます。

駿台が公表している現役合格者平均偏差値は、高3だけでなく、高1・2時点の数字もあります。高1・2は英数国で文理で共通の母集団、高3は受験科目による文理別の母集団となります。であれば、高1・2と高3の差を分析すれば、文系偏差値と理系偏差値の差を算定できます。それを計算すると、この表のようになります。

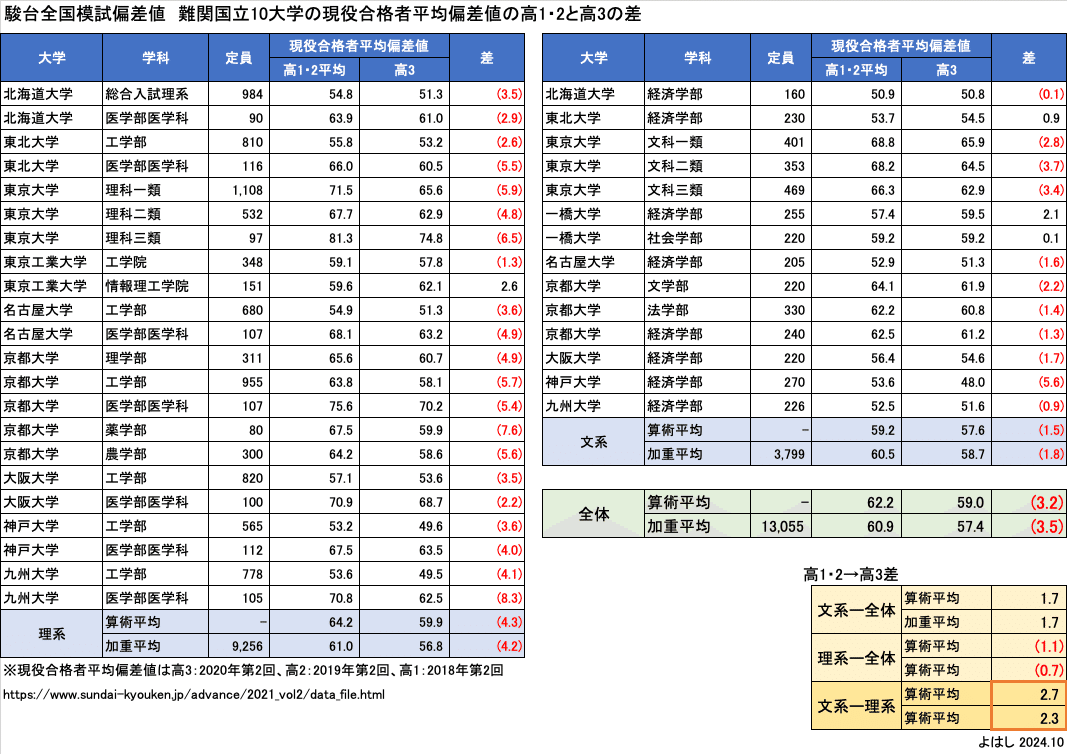
高校1・2平均と高3の差を見ると、ほとんどが下がっています。平均すると、文系ではマイナス2程度、理系ではマイナス4程度で、全体平均でマイナス3程度です。全体平均のマイナス3は浪人が入ることと、難関校の受験者が増える影響と考えらます。

この全体の母集団影響のー3.2〜3.5を除外すると、右下のオレンジ部分のように、高1・2から高3で合格者平均偏差値が、文系は＋1.7、理系はー0.7〜1.1となります。これが文系と理系に母集団が分かれたことによる偏差値への影響と考えられ、「文系偏差値＝理系偏差値」＋2〜3と言えます。

なお、モデルを作る際には計算を簡単に行うために、文系＝理系＋2 ⇔ 文系＝全体−1 ⇔ 理系＝全体+1で補正を行うことにします。

⑤科目増減の総合偏差値への影響

これは前回の分析の通り、科目数を1減らすと、総合偏差値は＋1です。苦手科目が除外され、得意科目が残ることで、科目数を減らすほど総合偏差値は上がるようです。

⑥高1・2と高3の差

上記は高3の駿台全国模試が前提です。もし高1・2の偏差値と比較する場合は、④の途中で計算した通り、高3になると平均で偏差値がー3.2〜3.5になります。そのため、高1・2の駿台全国模試偏差値ー3＝高3の駿台全国模試偏差値で概算できると考えられます。

2. 駿台模試判定モデルの構築

これまでの分析で、駿台全国模試の判定基準の特徴がわかってきました。ただ、個々の大学・学部・学科ではブレがあるので、今後の分析をシンプルに行っていくためには、一般的なモデル化が必要です。そこで、それぞれで算定した平均傾向からモデルを作ります。

上記の分析で算定した数値を参考に、モデル構築時に採用する値は以下とします。

合格可能性
A判定：80％、B判定：60％、C判定：40％、D判定：20％、E判定：5％
※過去の記事の分析で、偏差値+10以上の上振れ可能性は5％程度あることから、E判定→B〜C判定≒合格最下位ラインの可能性として、E判定＝5％とした
判定幅
A以上：3、A-B：3、B-C：4、C-D：4、D-E：4
※A以上とD以下は理論上は無限ですが、受験者は輪切り構造になるという前提で一つ横の判定と同じ幅で設定
判定幅の平均偏差値
A判定平均＝（（判定偏差値＋2）＋（判定偏差値＋1）＋判定偏差値）÷3＝判定偏差値＋1
同様の計算により、B判定の平均＝判定偏差値＋1.0、C〜D判定の平均＝判定偏差値＋1.5
E判定は下限がないため、D判定基準偏差値-2.5
A：B：C：Dの受験者構成比
東大 1.0：0.8：1.9：1.9、国立一般 1.0：0.7：2.0：1.8、早稲田 1.0：0.9：2.7：2.8、慶應 1.0：0.6：2.2：2.2、私立一般 1.0：0.6：2.0：1.8
E判定の受験者構成比
倍率ー（A+B+C+Dの構成比の合計）
※受験者構成比の合計が100％になるようにE判定で調整
A判定の構成比
倍率をm、受験者構成比のA:B:C:Dを1：b：c：dと変数設定すると、
A判定の構成比＝（100％-0.1m）÷（0.75＋0.55b＋0.35c＋0.15d）
※合格者構成比の合計が100％となるように逆算

この設定で、例えば、倍率2.8倍（国公立大平均）の定員100人（＝100％）でA判定偏差値60の国立大学・一般学部で作ると、このようになります。E判定は計算の都合から判定幅4で下限設定しています。

この模試判定モデルに対して、A判定偏差値は60で固定して、倍率を変えたのが次の表です。なお、倍率は7倍を上限として設定しています。

右の列を見るとわかりますが、一般的な国公立大の倍率の3倍程度なら、合格者平均＝A判定ー3.3〜3.9です。先ほど、難関国立10大学の実際の合格者平均から算定したのが、合格者平均＝A判定−4でしたので、ほぼ近い結果となっています。

また、右の列を下に見ていくと、倍率が高くなるにつれて合格者平均とA判定の差が拡大し、倍率5〜7倍では合格者平均＝A判定−5〜6になるようです。

今度は、倍率を固定してA判定偏差値を変えたらどうなるか見てみます。倍率は国公立大平均の2.8倍としています。

以前のモデルと異なり、判定幅は一定にしているので、リニアに右上に伸びる形になっています。最下段に合格者平均偏差値を計算していますが、判定分布と倍率が固定のため、全てA判定偏差値-3.6となっています。

3. 駿台模試判定モデルの利用例

このように構築した駿台模試判定モデルは、「○○大の進学者は△△大に何人合格するのか？」という記事で利用しています。具体的には次のような表を用いて計算します。

左はA判定偏差値60の国立大学・一般学部（X大学）の入学者の偏差値分布です。具体的には、表5の合格者の構成を、A判定偏差値65の受験者構成に合わせて集計しています。

このようなX大学の入学者（＝合格者）が、A判定偏差値65の国立大学・一般学部（Y大学）を受験した場合の合否をシミュレーションしているのが右側です。例えば、X大学の入学者には偏差値62〜64の学生が11人います。この11人がY大学を受験する時はB判定（60％）のため、合格者は11人×60％＝7人という計算となります。

この表を計算すると、もしもX大学の入学者100人がY大学を受験する場合に合格できるのは27人であることがわかります。

4. 最後に

今回は駿台全国模試の判定基準を改めて分析して、駿台模試判定モデルを再構築しました。今後、このモデルを用いて、過去記事の修正と新たな分析を行う予定です。