
東京一工・地帝・早慶の都道府県別進学者数の重力モデル
ここ数ヵ月間、趣味で受験データの統計分析を行なっているのですが、地理的な配置(距離)が難関大学の進学傾向に影響を与えている現象がいくつか見られています。
大学ランクに基づく定員数は、東日本と西日本でそれぞれで底数3〜4の指数となる(大学ランクの中心地理論)
早稲田大・慶應大の現役本命率は、高校の入試偏差値に正の相関をして、大学と高校の距離に負の相関をする(早慶現役本命率の重回帰分析)
実家を離れて遠方の大学に進学するというのには、一定のハードルがあるのですが、その場合でも距離が何らかの影響を及ぼしているようです。そこで、今回は大学の地理的配置(距離)が入試に与える影響を、重力モデルを用いて分析してみます。
0. まとめ
東京一工・地帝・早慶の進学者数には、重力モデルが当てはまり(重回帰の補正R2=0.7032)、大学の定員と都道府県の高3生徒数に比例し、出身都道府県の距離に反比例する。言い換えれば、大学の定員が多く、都道府県の高3生徒数が多く、距離が近いと、その都道府県から大学への進学者数は増える。
この重力モデルに大学の入試偏差値を変数として追加すると、同様に重回帰モデルが当てはまり(重回帰の補正R2=0.7068)、大学の進学者はその大学の入試偏差値に反比例する。このことは、ある都道府県から同じ距離にある大学への進学者は、大学の難易度が上がるほど減ることを意味する。ただし、このメカニズムは解明できていない。
1. 重力モデルとは
ニュートンの万有引力の法則は、天体の間の引力がそれぞれの天体の質量に比例し、距離に反比例することを示す法則(方程式)でした。これを社会科学に適用し、二つの対象の間のある説明変数が、対象それぞれの変数に比例し、対象間の距離に反比例する場合の説明モデルが、重力モデル(gravity model / gravity equation) です。
私は国際経済学で、二国間の貿易量を説明するモデルとして学習しました。具体的には、「二国間の貿易額は、両国のGDP(質量)に比例し、国の距離に反比例する」というものです。略式の方程式にすると、Trade = 定数A × GDP1 x GDP2 ÷ 距離Dとなります。
重力方程式は距離の2乗ではないのかという突っ込みがあるかもしれませんが、計算するときに両辺の自然対数(ln)を取って、足し算に変える際に係数がつくので、距離は2乗になるとは限らず、何らかの乗数となります。自然対数を取った方程式は、εを誤差項として、ln(Trade)=A + α × ln(GDP1) + β × ln(GDP2) + γ × ln(D) +εです。γは通常はマイナスの係数となります。
今から20年以上前には、この貿易の重力モデルは、さらに変数を加えて精度を上げる研究が行われていました。英語圏のフラグを付けるとか経済連携協定のフラグを付けるとかです。
また、重力モデルの適用は貿易額だけでなく、人の移動や国際電話の発着回数などにも当てはまるようで、社会科学の色々な分野で取り上げられているようです。今回はこの重力モデルを大学受験に当てはめてみます。
2. 大学進学者数の重力モデル構築
今回、重力モデルで分析するのは、大学受験における東京一工・地帝・早慶の都道府県別進学者数です。東京一工=東京大・京都大・一橋大・東京工業大、地帝=北海道大・東北大・名古屋大・大阪大・九州大、早慶=早稲田大・慶應大です。全部で11大学となります。
具体的には以下のような被説明変数と説明変数となり、データ数は11大学×47都道府県で517件です。
①被説明変数
上記の大学の都道府県別の進学者数が被説明変数です。入手できる最新年度の数字となります。早慶は合格者数しか都道府県別に開示しないため、本命率=進学者数÷(合格者数+補欠合格者数)で算定した本命率を、大学ごとに都道府県別合格者数に乗算して算定しています。
各大学が公表している数字を採用しており、どの大学も出身高校の所在地を基準にしています。なお、都道府県単位で公表していない場合は、高校別合格者数を集計しているブログなどから数字を入手しています。また、進学者数が0人の場合は、自然対数が計算できなくなるため、全てのデータに+1名の調整を行っています。
②説明変数
大学定員
万有引力の法則において、物質の質量に当たる変数です。定員が多い大学ほど、対象の都道府県からの進学者数が増えるはずなので、正の相関があると思われる変数として採用しています。具体的には、大学定員=一般入試定員≒都道府県別進学者数の合計値で計算しています。都道府県の高3生徒数
万有引力の法則において、もう一つの物資の質量に当たる変数です。都道府県の高3生徒数が多いほど、受験者が増えて、対象大学への進学者が増えるという仮説のもので、同じく正の相関がありそうな変数として採用しています。都道府県庁の距離
万有引力の法則において、反比例変数の距離に当たる変数です。対象大学がある都道府県庁と出身者の都道府県庁の直線距離を採用しています。なお、対象大学と出身者の都道府県が同じ場合、距離が0となり、自然対数が計算できなくなります。そのため、都道府県庁から自宅までの都道府県内移動があるという前提で、距離には一律で20kmをプラスしています。対象大学の入試偏差値
入試偏差値が進学者数に影響するかを分析するために、追加する変数です。例えば、東京にある東大・一橋大・東工大・早稲田大・慶應大に対して、同じ都道府県から進学する場合、5つの大学の進学者数の差が出るはずです。この差のうち変数1(大学定員)では説明しきれない要素=残差を説明する仮説として採用しています。
具体的には、駿台全国模試の合格目標ライン偏差値(A判定80%相当)を用いてます。少し古いですが、2023年7月に集めたデータです。各大学について、経済学系の学部と工学系の学部の駿台偏差値の単純な加算平均を算定しています。都道府県の代表国立大の入試偏差値
こちらも偏差値の影響を評価するための追加変数です。出身都道府県にある最も難易度の高い国立の総合大学の入試偏差値です。定義は上記4と同じです。基本的には各都道府県に代表的な国立大学があるのですが、奈良県だけは共学の国立の総合大学がないため、奈良女子大となります。
③分析データのサンプル
このような被説明変数と説明変数で構成される分析データは、サンプルを見ると、このようなデータセットとなります。

④変数間の多重共線性のチェック
多重共線性のチェックでVIFを計算しましたが、全て3以下でした。ただ、都道府県の高3生徒数がVIF:2.64、都道府県の代表大学の入試偏差値がVIF:2.63とやや高めのようです。分析結果を見る際には、少し注意が必要ではあります。
3. 重力モデルの検証
それでは、対象大学の都道府県別の進学者数に対して重力モデルが当てはまるかを順番に見ていきます。
①基本セット
まずはシンプルな基本セットです。重力モデルの方程式にすると、こうなります。
ln(進学者数)= A + α × ln(大学定員)+ β × ln(都道府県の高3生徒数)+ γ × ln(都道府県庁距離)+ ε
※A:定数、α/β/γ=係数(定数)、ε:誤差項
この重力モデルの方程式に分析対象データ517件を投入して、重回帰分析を行うと、このような結果となりました。

補正R2は0.7032と高い相関を示しており、有意Fも極めて小さく、この変数の組み合わせは問題はないようです。変数は3つともP-値が1%未満で、それぞれが進学者数に影響していると言えそうです。都道府県間距離はきちんとマイナスの係数=距離に反比例になっています。
この結果を見ると、対象大学の都道府県別進学者数に重力モデルは当てはまると考えられます。
②対象大学の入試偏差値を追加したモデル
続いて、対象大学(東京一工・地帝・早慶)の入試偏差値を変数に追加して、入試難易度が進学者数にどのような影響を与えるか見てみます。今回の重力モデルの方程式と重回帰分析の結果はこうなります。
ln(進学者数)= A + α × ln(大学定員)+ β × ln(都道府県の高3生徒数)+ γ × ln(都道府県庁距離)+ δ × ln(対象大学の入試偏差値)+ ε
※A:定数、α/β/γ/δ=係数(定数)、ε:誤差項

決定係数は基本モデルより少し上昇して、補正R2=0.7068です。有意Fも問題なく、基本モデルの3つの変数もP-値は1%未満です。新たに追加した大学の入試偏差値は、他の変数よりはP値が高いですが、それでも1%未満の0.68%(0.0068)で、この変数も進学者数に影響を与えていると言えそうです。
大学入試偏差値の係数はマイナスなので、他の変数が同じなら、難易度が高い大学ほど進学者数が減るとういことになります。例えば、同じ都道府県から同じ距離の大学である東大・一橋大・東工大・早稲田大・慶應大への進学数は、大学定員が同じなら、入試偏差値が高いほど進学者数が少ないということになります。実際には大学定員が違うので、その影響もあるなど、少し複雑です。
③都道府県の代表大学の入試偏差値を追加
最後にもう1つ変数を追加します。地元を代表する国立総合大学のレベルが、東京一工・地帝・早慶への進学者に影響を与えるか見てみます。重力モデルの方程式と重回帰分析の結果はこうなります。
ln(進学者数)= A + α × ln(大学定員)+ β × ln(都道府県の高3生徒数)+ γ × ln(都道府県庁距離)+ δ × ln(対象大学の入試偏差値)+ ζ× ln(都道府県の代表大学の入試偏差値)+ ε
※A:定数、α/β/γ/δ/ζ=係数(定数)、ε:誤差項

補正R2は0.7071と更に増えています。ただ、変数を個別に見ると、今回追加した都道府県の代表大学の入試偏差値のP-値は20%を超えており、相関していると言えません。地元を代表する国立総合大学の入試難易度(レベル)は、その都道府県から難関大学への進学者数には影響を与えていないようです。
4. 最後に
上記の分析から、東京一工・地帝・早慶の都道府県別の進学者数に重力モデルが当てはまり、「難関大学の進学者数は、大学の定員と都道府県の高3生徒数に比例し、出身都道府県との距離に反比例する」ことがわかりました。さらに、「対象大学の入試偏差値(難易度)に、進学者数は反比例する」こともわかりました。
全体としては、重力モデルが当てはまるようですが、個々の大学の都道府県別の進学者数を見ると、興味深いデータも見られます。例えば、このデータは東北大と名古屋大の宮城県・愛知県の出身者のデータセットを抽出したものです。
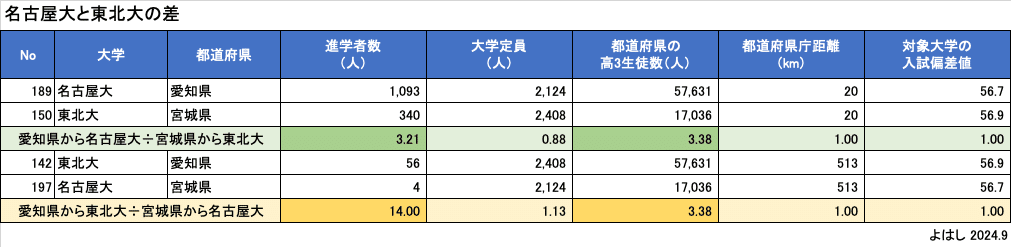
上の段は、名古屋大の愛知県出身者と東北大の宮城県出身者、いわゆる地元の旧帝国大への進学のパターンです。グリーンの行を見ると、都道府県庁距離は当然同じ(地元同士)なのですが、大学定員と対象入試偏差値もほぼ同じことがわかります。結果、それぞれの都道府県の高3生徒数の比率の約3倍(x 3.38)であることから、名古屋大進学者数は東北大の進学数の約3倍(x 3.21)となっています。
一方、下の段は出身地をクロスさせて、名古屋大の宮城県出身者と東北大の愛知県出身者を比較しています。イエローの行を見ると、地元比較と同様に都道府県庁距離、大学定員、入試偏差値は同じですが、進学者数と都道府県の高3年生が比例していないことがわかります。
愛知県は宮城県の約3倍(x 3.38)の高3生徒がいるで、愛知県から東北大への進学数は、逆方向の宮城県から名古屋大への進学数の約3倍のはずです。ところが、実際の逆方向の進学数は14倍(x 14.00)しています。愛知県から東北大は流出過多、宮城県から名古屋大は流入過小です。言い換えると、名古屋大は東北大よりも他の類似地域の学生を集める何かが不足していることになります。
では、この不足しているの何かは何なのでしょうか? 次回は重力モデルの残差を分析しながら、定員・高3生徒数と距離と偏差値では説明できない大学が進学者に与える影響を分析してみます。
