
キャッシュメモリを有効利用する方法
超高性能プログラミング技術のメモ(8)
超高性能プログラミング技術を忘れないように記録しています。
今回は、汎用メモリ・キャッシュ・レジスタの記憶階層を有効活用するためのループブロッキング技術を記述していきます。
ここでは、多次元配列を対象とします。多次元配列の場合、メモリ上のデータの配置順序とアルゴリズム上のデータの使用順序が異なること多々あります。そうすると、ストライドアクセス(データを飛ばし飛ばし使用する)や間接参照(リストから読み込んだインデックスのデータにアクセス)など、CPUが先読みしてキャッシュにプリフェッチしたデータを無駄にするケースが頻発するためです。多次元配列でも一番簡単な2次元配列(行列)の場合を考えます。
修正履歴
・2020/7/26 計算ミスを修正
ループ・ブロッキング
ループ・ブロッキングとは、簡単に言うと、二重ループのストリップマイニングです。結果として、4重ループになりますが、外側2ループをブロック選択ループ(アウターループ)に、内側2ループをブロック内走査ループ(インナーループ)にすることで、計算に使用するブロックを限定することができます。
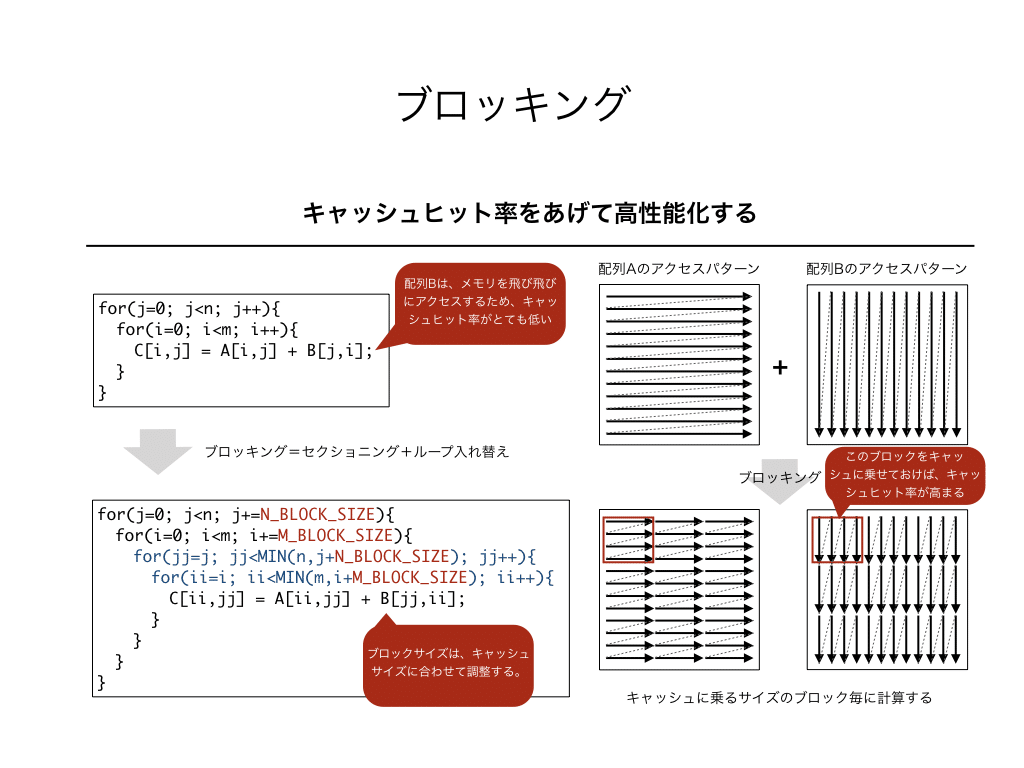
上図は、ブロッキングの擬似コードと配列アクセスパターンです。配列Aのアクセスパターンがメモリ配置順序に沿っているとすると、配列Bのアクセスパターンは常にストライドアクセスすることになります。(メモリ配置が逆の場合は、配列Aがストライドアクセスになります。)そのため、元のコードはキャッシュヒット率が常に低いことになります。
ブロッキングにより、1ブロックの計算に必要な配列Bのサイズを小さくすると、配列BのブロックがL1Dキャッシュ上に残り続けることになります。そうすると、B[jj,0]のロード時にキャッシュに先読みされた64Bのデータが、B[jj,1]の時に再利用され、メモリアクセスの回数が減少します。
したがって、M_BLOCK_SIZEとN_BLOCK_SIZEは、配列Bのブロック容量がL1Dのキャッシュサイズ32KBよりも小さくなるように設定しなければいけません。同時に、配列Aや配列Cの容量も必要です。配列A,B,Cの大きさは全てM*Nなので、M_BLOCK_SIZEとN_BLOCK_SIZEは、次の不等式が成立しなければいけません。
3*(M_BLOCK_SIZE*N_BLOCK_SIZE*8B) =< 2^15B (=32KB)
配列数3を4にしても不等式が成立すれば、3の場合も不等式が成立するので、簡単のために4にして計算します。
4*8*M_BLOCK_SIZE*N_BLOCK_SIZE <= 32*1024
--> M_BLOCK_SIZE*N_BLOCK_SIZE <= 1024 = 32*32
したがって、M_BLOCK_SIZE=32、N_BLOCK_SIZE=32あたりが妥当と考えられます。
パネリング
パネリングとは、多段ブロッキングのことです。多層化したキャッシュを有効利用するための技術で、ブロッキングで作られたブロック選択ループのさらに外側でパネル選択ループを作ります。

上図は、上でブロッキングしたアルゴリズムをさらにパネリングしたコードになります。
パネルサイズの計算方法を、ほぼブロックサイズの計算と同様ですが、今度はL2キャッシュの容量256KB以下になるようにします。そのため、下記のように不等式を計算します。
3*(M_PANEL_SIZE*N_PANEL_SIZE*8B) =< 256KB
--> 4*8*M_PANEL_SIZE*N_PANEL_SIZE =< 256*1024
--> M_PANEL_SIZE*N_PANEL_SIZE =< 8*1024 = 128*64
結果として、少し余裕を持たせてM_PANEL_SIZE=128、N_PANAL_SIZE=64に設定すると良いと考えられます。
L3キャッシュの最適化も考えるには、さらに外側にブロッキングを行います。サイズの計算も同様で、1コアあたりのL3キャッシュ容量の2MB以下になるように設定します。
3*(M_L3PANEL_SIZE*N_L3PANEL_SIZE*8B) =< 2MB
--> 4*8*M_L3PANEL_SIZE*N_L3PANEL_SIZE =< 2*1024*1024
--> M_L3PANEL_SIZE*N_L3PANEL_SIZE =< 64*1024 = 256*256
計算結果では、M_L3PANEL_SIZE=256、N_L3PANEL_SIZE=256あたりが良さそうです。
ループアンローリング
ループアンローリングとは、ループを展開する(処理を書き下す)ことです。異なる反復の処理をまとめて行う場合などに使用されます。
ここでは、パネリングの終わった上図のコードを考えます。パネリングは外側ループを考えましたが、今度は内側に注目します。最内ループの中の処理は、C[,]=A[,]+B[,]しかなく、せいぜい3レジスタしか使われません。x86_64アーキテクチャには、XMMレジスタが16個も実装されているのに、3個しか使わないのは効率的ではありません。
そこで、内側ループをアンローリングし、異なる反復の処理を同時に行うことにします。実際のアンローリングは、①内側ループをブロッキング、②ブロック走査ループを展開することで実行できます。①と②を実行すると、下図のようになります。

上図では、アンロールサイズを2にしましたが、一般的には次のように計算できます。前提として、ここで考えているアルゴリズムは、1反復で3レジスタ使用することとします。
N_REG_1LOOP*M_UNROLL_SIZE*N_UNROLL_SIZE =< 16 regs
--> 3 regs *M_UNROLL_SIZE*N_UNROLL_SIZE =< 16 regs
--> M_UNROLL_SIZE*N_UNROLL_SIZE =< 5.3
これより、M_UNROLL_SIZE*N_UNROLL_SIZE = 4になると良いことが分かります。これを満たすには、M_UNROLL_SIZE=1、N_UNROLL_SIZE=4という設定も可能ですが、次のベクトライズ(SIMD化)を考えると、2要素同時にロードできるにも関わらず、配列Aを1要素ずつロードしなければならず、あまり得策ではありません。逆に、N_UNROLL_SIZE=1とすると配列Bを1要素ずつロードしなければならず、同様に非効率的です。結果として、M_UNROLL_SIZE=2、N_UNROLL_SIZE=2が妥当な設定となります。もし、このサイズを越えた設定にすると、アルゴリズムに対してレジスタ数が不足し、スピル処理が必要になります。
以前の回で、アセンブラ命令を高性能化するには、ロード命令のデータ転送時間を稼ぐために無関係な処理を挿入すればよい、と書きました。この無関係な処理を増やす方法の答えが、このアンローリング技術になります。そもそも、別の反復で実行されていた処理は、アンローリングで一箇所にまとめても互いに独立に処理可能です。すなわち、アンローリングで一箇所にまとめられた処理1に対して処理2は無関係な処理になっています。したがって、アンローリングサイズを大きくするほど、データ転送時間を隠すことが可能になります。
ベクトライズ(SIMD化)
アンロール後のコードは、複数の処理を行なっているため、おそらくどんなコンパイラもベクトライズ可能とは判断できません。しかし、アンロール後のコードでは、メモリ配置的に連続した近接要素ばかりを使って計算が行われています。メモリ配置が連続していれば、SIMD計算が容易に可能です。そこで、手作業でベクトライズ(SIMD化)を行っていきます。
ここでは、配列A,B,Cの左側の添え字がメモリ配置の連続方向と仮定します。すなわち、A[i,j]とA[i+1,j]はメモリ上隣同士に配置されていると考えます。このように連続的に配置されたデータは、倍精度実数の場合、SSE命令なら2要素、AVX命令なら4要素を1回のロード命令(LD)でロードすることができます。上記のコードでは、配列Aが4要素、配列Bが4要素の計8要素を4命令でロードすることができます。

配列Aと配列Cは1つの式では同じ要素を使っていますが、配列Bは別の位置の要素を使用しています。そのため、ロードした状態のまま、加算を計算することはできません。そこで、配列Bの要素を入れ換えたベクトル(XMM8,XMM9)を作ります。作り方は、XMM4とXMM5の第1要素同士と第2要素同士を、それぞれ一つのベクトルとします。
こうすることで、配列Aの要素が入ったXMM0とXMM1、配列Bの要素が入ったXMM8とXMM9を1命令で2要素ずつ加算することができ、ベクトライズ(SIMD化)できたことになります。
SIMD化によって使用するレジスタ数は減ってしまいます。そのため、アンローリングサイズの計算は、実際にはSIMD化も考慮した計算を行う必要があります。
まとめ
今回は、記憶階層(汎用メモリ・キャッシュ・レジスタ)を有効活用するためのブロッキング技術を書きました。これは、CPUに搭載された資源を最大限活用するための技術です。ブロッキングは、高性能化に必須の技術になります。
