
演算とメモリ転送のオーバーラップ
超高性能プログラミング技術のメモ(12)
技術を忘れないようにメモしています。
今回から、浮動小数点演算の話に入りたいと思います。高性能化のポイントは、「レジスタスピルやパイプラインハザードを回避しながら、ロード命令のメモリ転送中に浮動小数点演算を同時実行させてしまうか」になります。
命令数のカウント
ここでは、複数のベクトルの内積を計算する擬似コードを考えてみましょう。
double* inner_product(unsigned int n, unsigned int l,
const double** x1, const double** x2,
double* y){
const double* z1[l] = x1;
const double* z2[l] = x2;
for( unsigned int k=0; k<l; k++ ){
for( unsigned int i=0; i<n; i++ ){
y[k] = y[k] + z1[k][i] * z2[k][i];
}
}
return y;
}このコードのループ最深部のメモリ転送命令と演算命令の個数を数えます。
ロード命令:3個・・・y[k], z1[k][i], z2[k][I]
ストア命令:1個・・・y[k]
加算命令 :1個・・・+
乗算命令 :1個・・・*
まずは、この最深部の命令数を減らすことを考えます。明らかに、y[k]は最深部に必要ないので、次のように変更することが可能です。
double* inner_product(unsigned int n, unsigned int l,
const double** x1, const double** x2,
double* y){
const double* z1[l] = x1;
const double* z2[l] = x2;
for( unsigned int k=0; k<l; k++ ){
double a = 0;
for( unsigned int i=0; i<n; i++ ){
a = a + z1[k][i] * z2[k][i];
}
y[k] = a;
}
return y;
}変数aは、スカラー変数なので、上手くコンパイラが解釈してくれると、コンパイル時にレジスタとして割り付けてもらえます。すると、y[k]に関する命令は、ループの最深部から外に出るので、次のように命令数は変わります。
ロード命令:2個・・・z1[k][i], z2[k][i]
ストア命令:0個
加算命令 :1個・・・+
乗算命令 :1個・・・*
このような変更によって、命令が削減された分だけ、通常は高速化されます。しかし、変数aがベクトルと解釈されなくなり、コンパイラのベクトル化(SIMD化)最適化を阻害する可能性があります。そのため、コンパイラによっては遅くなるかもしれません。
演算時間とメモリ転送時間の計算
次に、演算時間とメモリ転送時間を計算します。
Intel社の最適化マニュアルによると、演算命令の各命令のレイテンシー(処理が完了するまでの時間)と逆数スループット(次の処理に移行できるまでの時間)は次の通りです。
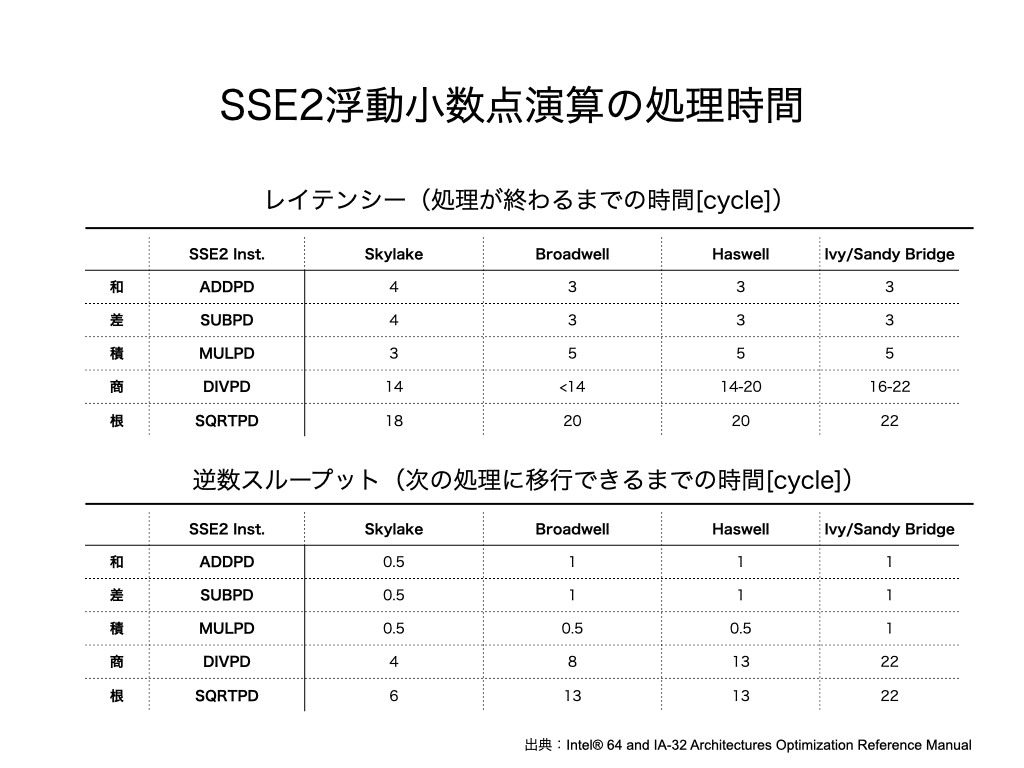
レイテンシーも逆数スループットもマイクロアーキテクチャによって違いがありますが、ここではSandy Bridgeマイクロアーキテクチャの場合で計算してみます。計算すると次のようになります。(上表から読み取ってください)
加算命令 :1個・・・レイテンシー3cycle、逆数スループット1cycle
乗算命令 :1個・・・レイテンシー5cycle、逆数スループット1cycle
ここで、単位cycleとは、CPUクロックが1回振動する時間です。実際の時間は、2.0GHzや3.6GHzといったクロック周波数で割ることで算出できます。
同様に、Intel社の最適化マニュアルには、メモリ転送時間はマイクロアーキテクチャごとに次のように記されています。

ここでは、全てのデータがL1キャッシュ上に乗っている理想的な状態を考えることにします。すると、メモリ転送命令のレイテンシーは次のようになります。逆数スループットは、最適化マニュアルを参照すると全て1cycleであることが分かります。
ロード命令:2個・・・レイテンシー8cycle、逆数スループット2cycle
ストア命令:0個・・・レイテンシー0cycle、逆数スループット0cycle
上記の疑似コードでは、データを取り出すロード命令が終わるまでは乗算*は実行できませんし、乗算が終るまでは加算+も実行できません。すなわち、ロード命令、乗算命令、加算命令を順番に実行する必要があります。したがって、ループ最深部の計算時間は、ロード命令、乗算命令、加算命令のレイテンシーを足し合わせた時間になります。
計算時間=ロード命令+乗算命令+加算命令
=8 cycle + 5 cycle + 3 cycle
=16 cycle
同様に、次の処理(ループの次の反復)に移行できるまでの処理時間は、逆数スループットを足し合わせた時間になります。
処理時間=ロード命令+乗算命令+加算命令
=2 cycle + 1 cycle + 1 cycle
=4 cycle
さらなる高速化を考える
では、これ以上、高速化することはできないのでしょうか?
実は、さらに高速化することができます。そのために、例として使ったSandy Bridgeマイクロアーキテクチャのブロック図を見てみましょう。
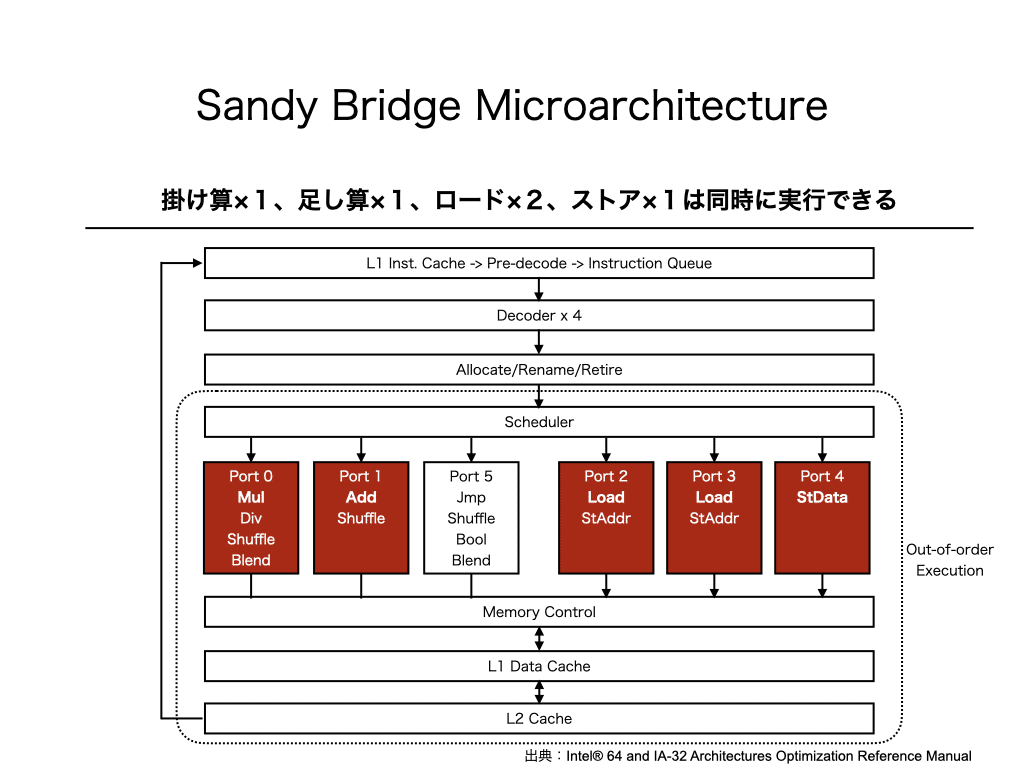
ブロック図に示されているように、現代のほとんどのCPUはOut-of-order実行が可能なように実装されています。Out-of-order実行は、命令を順序通りに実行するのではなく、順序を無視していくつかの命令を同時に実行する仕組みです。
どの命令を同時実行できるのは、Portに割り当てられた命令の種類を見ることで判明します。Sandy Bridgeでは、Port 0に乗算、Port 1に加算、Port 2とPort 3にロード、Port 4にストアが割り当てられており、これらはオーバーラップさせて同時に実行することが可能です。
計算順序を無視して、理想的にオーバーラップできると、次のようになります。
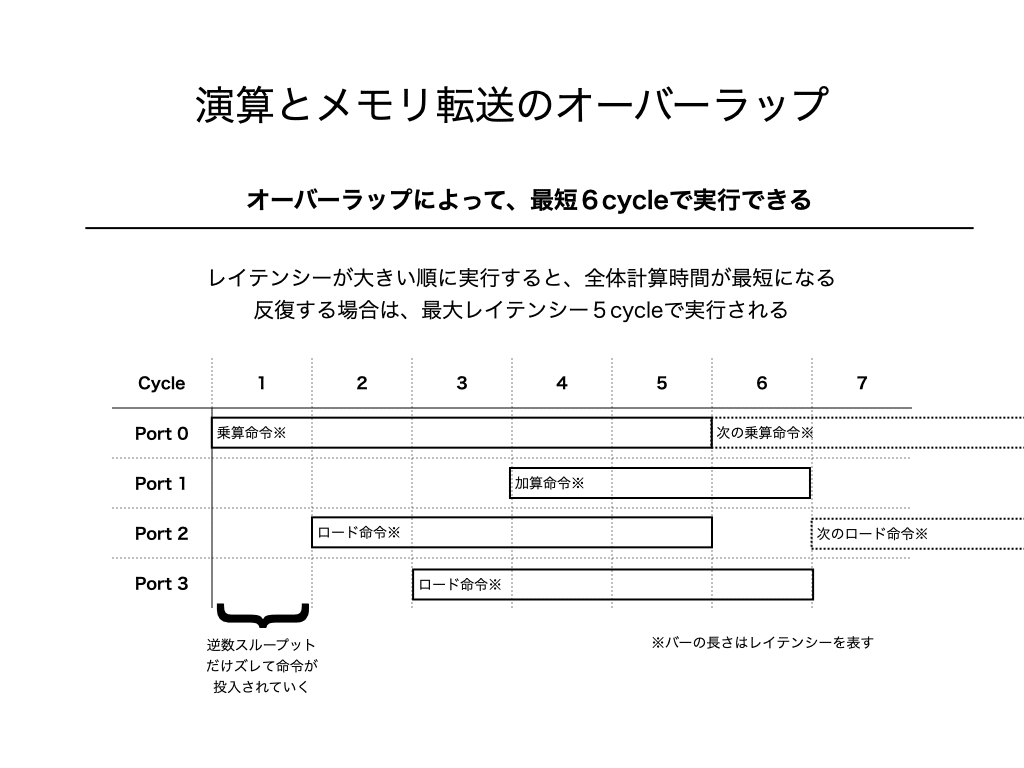
逆数スループットの時間だけズレて命令が発行されるので、レイテンシーが大きい順に命令を発行すると計算時間が最も短くなります。上図によると、乗算1個、加算1個、ロード2個の場合は、6cycleで実行することが可能と分かります。すなわち、16cycle→6cycleと2.67倍(=16/6倍)だけ高速化できる余地があることを示しています。
ループによる反復処理がある場合は、次の命令を6cycle目に発行できるため、実質的に5cycleで計算できることになります。つまり、3.2倍(=16/5倍)程度の高速化が見込めます。
オーバーラップさせるには?
しかし、実際には、内積計算には計算順序があり、上記のような理想的なオーバーラップはできません。計算に使用するデータが届く前に、計算を実行することはできないためです。
では、どうすればオーバーラップできるでしょうか?
1つの数式の計算では計算順序を無視することはできないため、依存関係のない複数の数式を同時に計算する方法を考えます。この時、使うのがループアンローリング技術です。
参考:
超高性能プログラミング技術のメモ(8)−メモリブロッキング技術
double* inner_product(unsigned int n, unsigned int l,
const double** x1, const double** x2,
double* y){
const double* z1[l] = x1;
const double* z2[l] = x2;
for( unsigned int k=0; k<l; k++ ){
double c1 = 0;
double c2 = 0;
double c3 = 0;
double c4 = 0;
for( unsigned int i=0; i<n; i+=4 ){
c1 = c1 + z1[k][i ] * z2[k][i ];
c2 = c2 + z1[k][i+1] * z2[k][i+1];
c3 = c3 + z1[k][i+2] * z2[k][i+2];
c4 = c4 + z1[k][i+3] * z2[k][i+3];
}
y[k] = c1+c2+c3+c4;
}
return y;
}上記のコードは、簡単のために端数処理を省略しているので、実際に使う場合には、端数処理を加えてください。
このコードでは、c1,c2,c3,c4の計算の間には依存関係がありません。そのため、例えば、c1の計算で必要なロード命令と、c2の計算で必要な乗算や加算はオーバーラップさせることができます。
しかし、c1の計算の中で必要なロード命令と乗算・加算には、計算順序に由来するロード→演算型の依存関係(RAWハザード)があるままです。これを理想型のように、乗算を発行してからロード命令を発行する形に持っていくために、まずは演算命令とロード命令を明確に分離します。
参考:
超高性能プログラミング技術のメモ(3)−レジスタスピルとパイプラインハザード
double* inner_product(unsigned int n, unsigned int l,
const double** x1, const double** x2,
double* y){
const double* z1[l] = x1;
const double* z2[l] = x2;
double c1,c2,c3,c4;
double a1,a2,a3,a4;
double b1,b2,b3,b4;
double d1,d2,d3,d4;
for( unsigned int k=0; k<l; k++ ){
c1=0; c2=0; c3=0; c4=0;
for( unsigned int i=0; i<n; i+=4 ){
a1 = z1[k][i ];
a2 = z1[k][i+1];
a3 = z1[k][i+2];
a4 = z1[k][i+3];
b1 = z2[k][i ];
b2 = z2[k][i+1];
b3 = z2[k][i+2];
b4 = z2[k][i+3];
d1 = a1 * b1;
d2 = a2 * b2;
d3 = a3 * b3;
d4 = a4 * b4;
c1 = c1 + d1;
c2 = c2 + d2;
c3 = c3 + d3;
c4 = c4 + d4;
}
y[k] = c1+c2+c3+c4;
}
return y;
}この時、注意すべき点は、一時変数として用意した変数a1~a4, b1~b4, c1~c4, d1~d4の総数をレジスタ数に以下にしておくことです。そうすると、レジスタスピルが発生せず、コンパイラが一時変数を全てレジスタに割り当ててくれる可能性が高まります。x86_64マシンであれば、xmm/ymmレジスタが16個使用できるため、16個の一時変数は、おそらくレジスタに割り当てられます。
参考:
超高性能プログラミング技術のメモ(3)−レジスタスピルとパイプラインハザード
このままでは、単に計算を分解しただけなので、特にオーバーラップは起こりません。これのループ最深部を、理想型通りに乗算から始まるように変更するには、ループずらし技術を適用します。
参考:
超高性能プログラミング技術のメモ(4)−パイプラインハザードの防ぎ方
double* inner_product(unsigned int n, unsigned int l,
const double** x1, const double** x2,
double* y){
const double* z1[l] = x1;
const double* z2[l] = x2;
double c1,c2,c3,c4;
double a1,a2,a3,a4;
double b1,b2,b3,b4;
double d1,d2,d3,d4;
for( unsigned int k=0; k<l; k++ ){
a1 = z1[k][0];
a2 = z1[k][1];
b1 = z2[k][0];
b2 = z2[k][1];
c1=0; c2=0; c3=0; c4=0;
d1=0; d2=0; d3=0; d4=0;
for( unsigned int i=4; i<n-4; i+=4 ){
c3 = c3 + d3;
c4 = c4 + d4;
a3 = z1[k][i-2];
a4 = z1[k][i-1];
b3 = z2[k][i-2];
b4 = z2[k][i-1];
d1 = a1 * b1;
d2 = a2 * b2;
d3 = a3 * b3;
d4 = a4 * b4;
c1 = c1 + d1;
c2 = c2 + d2;
a1 = z1[k][i ];
a2 = z1[k][i+1];
b1 = z2[k][i ];
b2 = z2[k][i+1];
}
c3 = c3 + d3;
c4 = c4 + d4;
a3 = z1[k][n-2];
a4 = z1[k][n-1];
b3 = z2[k][n-2];
b4 = z2[k][n-1];
d1 = a1 * b1;
d2 = a2 * b2;
d3 = a3 * b3;
d4 = a4 * b4;
c1 = c1 + d1;
c2 = c2 + d2;
c3 = c3 + d3;
c4 = c4 + d4;
y[k] = c1+c2+c3+c4;
}
return y;
}上記コードでは、ループ最深部からRAWハザード型の依存関係(ロード→演算)が半分なくなりました。これにより、次のような理想型の命令順序に並べることができます。
double* inner_product(unsigned int n, unsigned int l,
const double** x1, const double** x2,
double* y){
const double* z1[l] = x1;
const double* z2[l] = x2;
double c1,c2,c3,c4;
double a1,a2,a3,a4;
double b1,b2,b3,b4;
double d1,d2,d3,d4;
for( unsigned int k=0; k<l; k++ ){
a1 = z1[k][0];
a2 = z1[k][1];
b1 = z2[k][0];
b2 = z2[k][1];
c1=0; c2=0; c3=0; c4=0;
d1=0; d2=0; d3=0; d4=0;
for( unsigned int i=4; i<n-4; i+=4 ){
/* 1 */
d1 = a1 * b1;
a3 = z1[k][i-2];
b3 = z2[k][i-2];
c3 = c3 + d3;
/* 2 */
d2 = a2 * b2;
a4 = z1[k][i-1];
b4 = z2[k][i-1];
c4 = c4 + d4;
/* 3 */
d3 = a3 * b3;
a1 = z1[k][i ];
b1 = z2[k][i ];
c1 = c1 + d1;
/* 4 */
d4 = a4 * b4;
a2 = z1[k][i+1];
b2 = z2[k][i+1];
c2 = c2 + d2;
}
c3 = c3 + d3;
c4 = c4 + d4;
a3 = z1[k][n-2];
a4 = z1[k][n-1];
b3 = z2[k][n-2];
b4 = z2[k][n-1];
d1 = a1 * b1;
d2 = a2 * b2;
d3 = a3 * b3;
d4 = a4 * b4;
c1 = c1 + d1;
c2 = c2 + d2;
c3 = c3 + d3;
c4 = c4 + d4;
y[k] = c1+c2+c3+c4;
}
return y;
}上記のコードでは、ループ最深部に全く依存関係のない乗算、ロード×2、加算のセットが4つできました。依存関係が全くないので、この乗算、ロード×2、加算の命令群はCPUの中でオーバーラップされ、同時実行されます。
さらに高速化するには
最後のコードは、残念ながら、コンパイラがベクトル化(SIMD化)できません。そのため、ベクトル処理を利用する形に自分で書き直す必要があります。しかし、コンパイラの最適化機能は役に立たないため、直接アセンブリ言語で書き直す必要があります。とはいえ、最後のコードは、一行がアセンブリ1命令に1対1対応しているので、それほど難しくはないでしょう。
参考:
超高性能プログラミング技術のメモ(7)−ストリップマイニング
超高性能プログラミング技術のメモ(8)−メモリブロッキング技術
終わりに
最初のコードと最後のコードを見比べてみると、複雑化し、人間には理解し難いコードになっていることが分かります。しかし、最後のコードは、コンピュータには理解しやすいため高速化されます。「人間に優しいシンプルコードは、CPUには優しくない」ことを覚えておいて欲しいと思います。
