
第16話 ニューラルネットワークを学ぶ -活性化関数の正体-
ディープラーニングの実装を目指して、ニューラルネットワークを勉強中です。
段々とアルゴリズムのコアに近づいてきて学習が楽しくなってきました。
さて、この回の内容は次のとおりです。
・ニューラルネットワークで扱う問題の種類(回帰と分類)
・活性化関数の正体
(ステップ関数、シグモイド関数、tanh、ReLU、Leaky ReLu、恒等関数、ソフトマックス関数)
今回の主役は活性化関数。
ニューロンモデルの核心部なのに「追々学習します。」と先延ばしにされてきた部分です。(やっとたどり着いた)
種類が多いですがニューラルネットワークの重要な部分のはずなので頑張っていきますよ。
それでは学習のスタートです!
(教科書「はじめてのディープラーニング」我妻幸長著)
ニューラルネットワークで扱う問題の種類(回帰と分類)
ニューラルネットワークは所詮、何かの問題を解決するためのツールです。
ではニューラルネットワークがどういう問題に対して有効なのかというと、大きく分けて2種類あります。
それは回帰問題と分類問題です。以下にそれぞれについて、説明します。
回帰問題
今持っているデータから予測式を立てて、新たなデータをもらったときにその出力値を予測する問題です。
例えば、「これまでの株価の傾向から明日の株価を予測する。」といったことは回帰問題になります。
分類問題
与えられたデータを決められた枠に分類する問題です。
例えば、「手書きの文字を識別する。」ことは分類問題になります。
出力結果は離散値になります。
活性化関数の正体
ニューロンは活性化関数とよばれるものを持っており、これが入力信号に対してどのような出力をするか(発火の条件)を決定します。
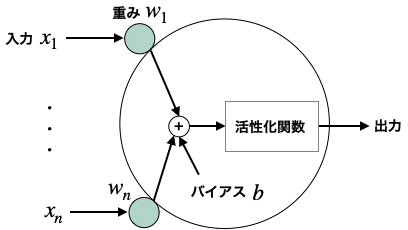
さて、活性化関数の正体はどのようなものでしょう。
なんと次のように色々な関数があるようです。
・ステップ関数
・シグモイド関数
・tanh
・ReLU(ランプ関数)
・Leaky ReLu
・恒等関数
・ソフトマックス関数
以降は、それぞれの関数がどのようなものかを説明していきます。
ステップ関数
0を境に階段(ステップ)状に出力が変化する関数です。
このようなコードで実装できます。

<この関数を使うメリット>
実装が簡単。
<この関数を使うデメリット>
0と1の中間状態を表現できない。
シグモイド関数
0〜1を滑らかに変化する関数です。
ステップ関数では0と1の中間を表現できませんが、シグモイド関数を使えばこの問題を解決できます。
右のようなコードで実装できます。

<この関数を使うメリット>
0と1を表現できる上に、微分が扱いやすい。
それはなぜかというと、シグモイド関数の導関数はシグモイド関数自体を使って計算できるからです。

ちょっと何を言っているのかわかりにくいと思いますが、ソースコードをみれば一目瞭然です。

tanh(ハイパボリックタンジェント)
-1〜1を滑らかに変化する関数です。
シグモイド関数と似ていますが、0を中心に対象になっている点が異なります。

数式は複雑ですが、numpyを使えば実装は超簡単です。
ちなみに導関数はこのようになります。

coshはハイパボリックコサインとよみます。
導関数のピークはシグモイド関数より大きいですね。
tanhは-1から、シグモイドは0からそれぞれ1に向かうので、tanhの方が傾きが大きいというわけです。
ReLU
ランプ関数ともよばれます。
ちなみにReLUは、rectified linear unitの略語で正規化線形ユニットという意味らしいです。
私はランプ関数と大学で習ったのでこちらの呼び方が好きです。

<この関数を使うメリット>
シンプルかつ層が多くなっても安定した学習ができる。
最近のディープラーニングでは主にこれが中間層の活性化関数として用いられる。
そして導関数がシンプル。
xによらず安定した値をとるのもこの関数の強みだそうです。
きっとこれが学習のときに役に立つ性質なのでしょうね。

Leaky ReLU
ReLUを改良したこんな感じのグラフです。

xが負の領域にあるときは0ではなく、小さな値をかけるようになっているのがReLUとの違いです。
<この関数を使うメリット>
ReLUでは出力が0になって学習が進まないニューロンが多数出現するdying ReLUという現象が起こる。
この関数を使えばdying ReLUを回避できると言われている。
ちなみにLeaky ReLUの導関数はReLUと同じくシンプルです。

恒等関数
出力=入力の関数です。
ニューラルネットワークの出力層でよく使用されるほか、連続的な数値を予測する回帰問題を扱うのにも適しているそうです。

ソフトマックス関数
正規化の関数で、分類問題を扱うのに適しているようです。
(正規化とは、データ等々を一定のルール(規則)に基づいて変形し、利用しやすくすること。by wikipedia)
例えば画像診断のAIがあったとして「この画像は犬2、猫1.5です」と出力されてもよくわからないですよね。
それを「この画像は犬の確率62%、猫の確率38%(合計は100%)」というように正規化してくれるのがソフトマックス関数です。
ちなみにこの解説はこちらのページを参考にさせていただきました。とてもわかりやすい!
ソフトマックス関数はこのような数式で表されます。

正直何をしているかよくわからないですよね・・・。
とりあえず正規化してくれる関数だと思っておけばよいでしょう。
以下は実装の一例です。

[1, 3, 5]という配列をソフトマックス関数で正規化してみました。
正規化すると5,3,1の順で値が大きくなり、合計は1になりましたね。
ソフトマックス関数は、正規化した要素の総和をとると必ず1になるという性質があります。
今回は「回帰と分類」「活性化関数」について学習しました。
活性化関数が色々あるのはわかりましたが、結局どれがいいんだ!?と思わずにはいられませんでした。^^;
まあきっと時々によって使い分けるのでしょう。
次回は待ちに待ったニューラルネットワークの実装に取り掛かります。
それではまた(^_^)ノシ
いいなと思ったら応援しよう!

