
第5話 NumPyを学ぶ -配列を演算・抽出・軸の入れ替えしてみたよ-
NumPyというPythonの拡張モジュール(ツール)について学んでいます。
今回はその2回目で、内容としては次のとおりです。
・配列の演算
・ブロードキャスト(形状が揃っていない配列の演算)
・要素へのアクセス
・配列の抽出(スライシング)
・軸の入れ替え(transpose、転置)
ではスタートです。
(参考図書 「はじめてのディープラーニング」我妻幸長著 2章Phythonの概要)
配列の演算
早速演算をやってみます。まずは簡単なものから。
配列のすべての要素に数字を足したり、かけたりしてみます。

配列に+3、*3としてあげるだけで、すべての要素に対して簡単に演算ができました。もちろん-3、/3もちゃんとできます。
ちなみに、NumPy配列ではなくPython配列だとどうなるか見てみましょう。

NumPy配列と全く違う結果になりました。
掛け算では、要素の掛け算じゃなくて元あった配列が増殖(?)しました。
足し算はそもそもできないんですね。(list型じゃないと連結できないというエラーメッセージが表示されています。)
次に配列同士の演算です。同じように足し算と掛け算をやってみます。

どちらも簡単にできました。
足し算はイメージどおりですが、掛け算は注意が必要です。
NumPy配列の掛け算は、同じ位置の要素同士の掛け算になります。
数学の行列の掛け算とは全く違いますね。
行列の掛け算の場合は、2*3の行列同士では掛け算できなくて、こんな感じの結果になります。
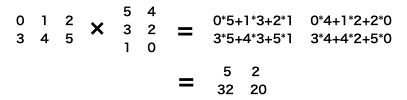
ブロードキャスト
なにやらテレビっぽい名前ですが、形状の異なる配列を計算するための方法ということです。
一体どうやってやるのでしょうか?
答えはシンプルで、足りない部分を拡張するようです。
でもルールが複雑らしく参考図書でも詳細は省かれています。

うーん、便利なのかな?使いどころがわからないw
勝手に配列形状変わっちゃったらプログラムを間違えたときに気がつきにくいかも。
要素へのアクセス
配列の各要素へのアクセスは、変数名[インデックス(指定したい番号)]でいけます。
これは他のプログラミング言語と一緒ですね。
具体例を示します。

2次元配列では、b[1]とすると2行目の要素すべてを指定できるのは便利ですね。
下のような感じで条件を指定してアクセスすれば、抽出もできます。

配列をインデックスに指定することもできます。
やってみましょう。

おや!?
fを代入することで置き換わってますが、置き換わった場所がイメージと違う・・・。
もう少し掘り下げてみます。

どうやら左と右のインデックスががっちゃんこしているようです。
一般化すると下式のようになってます。
g[np.array([x1, x2]), np.array([y1, y2])] = [g[x1, y1], g[x2, y2]]
とてもわかりにくいですね!
絶対に使わないやり方だと思いますw
スライシング
スライシングを使うと、配列の一部を取り出したり入れ替えたりできます。

こんなやり方でスライシングを用いた置き換えもできます。

さらに高い次元配列でのスライシングをみていきます。
試しに3次元配列の一部をスライシングで置き換えてみましょう。

いとも簡単に置き換えができました。
7章で登場する畳み込みニューラルネットワークでは、次元の多い配列のスライシングを多用するようです。
軸とtransposeメソッド
NumPyには座標軸という概念があり、次元の数だけ軸があります。
そして、transposeというメソッドを使えば軸を入れ替えることができます。
どういうことなのか具体例をみてみましょう。

2次元配列の行と列が簡単に入れ替わりました。
ちなみに転置(数学用語、Tというメソッド)を使っても同じことできます。
内部ではこういうことが起こっているようです。

3次元やもっと高次元でもtransposeメソッドは使えます。
例題をみていきましょう。


うーん・・・3次元になると入れ替わりのイメージが難しいですね^^;
ディープラーニングでは4次元以上のtransposeや転置がよく出てくるようです。
「データの方向が入れ替わるイメージを頭の中に描けるようにしておきましょう。」ってそんな簡単にできるかっ!
今回はNumPy配列の演算、抽出、軸の入れ替えを勉強しました。
次回はNumPyの関数について学習します。
それではまた(^_^)ノシ
よろしければサポートお願いします!いただいたサポートは書籍代等に活用いたします!
