第23話 バックプロパゲーションの理解に必要な知識 -勾配降下法- 詳細編

今回もニューラルネットワークの学習アルゴリズム"バックプロパゲーション"に必要な5つの知識のうち、3つ目の勾配降下法を学習していきます。

<バックプロパゲーションの理解に必要な5要素>
1　訓練データとテストデータ
2　損失関数
3　勾配降下法　←イマココ
4　最適化アルゴリズム
5　バッチサイズ

前回は勾配降下法の概要を説明しましたが、今回はもっと深入りした話です。具体的な内容は次のとおりです。

1  求めるべき勾配(前回のおさらい)
2  勾配を求める式のまとめ
3  今回のまとめ
4  (参考)勾配の導出過程

メインは2です。導出過程はかなり退屈なので、4に参考として載せます。

今回は偏微分をばんばん使います。
偏微分についての話はこちらにまとめたので興味のある方は是非。
・常微分と偏微分(第11話)
・全微分と多変数の連鎖律(第12話)

それでは学習をはじめましょう。
(教科書「はじめてのディープラーニング」我妻幸長著)

1  求めるべき勾配(前回のおさらい)

NNの学習のためには誤差を逆伝播していくのですが、その手順をおさらいします。

【逆伝播】
出力と正解値から損失関数を用いて誤差を算出する。
→誤差から出力層の重みとバイアスの勾配を求める。
→誤差から出力層の入力の勾配を求める。
→出力層の入力の勾配を中間層に伝播させる。
→これをもとに中間層の重み、バイアス、入力の勾配を求める。

このようなイメージです。

求めるべき勾配は次の6種類です。
<出力層>重み・バイアス・入力
<中間層>重み・バイアス・入力

これらの勾配を求める式をみていきましょう。

2  勾配を求める式のまとめ

6種類の勾配を一気にまとめます。
導出過程は後述しますので興味があればご覧ください。

この式だけでは意味不明だと思いますので図とともに解説します。

出力層ー中間層の逆伝播では、損失関数と活性化関数を伝播させ、それらの積であるδ_kが逆伝播して3種類の勾配を求めていきます。
手順にするとこのようになります。

1　損失関数の勾配を求める。
2　活性化関数の勾配を求める。
3　1と2を掛け合わせてδ_kを求める。(バイアスの勾配はこれでOK。)
4　3とy_jを掛け合わせて重みの勾配を求める。
5　3とw_jkを掛け合わせる。
6　5を全てのニューロンで行って総和を取り、入力の勾配を求める。

続いて中間層についてもみていきます。

中間層間の逆伝播の場合は、出力層の入力の勾配と活性化関数の積であるδ_jが逆伝播させ、その層の勾配を求めます。
手順にすると次のとおりです。

1　活性化関数の勾配を求める。
2　1と出力層で求めた入力の勾配を掛け合わせてδ_jを求める。(バイアスの勾配はこれでOK。)
3　2とy_iを掛け合わせて重みの勾配を求める。
4　2とw_ijを掛け合わせる。
5　4を全てのニューロンで行って総和を取り、入力の勾配を求める。

中間層がさらに増えた場合としても、この層の入力の勾配を1つ上の層に逆伝播してやれば良いので覚えるのはこれだけです。

3  今回のまとめ

今回は勾配降下法において重要な出力層と中間層の勾配を求める式を学びました。
導出過程を省略して先にまとめましたが、興味のある方は下の部分もご覧になってください。
出力層3つの勾配の導出過程だけでもみておくと勉強になると思います。
次回は回帰問題と分類問題における勾配の求め方について学習します。

それではまた(^_^)ノシ

4  (参考)勾配の導出過程

出力層の勾配
出力層において求めるべき勾配は次の3つがあります。
・重みの勾配
・バイアスの勾配
・入力の勾配

それぞれについて順番に導出していきましょう。

重みの勾配の導出
まずは、重みの勾配を導出していきましょう。
はじめに、中間層/出力層についての記号の添字とニューロン数を次のとおり定義します。

すると出力層のニューロンの信号は、次の図中の記号で表すことができます。
ここで重みは中間層・出力層どちらにも関係する変数なので、添字はjkとなっています。

ところで重みの勾配は、誤差Eを重みで偏微分することにより求まることを前回学習しました。

これを連鎖律により次のように式変形します。

ここで右辺の右側のu_kは、ニューロンの活性化関数への入力なので、このように式変形できます。

添字のqはΣを使用するためだけに登場したので意味はありません。
Σを展開したのが2つ目の式になります。
この式は項が多くて一見複雑ですが、よく見るとw_jkについての偏微分になのでw_jk以外は0となります。(w_jk以外は定数の微分のため0になる。)
しかもw_jkは微分すると1なので、最終的にこの式はy_jとなります。

式1の残りの右辺左側の部分についても見ていきましょう。
こちらも式変形により次のように表せます。

誤差Eを出力y_kで偏微分することは、すわなち損失関数の偏微分を意味します。
同様に、出力y_kを活性化関数の入力u_kで偏微分することは、すわなち活性化関数の偏微分を意味します。

以上の式1~3をまとめると、出力層の重みの勾配は次のように表せます。

これで重みの勾配の導出は完了です。

バイアスの勾配
続いて、バイアスの勾配を導出します。
やり方は重みのときと同様です。

バイアスの勾配は、誤差Eをバイアスで偏微分することにより求まることを前回学習しました。

これを連鎖律により次のように式変形します。

ここで右辺の右側のu_kは、ニューロンの活性化関数への入力なので、このように式変形できます。

一見難しそうでしたが、なんと1になりました。

式5の残りの右辺左側の部分については式3と同じです。
式3,5,6よりバイアスの勾配は次のように表せます。

入力の勾配
出力層では、1つ上流の中間層で重み/バイアスの勾配を演算するために、出力層の入力の勾配(=中間層の出力の勾配)を計算する必要があります。

出力層の入力の勾配は次のように表されます。

y_jは中間層の出力を意味しているので、出力層におけるすべてのニューロンの入力の総和と等しいというのがこの式の意味です。
添字のrはΣを使用するためだけに登場したので意味はありません。

重み/バイアス同様に、式8は次のように式変形できます。

したがって式8と9から、出力層における入力の勾配はこのようになります。

これで出力層において求めるべき勾配がすべて導出できました。
同じような式が何度も出てきてカオスになっていると思うので、今回の最後に必要なものをまとめます。

中間層の勾配
出力層に続いて中間層の勾配を導出していきます。
必要な勾配は、重み・バイアス・中間層への入力の3つです。
導出に必要なイメージ図と添字の記号を示します。

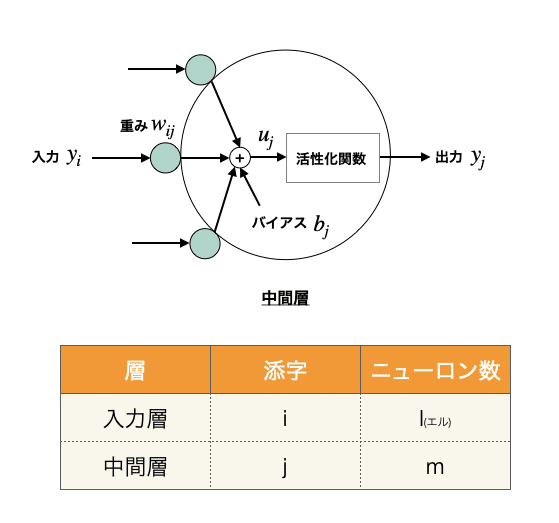
重みの勾配
出力層同様、重みの勾配は次のように表せます。

この式の右辺右側の分数を次のように式変形します。

さらに式11の右辺左側の分数を次のように式変形します。

式12と13より、式11は最終的にこうなります。
出力層のバイアスの勾配(式4)と似たような感じです。

バイアスの勾配
これも出力層と同じようにやっていきます。
まずバイアスの勾配は次のように表されます。

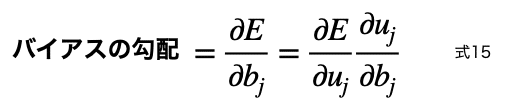
この右辺右側を式変形しましょう。こうなります。

したがって式15は式16により次の形になります。

中間層への入力
この層よりもさらに上に中間層がある場合には、次式を伝播させれば良いようです。(著者もめんどくさくなったのか導出過程は省略されている。)

興味があれば導出してみてください。(私はもう数式でお腹いっぱいなので諦めます。)

導出過程はこれで終わりです。
最後までご覧いただいた方、どうもありがとうございました！