第12話 ディープラーニングに必要な数学知識 -微分編 全微分・多変数の連鎖律-

前回に引続き、微分の勉強です。
微分は数学嫌いな方にとっては高い壁ですよね。

微分はディープラーニングではどうやら「勾配降下法」「バックプロパゲーション」で使うようです。
今回もソースコードなしですが、微分の勉強、頑張っていきましょう！
内容は次のとおりです。

・全微分
・多変数の連鎖律(合成関数の微分)

それでは今回の学習のスタートです！
(教科書「はじめてのディープラーニング」我妻幸長著)

全微分

変数が複数ある関数でも1変数しか微分しないのが偏微分でした。
これに対して、すべての変数について微分することを「全微分」といいます。
その名のとおりですね。

全微分は以下の式で表されます。

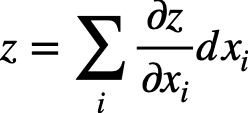
これだけでは意味不明ですね。
例を通して導出過程をみていきましょう。

2変数関数z=f(x,y)を全微分する例です。
xの微小変化をΔx、yの微小変化をΔyとすると、zの微小変化Δzは次のようになります。

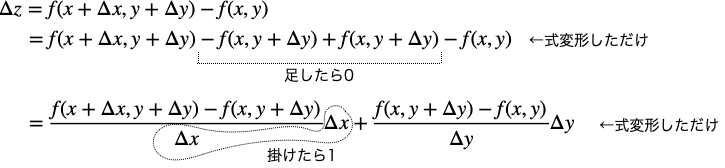
微小変化Δx、Δyを0に飛ばしてみましょう。

2変数の全微分をした場合、zをx,yの偏微分をしたものにそれぞれdx,dyをかければ良いことがわかりました。

これを一般化するとシグマの形で表すことができるというわけです。
(上の2変数の例に当てはめると、i = 2, x_1 = x, x_2 = yになる。)

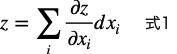
ニューラルネットワークは多くのパラメータを持つ多変数関数らしく、その微小な変化量を求めるときに全微分(結局は各変数の偏微分)が使われるようです。

多変数の連鎖律(合成関数の微分)

ちょいと複雑なので、簡単なところから入って一般化していきます。
まず、次のような合成関数について考えましょう。

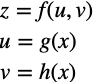
zはuとvの関数で、uとvはそれぞれxの関数です。(結局zはxの関数)
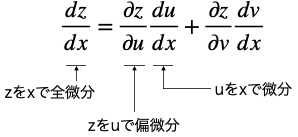
ここで、zをxで微分する(dz/dxを求める)と、全微分の式(式1) が適用できるので下式のようになります。

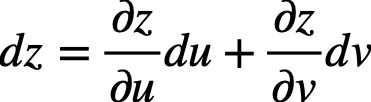
この両辺をdxで割ると次のようになります。

これを一般化する(今の中間関数2よりも大きくする)と下式になります。

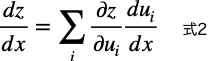
以上が1変数の連鎖律でした。
次に、以下のような2変数の合成関数の場合はどうなるでしょう。

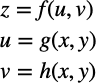
このときのzのxに対する偏微分とzのyに対する偏微分は、式2からこのようになります。

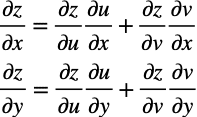
これらの式を一般化すると以下のような関係が成り立ちます。

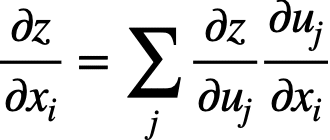
ここで、x_iはzを構成する変数の1つです。
さらにこの式は、ベクトルと行列積として表すことができます。

zが変数x_1, x_2, …, x_nの関数で、中間の関数がm個ある場合、このような表現になります。

これで多変数の連鎖律を一般化ができました。

ここまで頑張ってきたものの「ふーん、それで？」という感がいなめないのですが、これにはとてつもないメリットがあるようです。

それは行列積を用いれば、すべての変数による偏導関数を一度に導出できるということ。
ニューラルネットワークは多変数の合成関数なので、多変数の連鎖律を使って各パラメータが全体に及ぼす影響を求められるようになるそうです。

今回は、全微分と多変数の連鎖律について学習しました。
少々難解でしたね・・・。

前回、今回の2回に渡って微分を学びました。
微分の内容の理解と同時に、ディープラーニングと微分の関係もわかってきましたね。それは・・・

・ディープラーニングは多変数の合成関数である。
・どの変数(パラメータ)がどの程度全体に効くのかを求めるのに微分が必要。

ということ。
ディープラーニングを作るためには、微分は避けては通れない道のようです。
かくいう私は微分を完璧に理解しているわけではないですが、歩みを進めていこうと思います。

次回は正規分布について学習します。
それではまた(^_^)ノシ