第26話 バックプロパゲーションの理解に必要な知識 -バッチサイズ-

今回はニューラルネットワークの学習アルゴリズム"バックプロパゲーション"に必要な5つの知識のうち、5つ目のバッチサイズについて学習します。

<バックプロパゲーションの理解に必要な5要素>
・訓練データとテストデータ
・損失関数
・勾配降下法
・最適化アルゴリズム
・バッチサイズ　←イマココ

バッチサイズとは、重みとバイアスの更新を行う間隔のことで、ニューラルネットワークの学習効率に大きく影響を与えます。
今回はバッチサイズの概念と3種類の学習タイプについて勉強していきます。
具体的な内容は次のとおりです。

1. エポックとバッチ
2. バッチ学習
3. オンライン学習
4. ミニバッチ学習

それでは学習を始めましょう。
(教科書「はじめてのディープラーニング」我妻幸長著)

1. エポックとバッチ

ニューラルネットワーク の学習に使用するデータを訓練データと言いましたね。
訓練データには、入力と正解がペアになったデータ(=サンプル)がいくつもあります。
エポックとバッチは、訓練データをどれくらい使うかを数える単位です。

エポック
すべての訓練データを使用して学習することをエポックと呼び、すべての訓練データを1回使用したら1エポックと数えます。

バッチ
ニューラルネットワークでは、複数の訓練データを使用して学習させます。
この複数をデータのかたまりのことをバッチと呼び、バッチ内のサンプル数をバッチサイズと呼びます。
バッチ内のすべてのサンプルを使用してから重みとバイアスの更新が行われるので、「バッチサイズ＝重みとバイアスの更新間隔」ということもできます。
バッチサイズは、基本的に学習中ずっと一定です。

エポック、バッチ、バッチサイズの関係を図示するとこのようになります。

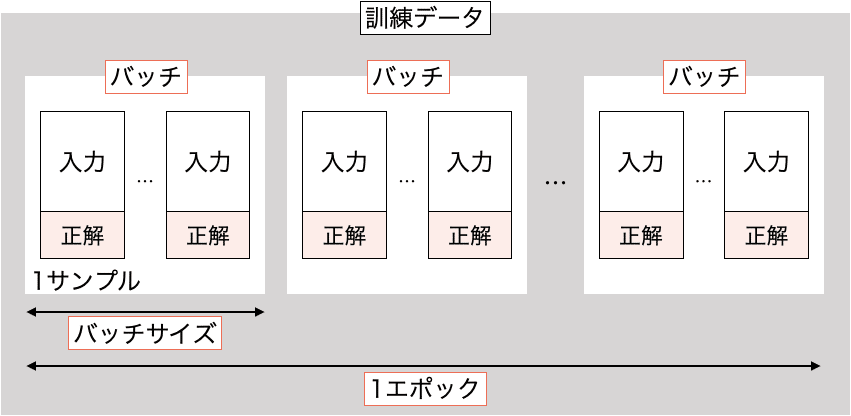
バッチサイズにより、学習のタイプを次の3つに分けることができます。
・バッチ学習
・オンライン学習
・ミニバッチ学習

2. バッチ学習

1エポックごとに全訓練データの誤差の平均を求め、重みとバイアスを更新することをバッチ学習といいます。
「バッチサイズ＝全サンプル数」となります。

例えば、訓練データのサンプルが1000個あるとしましょう。
バッチ学習ではバッチサイズが1000で、1エポックで1回重みとバイアスの更新が行われます。

メリット
一般的に学習は安定し、他の2つの学習タイプと比較すれば高速である。
デメリット
局所最適解に囚われやすい。

バッチ学習における誤差と重みの勾配は次のように表されます。

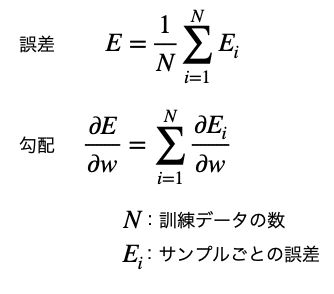
重みの勾配は、バッチ内の個々のデータごとに計算し、それを合計するということを意味しています。
この計算は、行列演算により一度に効率的に行うことができます。

3. オンライン学習

1サンプルごとに重みとバイアスを更新することをオンライン学習といいます。

先ほどと同じように例として、訓練データのサンプルが1000個があるとします。
オンライン学習ではバッチサイズが1で、1エポックでは1000回重みとバイアスの更新が行われます。

メリット
局所最適解に囚われにくい。
デメリット
個々のデータに振り回されるため安定性に欠ける。

4. ミニバッチ学習

訓練データを小さなかたまり(バッチ)に分割して、そのかたまりごとに重みとバイアスを更新することをミニバッチ学習といいます。
学習の間隔は、バッチ学習とオンライン学習の間になります。
これにより、両者のいいとこ取りができます。

またまた訓練データのサンプルが1000個の例を考えます。
ミニバッチ学習でバッチサイズを50にした場合は、1エポックでは20回重みとバイアスの更新が行われます。

メリット
バッチ学習よりもバッチサイズが小さく、ランダムにバッチを選択するため、バッチ学習と比較して局所最適解に囚われにくい。
オンライン学習よりもバッチサイズが大きいので、おかしな方向に学習するリスクが低減できる。

ミニバッチ学習における誤差と重みの勾配は次のように表されます。

バッチサイズが学習時間や精度に影響を与えることはよく知られているのですが、これを適切に設定するのは難しい問題で一般的には10〜100のバッチサイズを設定することが多いようです。

今回は、バッチサイズについて学習しました。
「バッチサイズ＝学習の間隔」で、これの大小によって学習の呼び方が3種類あることがわかりましたね。
結局どの学習を選択するの？ということになりますが、正確性を求めるならいいとこ取りをしたミニバッチ学習が良さそうな印象です。
求められる条件(正確性、演算時間など)によって、ケースバイケースで選択することになるのでしょう。

次回はニューラルネットワークの行列演算方法について勉強します。
どうぞお楽しみに。

それではまた(^_^)ノシ