
第28話 実装!回帰問題バックプロゲーション 実行結果編
第20話からバックプロゲーションについて学習してきましたが、実装するための準備(必要知識の習得)がついに整いました!
いよいよ待ちに待ったバックプロゲーションの実装です。
今回は回帰問題の学習の例として、バックプロゲーションによりニューラルネットワーク(以降NNと呼ぶ)がsin関数を学習する様子を観察します。
それでは学習を始めます。
NNの諸設定
今回は次のようなシンプルなNNで学習することとします。
入力層:ニューロン数1
中間層:1層、ニューロン数1(はじめは1で後から変える)
出力層:ニューロン数1
図示するとこのような感じです。

さらに、ネットワークの細部を次のように決めます。
中間層の活性化関数:シグモイド関数
出力層の活性化関数:恒等関数
損失関数 :二乗和誤差
最適化アルゴリズム:確率的勾配降下法
バッチサイズ :1
先ほどの図に書き加えるとこのような感じです。

今回は回帰問題を扱いますので、出力層は恒等関数、損失関数は二乗和誤差を選択します。
最適化アルゴリズムは一番シンプルな確率的勾配降下法を選択しました。
バッチサイズ1なのでオンライン学習と呼ばれるバッチ学習です。
全体のソースコード
パーツごとに解説して最後に全体のソースコードを載せようかとも考えましたが、最初に全体をお見せしちゃいます。
富士山を登る時も、山の全景が見えてる方が気持ちがいいですものね。(登ったことないけどw)
それではいきます。
(スクリーンショットの都合で画像が分かれていますが、ソースコードは連続してます。)





これをいきなり見せられてもよくわからないですよね^^;
わからないことはひとまずスルーして、これを実行するとどのような結果が得られるかを次にみていきましょう。
学習の結果
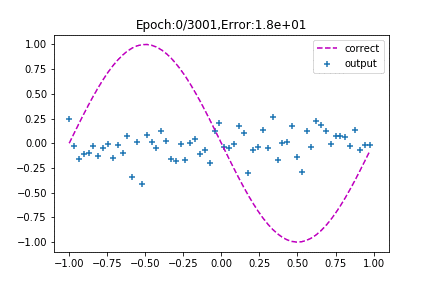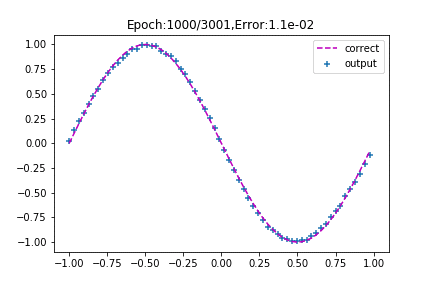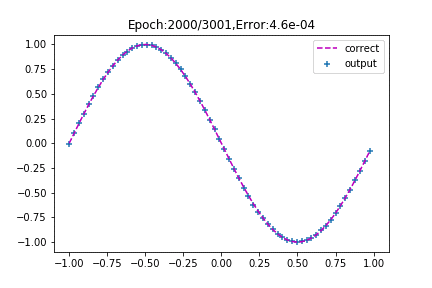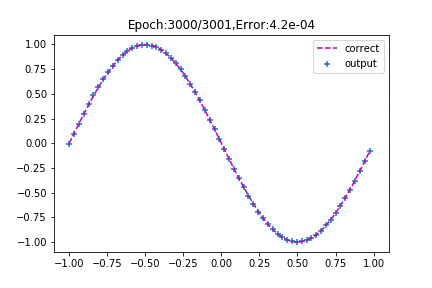
上のコードを実行すると、次のようなにNNが学習していく様子をgif画像を出力してくれます。(gifって便利ですね。)

output(NNの出力)がcorrect(正解)に近づいていますね。
これはバックプロゲーションによる学習のおかげです。
バックプロゲーションにより、誤差が小さくなるように各ニューロンの重みとバイアスが調整されています。
しかし、試行回数が増えてもsinカーブにフィットしませんね。
これは中間層のニューロン数が1であるために、NNの表現力が足りていないからです。
それでは中間層のニューロン数を3にしてみるとどうなるのでしょうか。
みていきましょう。
先ほどとは打って変わって、思わず「おお!」と声が出てしまうほどsinカーブにフィットしています。
ニューロン数が4つ(中間層3+出力層1)もあるので、人の手でここまで調整するのは大変ですが、バックプロゲーションならこのように自動でやってくれます。
バックプロゲーション、なんておそろしい子!(←わかる人いるかな?)
中間層のニューロンを増やしてみよう
中間層が3でこれなら、増やしたらもっと良くなりそう!と期待しちゃいますよね。
それではやってみましょう。
中間層を5つのニューロンにしてみました。

ん!?
初めは良くなったけど、学習の中盤以降はかえって悪くなったような・・・。
そんなときは誤差を定量的にみてみましょう。
上記では中間層のニューロン数を1,3,5にしてやってみましたが、他にも2,4,10を加えて、それぞれの誤差をプロットすることにします。
それではドン!
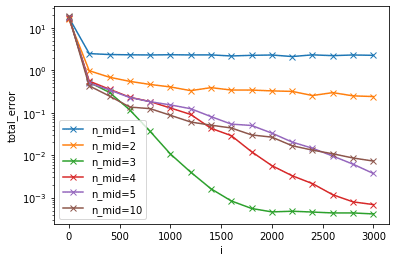
とても面白い結果になりました。
中間層のニューロン数が3の時、誤差が最も小さく、収束が最も早いですね。
ニューロン数が少ないと誤差は大きいまま収束してしまうし、ニューロン数が多くなるとかえって誤差の収束が遅くなることがわかります。
ニューロン数は多ければ良いということではないのですね。
ニューロン数をどのように設定するか、エンジニアリングセンスが問われそうです。
今回は回帰問題のバックプロゲーション実装例ということで、sin関数をバックプロゲーションで学習しました。
全体のコードとその実行結果を示して、バックプロゲーションによるNNの学習の様子が観察できましたね。
また、ニューロン数を変化させると学習がどのように変わるかも確認できました。
次回は今回すっ飛ばしたソースコードを解説します。
どうぞお楽しみに。
それではまた(^_^)ノシ
いいなと思ったら応援しよう!

