第27話 バッチ学習におけるニューラルネットワークの順伝播・逆伝播

今回は行列を用いたニューラルネットワーク(以降NNとよぶ)の演算について学習します。

実はこれまでにやっていたNNの演算は、層への入出力と正解をベクトルで表現していました。
しかし、前回学習した「バッチ学習」「ミニバッチ学習」ではベクトルではなく、行列を用いて演算することが必要になってきます。

そこで今回は、行列になるとNNの伝播はどうなるかを学習します。
具体的な内容は次のとおりです。

1. バッチ学習における行列(信号)の形式
2. バッチ学習における順伝播
3. バッチ学習における逆伝播

それでは学習を始めましょう。
(参考図書「はじめてのディープラーニング」我妻幸長著)

1. バッチ学習における行列(信号)の形式

おさらいで、NNの学習に使用する訓練データとバッチサイズの関係を次の図に示します。

これまで学習したNNは1サンプルごとの伝播だったのでベクトル表記でした。
バッチ学習においては、複数のサンプルが1セットになるので、複数のベクトルを束ねて1つの行列にします。
「ある層への入力」「ある層からの出力」「正解」の3種類の信号を行列形式で表すと次のようになります。

行列の行数は、バッチサイズと同じになります。
また、各行は訓練データのサンプルと対応しています。
例えば1バッチ目の9番目のサンプルだったとしたら、どこの行列の9行目でもこれに対応しています。(緑で示した行)
行列の列数は、各層のニューロン数と同じになります。

このようにバッチ学習における各層の信号を行列で表します。
行列化することにより、NNの伝播が容易に演算できるようになります。
(その理由は後述します。)

2. バッチ学習における順伝播

バッチサイズの信号を行列化した場合の順伝播をみていきましょう。
(信号がベクトルの場合については第15話を参照)

次の図に示すような層(入力数m、ニューロン数n)について考えます。

図1

このとき重み行列のサイズはm×nです。
また、バッチサイズをhとすると入力信号はh×mのサイズの行列になります。

ここでuの行列を求めていきましょう。
信号がベクトルの場合は、(入力と重みの行列積①)＋(バイアスのベクトル②)=(uベクトル③)であることをこれまでに学習しています。
では信号が行列(バッチサイズ)になるとどうなるのでしょうか。

まず、入力と重みの行列積①については次のようになります。

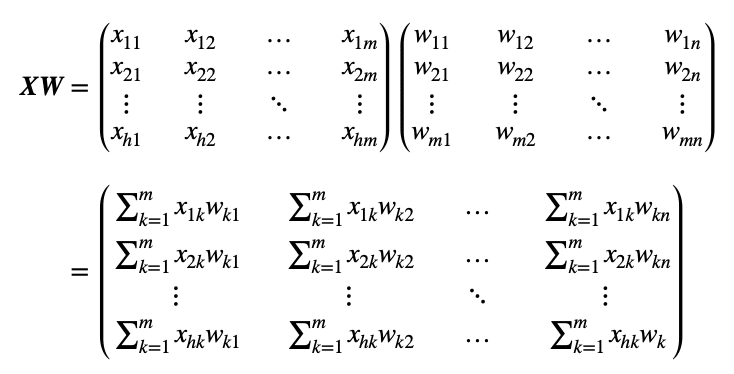
一見複雑ですが、行数はバッチサイズで、列数はニューロン数になっています。

続いて、バイアスのベクトル②についてみていきましょう。
バイアスはこのようなベクトルでした。

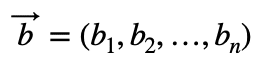
これをNumPyのブロードキャストにより、次のような行列にします。
(ブロードキャスト:行列のサイズを自動的に合わせること。詳細はこちら。)

①と②の行列がわかったので③の行列は次のようになります。

このUの行列を活性化関数fで処理すると、この層における出力Yを得ることができます。
Yのサイズはh×nです。(バッチサイズ×ニューロン数)

なにやら仰々しい形になりましたが、NumPyを使えば次のようにで実装することができます。その行数はなんと2行です！

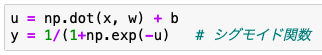
np.dotで行列xとwの行列積を求め、バイアスbを足します。(bはブロードキャストにより自動で行列化される。)
uの各要素を活性化関数で演算して、yの行列が得られます。

以上のように、順伝播は行列を用いて表すことができました。

3. バッチ学習における逆伝播

ベクトルでの逆伝播を次の図に示します。

図2

ベクトルの逆伝播ではδがニューロンを遡上させ、重み・バイアス・入力の勾配が求めました。
これらを行列化していきましょう。

行列化したδをΔと記すことにすると、Δは次のように表せます。

Δは層の出力Yと同じく、h×nの行列になります。(バッチサイズ×ニューロン数)

このΔを使って重みの勾配を行列化していきましょう。
まず、重みの勾配は1つ前の層の出力y_iとδを掛け合わせたものでしたが、1つ前の層の出力y_iというのは今の層の入力x_jのことなので次のように表せます。

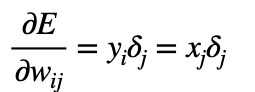
続いて、(前回学習しましたが)バッチ学習における重みの勾配は次式のとおりでした。

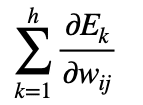
これらより、バッチ学習における重みの勾配は次のように表します。

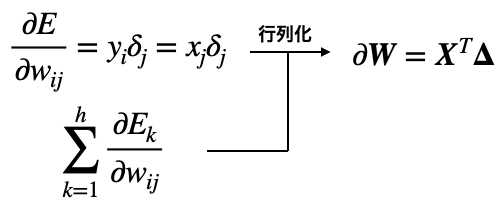
Tは転置を示す記号です。(転置ついてはこちら)
XとΔの行列積を計算するためには行列のサイズが合っている必要があるためこのように転置しています。
この行列のサイズはm×n(1つ上の層の出力数×ニューロン数)になっており、重み行列Wと一致します。
この計算をNumPyを使って実装すると次のようになります。

これで重みの勾配を行列化できました。
同様に、バイアスの勾配も行列化してみましょう。
さくっとまとめてこんな感じです。

これはNumPyで次のように実装します。
1行で書けてしまうなんて便利なんでしょう。

最後にこの層の入力の勾配を求めます。
入力の勾配は1つ上の層の出力y_i(=今の層の入力x_i)を使用して、バッチ対応した行列にすると次のように表せます。

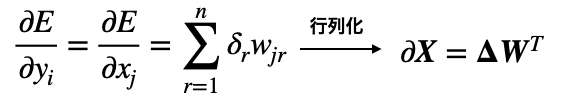
Wを転置しているのは、ΔとWの行列積をとるためです。
よくみると、各行は行列化する前の勾配の式と一致していますね。(添字がrではなくkになっているだけです。)
これをNumPyで実装すると次のようになります。

以上のとおり、バッチ学習における逆伝播を行列で表せることがわかりました。

今回はバッチ学習における順伝播・逆伝播を学習しました。
途中の過程は少々難解だったかもしれません。
しかし、最終的に伝播の式はシンプルな行列積で表され、その実装は驚くほどシンプルになることがわかりましたね。
細かな理屈はわかっていなくても、バッチ学習のNNの実装は簡単にできそうです。

次回は、回帰問題についてバックプロパゲーションを実装していきます。
どうぞお楽しみに。

それではまた(^_^)ノシ