
第32話 地味だけど利く ディープラーニングを成功させる小技8選
ディープラーニングとは、多層化したニューラルネットワークによる学習を指しますが、多層化することに伴い様々な問題が発生すること前回勉強しました。(詳細はこちらからどうぞ)
今回はそれらの問題点に対する対策を学習します。
問題点と対策をまとめると下表のようになります。

今回はこれらの対策について、1つずつ学習していきます。
ぶっちゃけ対策自体は地味です。(個人的にはドロップアウト以外は地味)
地味ですが、問題を解決するのには効果があります。
ディープラーニングの問題点を克服するために、色々と泥臭い工夫が必要ということが今回の学習を通してわかってきます。
それでは学習をはじめましょう。
(教科書「はじめてのディープラーニング」我妻幸長著)
1-1 バッチサイズの最適化
バッチサイズ(=学習のスパン)を最適化することで局所最適解にハマりにくくすることができます。
(詳細は第26話参照)

ミニバッチ学習を選んでおけば間違いがなさそうですね。
(バッチサイズをどれくらいに設定するかは経験や勘で決めていくことになりそうですが)
1-2 正則化
重みに制限をかけることを正則化といいます。
正則化することにより、重みが極端な値をとって局所最適解にトラップされるのを防ぐことができます。
代表的な正則化に次の2つがあります。
・重みの上限を設ける方法
・重みを減衰させる方法
ところで、なぜ制限をかけることを正則化と呼ぶのでしょう?
そう思ってWikipediaを見てみたらよくわからない数式が出てきたので、読むのを挫折しました…(興味があればこちらからどうぞ)
1-3 重みとバイアスの初期値
重みとバイアスの初期値は、学習の成否を握る大事なハイパーパラメータです。
(いきなりハイパーパラメータというnew wordが登場しましたが、これについては2-1で説明します。)
重みとバイアスの初期値は、ある程度小さい値でランダムにすることが望ましいとされています。(色々な研究があるようです。)
例えば次のような設定の仕方は、不都合が生じることがわかっています。
すべて同じ値で初期化 → ネットワークの表現力が失われてしまう
初期値が大きすぎる → 局所最適解にトラップされやすい
教科書(はじめてのディープラーニング、我妻幸長著)では、0を中心とした標準偏差0.01の正規分布を重みの初期値に採用しています。
第29話でランダム関数を使用して実装した理由がここで明かされました。(第29話はこちら)
2-1 ハイパーパラメータの最適化
学習を始める前に設定すべきパラメータをハイパーパラメータといいます。
たとえば、ニューラルネットワーク の層やニューロンの数、学習係数、重みとバイアスの初期値などはハイパーパラメータです。
反対にハイパーパラメータでないものは重みとバイアスで、これらは学習によって調整されるパラメータです。
ハイパーパラメータの最適化が必要な例としては、重みとバイアスの初期値(1.3項)のほかに中間層のニューロン数が挙げられます。
中間層のニューロン数を増やすとネットワークの表現力は増しますが、過学習が起きやすくなります。
ということは逆に、中間層のニューロン数を減らすとネットワークの表現力は減少しても、過学習が起きにくくなります。
表現力を確保しつつ、過学習は起こさないようにニューロン数を最適化することが求められるというわけです。
「ディープラーニングって機械でなんでもできるんじゃない?」と思っていた私にとって人間が決めるべきパラメータが意外に多くて、しかもそれが学習のパフォーマンスに大きな影響を与えるというのは意外な発見でした。
将来AIのせいで仕事がなくなると主張する人もいますが、AIを調整する人といった新たな職業も生まれる気がします。
2-2 早期終了
学習を途中で打ち切る手法を早期終了といいます。
学習を進めると、テストデータの誤差が途中から増加し過学習になってしまう場合や、誤差が停滞して学習がそれ以上進まなくなる場合があります。
このような状態になった場合に学習を打ち切ります。
そもそも「何回学習させるか?」と決めること自体が難しいので、学習の終了タイミングをアルゴリズムに任せるのが望ましいようです。
一般的には、テストデータの誤差の悪化が複数回見られ、悪化又は停滞の傾向が確認できた時点で学習を打ち切ります。
ただし、誤差が悪化又は停滞後に再び学習が進む場合があり、打ち切りは慎重に判断する必要があります。
2-3 データ拡張
訓練データのサンプル数が少ないと過学習が起きやすくなります。
狭い範囲のデータのみにネットワークが最適化されて、汎用性がなくなってしまうからです。
こういった場合に元あったサンプルを加工して、そのサンプルを新たなサンプルに加えることをデータ拡張といいます。(要は水増しです。)
例えば画像認識の場合、元のサンプル画像を加工(平行移動、回転、反転など)を行って、いろいろな画像を学習させることで過学習を防止します。
(ただし、過学習を必ず防ぐものではない。)
要は学習するデータは多い方が良いパフォーマンスを発揮できるということですね。「三人寄れば文殊の知恵」に近い考え方ではないでしょうか。
2-4 ドロップアウト
入力層、中間層のニューロンを一定の確率でランダムに消去する手法がドロップアウトです。
実装が比較的容易にもかかわらず、過学習の抑制に大きな効果があります。
ドロップアウトのイメージ図はこんな感じです。❌は消去されたニューロンを表しています。
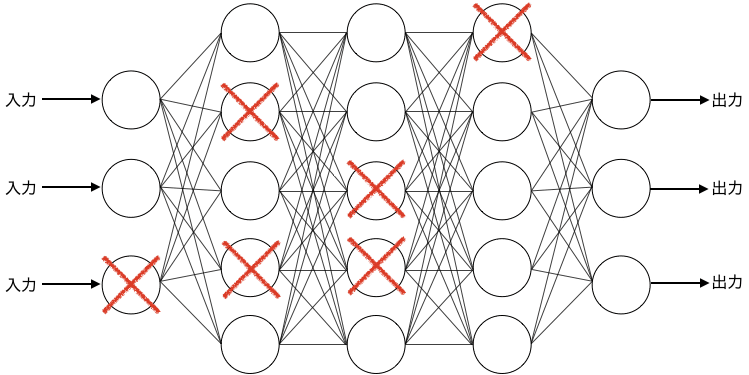
消去されるニューロンは、重みとバイアスを更新するたびに入れ替わります。
層のニューロンが消去されずに残る確率をpとした場合、中間層ではp=0.5、入力層ではp=0.8~0.9とする場合が多いようです。
テスト時には、このpの値を層の出力に掛け合わせて、学習時に減ったニューロンの分の辻褄を合わせます。
規模が大きいネットワークは過学習を起こしやすいのですが、ドロップアウトすることによりネットワークの規模が下がります。
しかも重みとバイアスの更新のたびにランダムにドロップアウトするので、1つの大規模ネットワークでありながら、あたかもサイズダウンしたネットワークを複数組み合わせたネットワークにすることができます。
これにより表現力を保ちつつ、過学習の抑制を実現します。
ドロップアウトは小さな計算コストで優れた結果を得られる手法であるため広く使われています。
ちなみに、このように複数のモデルを組み合わせることで結果の質が向上する効果をアンサンブル効果と呼びます。
「一人で達成できることには限界がある。」という人間社会に当てはまることはAI学習においても同じですね。
3-1 データの前処理
データを下ごしらえした方が、入力データをそのまま学習させるよりも、結果的に学習精度が上がったり、学習が高速化したりできます。
代表的な前処理は次の4つです。
・正規化
・標準化
・無相関化
・白色化
ぞれぞれについて解説しましょう。
正規化
データをある範囲(通常0〜1)に収まるように変換することを正規化と呼びます。
次の式によって正規化することができます。
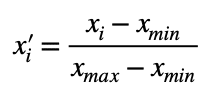
モノクロ画像の各画素は0~255の値をとりますが、正規化すると0~1の値になります。
参考までにPythonでの実装例はこんな感じです。

標準化
データの平均を0に、標準偏差(データのばらつきを表す尺度)を1に変換することを標準化といいます。
これによりデータの大部分は-1~1に収まります。(例外あり。)
次の式を用いて標準化します。
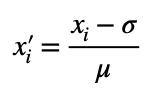
σはxの平均値、μは標準偏差です。
このPythonコード例は次のとおりです。

無相関化
例えば緯度、標高、平均気温などの地理データが集めたとして、この場合データの各成分には何らかの関係性があります。(標高が高い方が気温が低いといった関係など)
このようなデータの関係性のことを相関といい、相関を除去することを無相関化といいます。
無相関化すると、関係性が取り除かれたデータにすることができます。
白色化
データを標準化と無相関化を行うことを白色化と呼びます。
白色化するとデータは平均が0、分散が1となり、各成分の相関がなくなります。
学習に最適な入力データは、ほぼ一定の範囲に収まっていて、かつ偏りがなく互いに関係性がないものです。
この条件に当てはまらない場合は白色化することが望ましいです。
今回はディープラーニングの問題点を克服するための具体的な手法を学習しました。
対策の考え方は概ね理解できたのではないかと思います。
地味ですが良い結果を得るためには色々と対策が必要ということです。
あとはこれらをどのようにコードに落とし込むかですね。
次回は、ディープラーニングを用いてアイリス(アヤメ属の花)の品種を分類していこうと思います。
どうぞお楽しみに!
それではまた(^_^)ノシ
よろしければサポートお願いします!いただいたサポートは書籍代等に活用いたします!
