
第30話 実装!分類問題バックプロゲーション
新型コロナウイルス対応で会社の勤務時間が変わって、なかなか時間を取るのが難しくなってきましたが頑張っています!
今回は分類問題のバックプロゲーションの実装です。(バックプロゲーション=自動学習アルゴリズム)
ネットワークにx,y座標を入力し、sinカーブを境界線として領域をA,Bに分類する例をやってみます。
結論から言ってしまうとめっちゃキレイに分類してくれます、自動で!バックプロゲーション半端ないです。
ちなみに回帰問題のバックプロゲーション実装はコチラ→第28話、29話
それでは学習を始めましょう。
(参考図書「はじめてのディープラーニング」我妻幸長著)
ネットワークの諸設定
始めにニューロン数を決定します。
入力はx,y座標の2つが入ってくるので、入力層のニューロン数は2になります。
出力ではA,Bと2つに分類しますので、出力層のニューロン数は2となります。
中間層は自由に設定できますが、とりあえず6とします。
(あとで変えてみて、効果を確認します。)
ネットワークを図示するとこのような感じです。
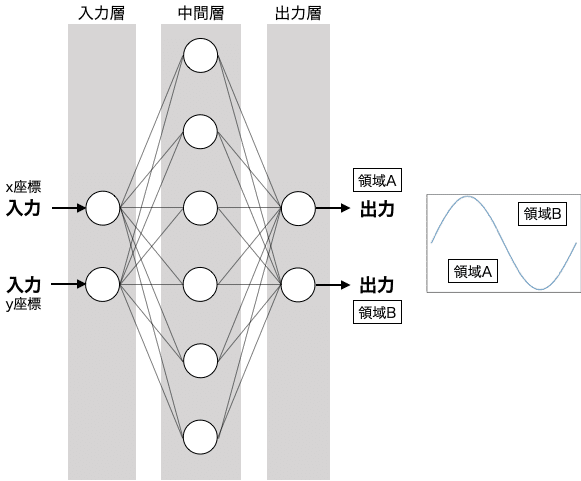
この他にも決めるべき条件があるので、図と一緒に示します。

第28話,29話では回帰問題のNNを実装しました。
それと今回のネットワークの違いは3つあります。というより3つしか違わないのでほとんど流用できます。
①出力層のニューロン数:複数 (回帰問題では出力層は1つ)
②出力層の活性化関数:ソフトマックス関数を使用 (詳細は第16話参照。)
③誤差を算出する損失関数:交差エントロピー誤差を使用 (詳細は第21話を参照。)
以上で実装するために設定すべき項目が全て決まったので実装に入ります。
出力層の実装
出力層のコードを示します。

① 初期設定(__init__、コンストラクタ)
初期設定を行う部分です。
上の層(中間層のニューロン数)をn_upper、出力層のニューロン数をnと定義し、これらを引数にして渡しています。
重みself.wはn_upper×nの行列で、バイアスself.bは要素数nのベクトルにします。
重みとバイアスの初期値はrandom.randnにより正規分布に従う乱数で、
wb_widthはその正規分布の広がり具合を決めるパラメータです。
(重みとバイアスをランダムに設定する理由は後日学習します。)
② 順伝播
順伝播をforwardメソッドと定義します。
入力ベクトルと重み行列の行列積にバイアスベクトルを足し合わせて、これを活性化関数に渡して出力を計算します。
出力層の活性化関数はソフトマックス関数です。
ソフトマックス関数の計算のところでsum関数の引数keepdims=Trueとすることで元の配列の次元が保たれます。
これによりこの行の計算結果は、バッチサイズ×1の行列になります。
逆伝播の演算でもこの時の入力x,出力yを使用するため、self.x,self.yという変数を使っています。
③ 逆伝播
逆伝播をbackwardメソッドと定義します。
正解tを引数として受け取り、deltaを計算します。
deltaは逆伝播のときにネットワークを遡上する変数です。
このdeltaを用いて重みの勾配grad_w、バイアスの勾配grad_b、この層の入力の勾配grad_xを計算します。
delta,grad_w,grad_b,grad_xの計算式は、下表のとおり第24回2項で導出した計算式です。

④ 重みとバイアスの更新
updateメソッドを定義し、ここで重みとバイアスの更新を行います。
最適化アルゴリズムは確率的勾配降下法ですので、これに従った計算式になっています。(確率的勾配降下法については第25話2項参照)

中間層の実装
次に中間層を説明します。
出力層とほとんど同じなので違うところを点線で示します。

中間層の活性化関数はシグモイド関数にしたので、順伝播のself.yと逆伝播のdeltaが出力層とは異なります。
全体のコード
それでは全体のコードを示します。
上記で解説した学習アルゴリズム以外に、学習・正解用データの生成する部分、繰返し学習を実行する部分、結果を表示する部分が加わります。
(画像はスクショの都合で分かれていますが、連続したコードとなっています。)






さて、これを実行すると結果は次のようになります。
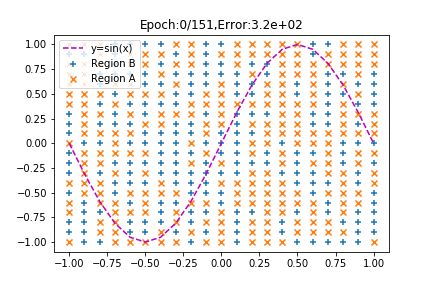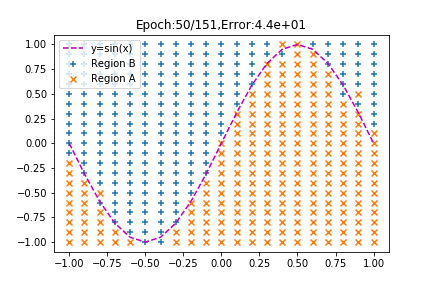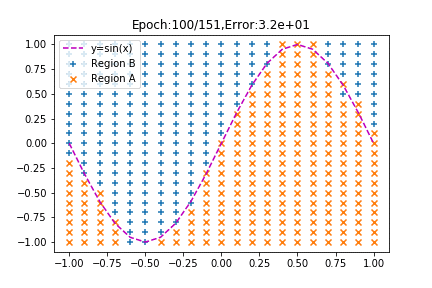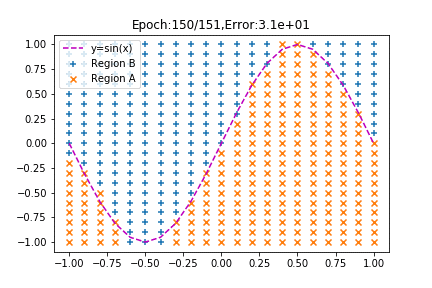
みてください、見事に分類されていく様子を!
学習が進むにつれてsinカーブを境にプロットが分かれていくではありませんか!(←テンション上がりすぎ!?)
中間層のニューロン数を比較してみた
中間層のニューロン数を6として実装しましたが、これを変化させると学習はどのように変わるのでしょうか。
結果を示します。
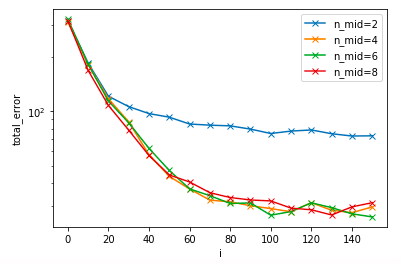
中間層のニューロン数が2と4以上の場合で誤差が違いますね。
後者の方が誤差が小さいので良いですが、4でも6でも8でもあまり変化はありません。
ニューロン数が大きいほど演算量が多くなりますので、今回の場合は4がベストチョイスなのではないかと思います。
今回は分類問題についてバックプロゲーションを実装しました。
sinカーブを境界にして、バックプロゲーションにより自動でデータを分類することができましたね。
次回からいよいよディープラーニングについての詳しい学習が始まります。
ディープラーニングの勉強を志しておよそ3ヶ月ようやくここまでたどり着きました!
学習が楽しみで仕方がありません。
それではまた(^_^)ノシ
よろしければサポートお願いします!いただいたサポートは書籍代等に活用いたします!
