第18話 3層のニューラルネットワークを実装する -回帰問題編-

今回は回帰問題(出力が連続的な値になる)について、入力層、1つの中間層、出力層の3層NNの実装を学習します。

具体的な内容は次のとおりです。
・3層のNN
・各層の実装
・全体の実装
・重みとバイアスの影響

前回は単一ニューロンの実装でしたので、ステップアップを実感できますね。

それでは学習を始めましょう。
(教科書「はじめてのディープラーニング」我妻幸長著)

3層のNN

次のような簡単な3層NNについて考えていきます。
・入力：2つ
・中間層：1層、ニューロン数2
図示するとこうなります。

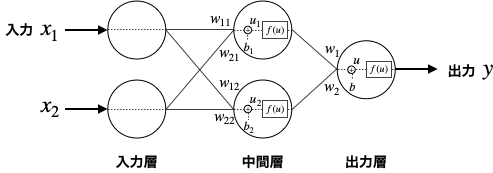
各層について解説します。

<入力層>
何も演算しないで中間層に信号を送ります。
<中間層>
入力層からの信号に重みを掛け、バイアスを加えます。(uを求める。)
これを活性化関数に入れて出力します。
重みの数ですが、この例だと入力は2つ、ニューロンは2つなので、中間層全体の重みは4つ(=2×2)存在します。
活性化関数にはディープラーニングではReLU関数(ランプ関数)がよく使用されるようですが、今回はシグモイド関数で実装します。
<出力層>
入力層からの信号に重みを掛け、バイアスを加えます。これを活性化関数に入れて出力します。
中間層との違いは活性化関数が恒等関数になることです。

(活性化関数がわからない方はこちらをどうぞ。)

各層の実装

各層を実装していきましょう。
入力層は何もしないので、実装するのは中間層と出力層です。

中間層
まずuを求める必要があります。
uは次の式で表せることをすでに学びました。(詳細はこちらを参照。)

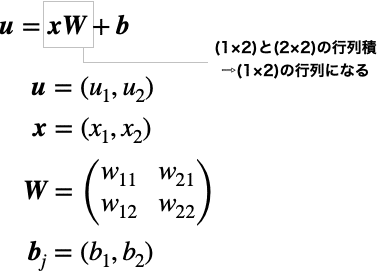
次にこのuをシグモイド関数に代入すれば良しです。
シグモイド関数は次の式で表されます。

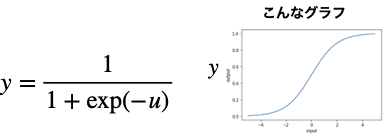
さあ、これらを実装するコードを書いてみましょう。
じゃじゃん！

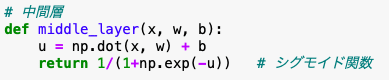
なんとまあシンプルなこと！
でもこれは演算部だけなので、別でx,w,bを渡してあげる必要があります。

出力層
出力層は、中間層と活性化関数が違うだけでした。
活性化関数は恒等関数なのでreturnのところだけを変えてやれば良いです。
恒等関数はこのような関数でしたね。

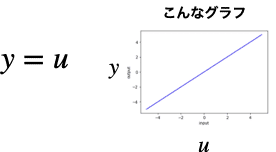
なのでコードを書くとこのようになります。

中間層よりも簡単に書けました。

全体の実装

コアとなる中間層と出力層のコードは書けたので、仕上げに全体を書きます。
残りの必要な部分は入力信号と、ニューロンの重みとバイアスですね。

入力信号は前回同様(-1.0, -1.0), (-1.0, -0.8), …(0.8, 0.6), (0.8, 0.8)という具合の100点の2次元データとします。
重みとバイアスは適当に決めました。(後ほど数値を変えてみます。)
ちなみに添字は、i：入力層、m：中間層、o：出力層を表しています。

それではソースコードの前半です。
変数と関数の定義を行なっています。

中間層、出力層のnp.dotは、行列積を表しています。
行列積を手計算するとめんどくさいのですが、np.dotを使えば一瞬で求められます。

続いてコードの後半です。
NNの演算とその結果の表示(ヒートマップ)を行なっています。

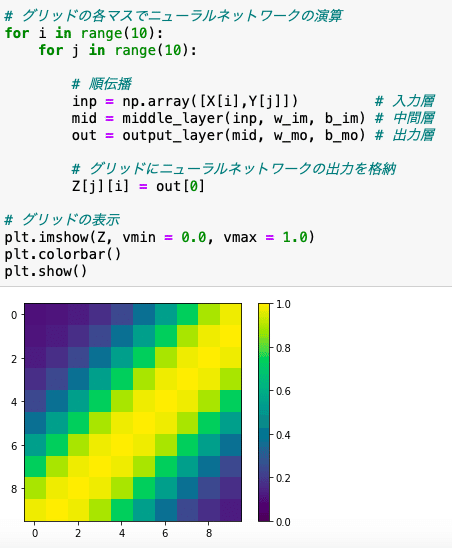
順伝播の入力層部では、入力信号を(1×2)の行列にしています。
中間層部のmiddle_layer関数には、入力信号、入力層-中間層間の重み行列、中間層のバイアスを引数として渡します。
同じように、出力層部のoutput_layer関数には、中間層の演算結果、中間層-出力層間の重み行列、出力層のバイアスを引数として渡します。
そして出力層の演算結果outをZ[j][i]に格納し、ヒートマップで表示しています。(outは(1×1)の行列なのでout[0]と代入しています。)

重みとバイアスの影響

重みとバイアスを変えて遊んでみました。

ニューロン単体に比べてヒートマップの模様を複雑にすることができました。
言い換えると、ニューロン単体よりも3層NNの方が表現できる能力が優れているということですね。
ということはつまり、NNの層・ニューロン数を増やすと複雑な出力を出せるようになり、高度な予測ができるようになるというわけですね。

ちなみにニューロン単体の出力結果の一例はこんな感じでした。(前回参照)

というわけで・・・
今回は3層のNN(回帰問題)について学習しました。
実装自体は行列積を用いて、中間層→出力層と順繰りに計算すれば良いことがわかりましたね。
そして層・ニューロン数が増えると複雑な出力が可能になるということもわかりました。

また今回は中間層が1つ、ニューロン数が2つでしたが、中間層が増えた場合は中間層→中間層→…→出力層とすればよく、ニューロンが増えた場合は重み行列とバイアスを増やしてあげれば良さそうなこともわかりました。

次回は3層NN(分類問題)について学習します。
それではまた(^_^)ノシ