第15話 ニューラルネットワークを学ぶ -順伝播の数式化-

AI(ディープラーニング)のプログラミングを作るために勉強をしています。

現在はニューラルネットワーク(ディープラーニングはこれを多重化したもの)について学習中で、前回はニューロンのモデル化を行いました。

今回はニューラルネットワークを数式に落とし込んでいきます。
具体的な内容は次のとおりです。

・ニューロンのネットワーク化
・重みの行列化
・信号のベクトル化
・順伝播の数式化

それでは学習のスタートです！
(教科書「はじめてのディープラーニング」我妻幸長著)

ニューロンのネットワーク化

ニューロン単体は多入力1出力システムで、ネットワークを組んでこそ真価を発揮するものでした。(興味があれば前回の内容をご覧ください。)
ニューロンの模式図はこのような感じです。

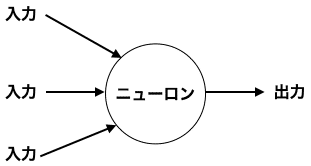
これをネットワーク化するとこのようになります。

少々込み入った図ですね。
入力層は3つのニューロン、中間層を3層にして各層は5つのニューロン、出力層は3つのニューロンといった例を描いてみました。
出力層以外のどのニューロンをみても、次の層のすべてのニューロンの入力につながっています。

ネットワークは3つの部分に分けることができます。

①　入力層
信号が入ってくる層です。
この層の各ニューロンは、演算しないで次の層のすべてのニューロンに信号を伝搬します。
②　中間層
演算を行う層です。
③　出力層
演算を行なって出力する層です。

また、信号が入力から出力へ流れることを「順伝播(じゅんでんぱ)」、その逆を「逆伝播」といいます。
逆伝播については、ニューラルネットワークの「学習」のときに勉強していきます。

さて、ここから先は順伝播を数式に落とし込んでいきますよ。

重みの行列化

まずは、簡単な例で次のような2層間の接続を考えてみます。
上の層に4つ下の層に3つのニューロンがあります。

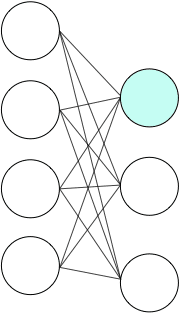
ここで水色に着色したニューロンについて考えていきます。

このニューロンの入力信号は、上の層のニューロンの数と同じ4つです。
そうなるとこのニューロンは、入力信号の数と同じ4つの重みを持つことになります。

同じように下の層の真ん中のニューロンをみてみると、このニューロンも重みが4つ存在します。

同じように一番下のニューロンも重みは4つあります。
したがって下の層の重みは、全部で12個あることがわかります(=上の層4つ × 下の層の3つ)。
これは行列を使って次のように表すことができます。

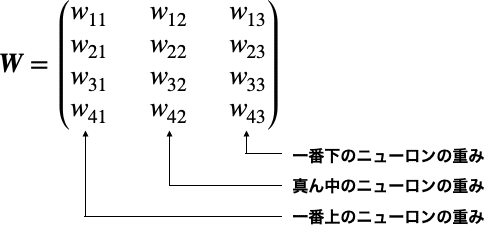
今のはニューロン数が(上の層,下の層)=(4,3)の場合でしたが、(上の層,下の層)=(m,n)の場合はこのようになります。

これで重みを行列で表すことができました。

信号のベクトル化

続いて信号についてみていきましょう。
j-1番目の層からm個の出力(j番目の層にとってはm個の入力)があり、j番目の層にn個のニューロンがある場合の模式図はこのようになります。
(絵の単純化のため各ニューロンからの出力はどこともつなげていません。)

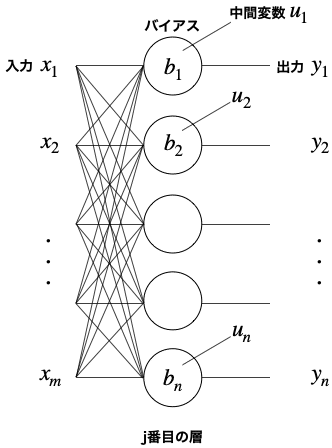
入力、バイアス、中間変数、出力のそれぞれを次のようなベクトルで表すことにします。(のちのち便利なので)

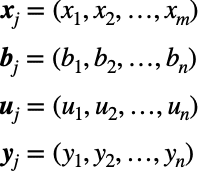
これで信号のベクトル化が完了です。とっても簡単！

順伝播の数式化

重みの行列化と各信号のベクトル化により、j層目の出力y_jは次式のように表せるようになります。

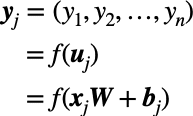
ここでfは活性化関数を表します。
fの()内は、ベクトルxと重み行列Wの行列積にベクトルbが加えられたものになっています。
式展開するとこのようなります。

これにより、j層目の出力y_jは最終的に次式で表せます。

以上により、2層のニューラルネットワークの出力を数式化できました。
層の数が3以上になった場合は、この式を用いて層1-2間、層2-3間・・・と順々に繰り返し計算すれば良いことになります。

ニューラルネットワークは、層の数が増えて規模が大きくなれば、より生物に近い認識・判断能力を持つことが可能になるようです。

というわけで、今回はニューラルネットワークの数式化を学びました。
添字がたくさん出てくるので一見複雑そうに見えますが、やっていることはさほど難しくはありませんでしたね。(それは私が行列に慣れているからか？)

ソースコードが出てこなかったので、ニューラルネットワークのプログラミング難易度は見えませんでしたが、数式を見た感じだとやればできそうなレベルだと感じました。

次回は「回帰と分類」について学習します。
それではまた(^_^)ノシ