
【数理的溢れ話21パス目】「単位元1」の定め方を巡る冒険(幾何学的アプローチと統計学的アプローチ)。
以下の投稿で述べた泡沫事象θ(Foamy Event,0<θ<2)の定義ですが、ネイピア数を用いてこんなふうにイメージする事も出来ます。
$$
Foamy(x) =
\begin{cases}
e^x & (x >0) \\
1 & (x = 0) \\
2-e^x & (x < 0)
\end{cases}
$$
これ(式1)を積分すると$${\int_0^2Formy(x)dx=2}$$。二で割って確率分布としてイメージする事も出来ます(式2)。
$$
Foamy(x) =
\begin{cases}
\frac{e^x}{2} & (x >0) \\
\frac{1}{2} & (x = 0) \\
\frac{2-e^x}{2}=1-\frac{e^x}{2} & (x < 0)
\end{cases}
$$

加法単位元0,や乗法単位元1を定める重要な局面ですね。それではどの様な応用が可能か順に見ていきましょう。
幾何学的アプローチ
式1から出発します、
正∞面体=球面座標系への拡張
虚数概念を導入してx=θi(-π<θ<+π)と置くと円環座標系を構築します(式3)。
$$
Foamy(x) =
\begin{cases}
e^{θi} & (θ >0) \\
1 +0i& (θ = 0) \\
2-e^{θi} & (θ < 0)
\end{cases}
$$
オイラーの公式$${e^{θi}=\cos(θ)+\sin(θ)i}$$を用いて
$$
Foamy(θ) =1-\cos(θ)+\sin(θ)i(-π<θ<+π)
$$


この実数軸1-cos(θ)、虚数軸sin(θ)iで構成される水平座標系にさらに垂直軸cos(φ)(-π<Φ<+π)を加えると球面座標系に拡張されますね(式4)。二次元表示だと垂直軸の+象限と-象限がピッタリ重なってその区別がつきません。
$$
Foamy(θ,φ) =1-\cos(θ)+\sin(θ)i+\cos(φ)i(-π<θ<+π,-π<Φ<+π)
$$



ああ、これはまさしく
コイン=正二面体(Regular Dihedron)
正四面体(Regular tetrahedron)
立方体(Cube)
正八面体(Regular Octahedron)
正十二面体(Regular Dodecahedron)
正二十面体(Regular Icosahedron)
に続く「第七のサイコロ」正無限面体(Regular infinitumhedron)=球面(Sphere)の定義に他なりません。ここでオイラーの多面体定理V(Vertex=頂点)-E(Edge=辺)+ F(Face=面)=対蹠(Antipodal)2を導入すると…
正二面体(コイン)のV-E+F=n-n+2(3<n<$${\tilde{∞}}$$)=2
正四面体のV-E+F=4-6+4=2
正六面体(立方体)のV-E+F=8−12+6=2
正八面体のV-E+F=6-12+8=2
正十二面体のV-E+F=20-30+12=2
正二十面体のV-E+F=12-30+20=2
正無限面体(球面)のV-E+F=$${\tilde{∞}}$$-$${\tilde{∞}}$$+2=2

正二面体(コイン)と正無限面体(についてはオイラーの多面体定理における多角形の場合(対蹠=0)すなわちV-E+F=0を用いてそれぞれ面を一個も備えない円弧および球面としても規定可能です。
トーラス体への拡張
実は上掲の「多角形としての正二面体(コイン)=円弧と正無限面体(球面)」は大半径Rと小半径rによって定められるトーラス体(単数形Torus, 複数形Tori)における両端でもあります。
大半径R=0の時…二重球面→正無限面体に対応
大半径R:小半径r=1:1の時…単位トーラス(Unit Torus)
小半径r=0の時…円弧→正二面体に対応

「大半径R=0の時は二重球面」…コインの表裏の様に球面の「表」「裏」をカウントしてる状態。普通はそうやって表裏を意識する必要がないので、例えば地球表面上位置を表す緯度(±90度)は軽度(±180度)の半分。
「単位トーラス(Unit Torus)」…多くの人にとって初見概念だと思いますが、実はコンピューターRPGによく出てくる「右端が左端に、上端が下端に連続するワールドマップ」に対応する位相空間。
群論では、ここでいう小半径r=0の場合を「1次元トーラス」、それ以外の場合を「二次元トーラス」と表現。さらにもう一次元加えた「三次元トーラス」は四元数(Quaternion)で表される空間となる。
「少なくとも部分的にはユークリッド座標系に従う次元が切れる」多様体(manifold)で考えるという事は、自明の場合として「屋根掛け法」の様な過去の遺物も含めこういう考え方も選択肢に入ってくるという事なんですね。
統計学的アプローチ
今度は式2から出発します。
ラプラス分布とコーシー分布
式2の水平軸のルベール内測度0~2を-∞~+∞の範囲に拡大したのがラプラス分布(Laplace Distribution)で、二重指数分布(Double Exponential Distribution)とも両側指数分布(Two-tailed Exponential Distribution)とも呼ばれます。
$$
Laplace(x∣μ,b)=\frac{1}{2b}e^{-\frac{|x−μ|}{b}}
$$
平均:𝜇(頂点の位置を定める)
尺度パラメータ:𝑏(裾の広がりを定める)
特に𝜇=0,b=1の時(中央値$${\frac{1}{2}}$$)を標準ラプラス分布という。
$$
Laplace(x∣0,1)=\frac{e^{-|x|}}{2}
$$

対応する「観察可能な自然分布」が実在するか咄嗟に思い浮かびません。機械学習アルゴリズムなどにおいて「外れ値をどう扱うか定める」主観分布として以下のコーシー分布(Cauchy Distribution)とセットで用いられます。
$$
Cauchy(x∣x_0,γ)=\frac{1}{πγ[1+(\frac{x−x_0}{γ})^2]}
$$
位置パラメータ:$${x_0}$$(中央値)
尺度パラメータ:𝛾(広がりを決める)
特に$${x_0}$$=0、𝛾=1の時を標準コーシー分布という。
$$
Cauchy(x∣0,1)=\frac{1}{π(1+x^2]}
$$
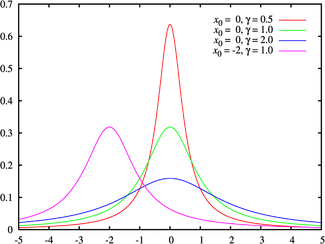
機械学習アルゴリズムにおいて、ラプラス分布とコーシー分布は、データの特性やモデルの要件に応じて異なる目的で使用されます。それぞれの分布がどのような特徴を持ち、どのような場面で適しているのかを見ていきましょう。
1. ラプラス分布(Laplace Distribution)
特徴
ラプラス分布(あるいは二重指数分布とも呼ばれます)は、尖った中心部と厚い裾(tails)を持つ対称分布です。ガウス分布(正規分布)に比べ、中心部での急な変化と、外側のデータ点が高い確率で出現することが特徴です。急激な変動があるデータや、スパース(疎な)データに適していることから、特定の機械学習タスクに有効です。
用途
L1正則化(Lasso):
ラプラス分布は、L1正則化の背後にある理論に関連しています。L1正則化では、コスト関数にパラメータの絶対値の和をペナルティとして追加します。これは、ラプラス分布の尖った形状がスパースな(0に近い)パラメータを選択する傾向があるため、特に特徴選択や疎なモデルに向いています。
例えば、Lasso回帰では、ラプラス分布の特性を利用して、多くの重みをゼロに近づけることで、重要な特徴量だけを残すことができます。
ロバストな回帰:
ラプラス分布は、データに外れ値が存在する場合にも有用です。正規分布と比較して、外れ値に対して強い影響を与えないので、ロバストな回帰手法に適しています。外れ値があっても、それらが大きな影響を与えにくいモデルを構築する際に使用されます。
ノイズモデル:
ラプラス分布は、ノイズが「スパイク状」であるようなデータに対して適しており、例えばデータが急激な変動やスパイクを含む場合のノイズのモデリングに使われます。
2. コーシー分布(Cauchy Distribution)
特徴
コーシー分布は、非常に厚い裾を持つ分布であり、平均や分散が定義されていないのが特徴です。これは、データが極端な外れ値を持つような状況をうまくモデル化できることを意味します。裾が非常に厚いため、平均や分散が無限になるような現象に対して頑健な分布です。
用途
ロバスト推定:
コーシー分布は、外れ値の影響が極めて強いデータに対して、ロバストな推定を行うために使われます。正規分布に比べて、コーシー分布は外れ値の影響を軽減するため、外れ値が大量に存在する場合には非常に効果的です。
外れ値が多いデータセットで回帰モデルを構築する際、損失関数にコーシー分布を用いると、外れ値に対してロバストな推定が得られます。
ベイズ推定における事前分布:
コーシー分布はベイズ統計における事前分布としても使われます。特に、非常に柔軟な事前分布が必要な場合や、外れ値に頑健なモデリングを行いたい場合に選択されます。具体的には、ロバストな線形回帰やパラメータの推定に役立ちます。
極端な値を扱う場合:
コーシー分布は、極端なデータや外れ値が重要な役割を果たすシステムにおいて有用です。経済データや金融市場データなど、外れ値が頻繁に発生する状況で、コーシー分布は適切な分布とされることがあります。
まとめ
ラプラス分布は、スパース性やL1正則化、外れ値の影響が少ない場合に適しており、主にLasso回帰や疎なデータを扱う機械学習アルゴリズムで使用されます。
コーシー分布は、外れ値が頻繁に発生するデータに適しており、ロバストな推定や外れ値が重要な要素となるモデルで使用されます。また、外れ値が多い場合のベイズ推定の事前分布としても使用されます。
それぞれの分布は、データの性質やタスクに応じて使い分けられ、ロバスト性や正則化を強化するために活用されます。
要するに絶対抑えておかないといけないポイントは…
ベイズ推定では①関心範囲を絞り込む場合、②関心範囲を拡大する場合、③それまでの外れ値(泡沫事象)が中央値になるなどして、関心空間が総入れ替えになる場合にベイズ更新が発生するが、「物語「シンデレラ」における「ガラスの靴の美女の登場」や「iPhone登場」の様な突発事象に該当する③そのものについて統計学的アプローチは無策に等しい。
その様な事象がどれだけ起こりやすいか(あるいは起こり難いか)によって、最適とされる確率分布予測も変わってくる。ラプラス分布はその様な事象が正規分布より有意に発生し難いと考えられる場合、コーシー分布はその様な事象が正規分布より有意に発生しやすいと考えられる場合に選ばれる確率分布である。
ああ、正規分布が「分布の女王」の座を降りて主観分布(分布の分布)の一部に組み込まれてますね。そう「単位元1を定める」という事は、統計学的アプローチにおいては「(観測における)中央値と外れ値の関係を定める」という事なのでこういう展開となる訳です。
ラプラス変換への拡張
ラプラス分布を回路方程式などを解く為に拡張したのがラプラス変換(Laplace Transform)とラプラス逆変換(Laplace Inverse Transform)。実際にはt>0の場合しか扱わないので指数分布の拡張とも見て取れるわけですが、それはそれ。
ラプラス変換そのものの定義
$$
F(s)=\int_{0}^{\infty} f(t) e^{-st} dt
$$
ラプラス変換の記号
$$
F(s)=\mathcal{L}[f(t)]
$$
ラプラス逆変換の記号
$$
f(t)=\mathcal{L}^{-1}[F(s)]
$$
回路方程式は、電気回路の動作を数式で表現したもので、電圧、電流、抵抗、インダクタンス、キャパシタンスなどの関係を記述します。代表的な回路方程式にはキルヒホッフの法則やオームの法則があります。
キルヒホッフの電流則(KCL): 回路の各接点(ノード)における電流の総和はゼロです(流入する電流と流出する電流が等しい)。
キルヒホッフの電圧則(KVL): 回路の任意の閉ループにおける電圧の総和はゼロです。
これらの方程式は、電気回路の解析において重要です。複雑な回路の動作を理解し、設計や最適化を行う際に使用され、エレクトロニクスの基本となります。

ラプラス変換はこの図だと主に「過渡現象(回路のスイッチが入ってから(t=0)定常状態に入るまでの電気的変化)」の解析に使われる解析。
回路方程式を解く際にラプラス変換は、時間領域の微分方程式を複素数領域の代数方程式に変換するために役立ちます。具体的には、次のような利点があります。
微分方程式の簡略化: 回路方程式は、インダクタやキャパシタが含まれると微分方程式になりますが、ラプラス変換を使うと、微分を単純な代数式に変換できます。これにより、解くのが容易になります。
初期条件の処理: ラプラス変換は、初期条件を含めた解析がしやすく、回路の初期状態を考慮した計算が可能です。
周波数領域での解析: 時間領域の振る舞い(過渡応答)だけでなく、回路の周波数特性(定常応答)を解析することも簡単にできます。
これにより、複雑な回路の動作を効率的に解析・解決できるため、制御系やフィルタ回路などで広く使用されています。
そう「単位元1」のあり方の一つとして、この様に複雑な諸要素の相互関係が相応の時間をかけて安定状態に入るケースも想定されるという話。こんな具合に随分と話が込み入ってきたところで以下続報…
