
【分布意味論時代の歩き方5パス目】現代社会から遡る「数学中心歴史観」?
以下の投稿においては最小二乗法(OLS=Ordinary Least Squares)を「葬送のフリーレン」に登場する「人を殺す魔法(ゾルトラーク)」に擬えました。
最小二乗法は当初ラグランジュやガウスといった大数学者にしか発想しえない「天才の御技」としてこの世界に降誕した。何が画期的だったといって、この時代まで人類はそもそも「式の数が多過ぎる連立方程式(行列演算でいうところの非正方行列)」を近似的に解く」手段すら持ち合わせていなかったのである。
地球の大きさと最小2乗法「葬送のフリーレン」の世界においては、その後の技術革新によって「(天才魔族クヴァールのみが考案し得た)人を殺す魔法(ゾルトラーク)」は「(魔法使いなら誰もが脊髄反射レベルで使いこなす様になった)一般攻撃魔法」に姿を変えた。同様に、当初はあまりに難物だったが故に探索的技法を用いたアプローチすら存在したとされる最小二乗法も、行列演算の概念が整備される過程で「(数学初学者から教わる)非正方行列を一般化逆行列を用いて求める」イメージに組み込まれた。
「葬送のフリーレン」の世界では「人を殺す魔法(ゾルトラーク)」を「魔族を殺す魔法」に発展させる過程で再びフリーレンの天才性を必要としたとされる。しかしながら(統計学や機械学習理論への到達に至る)最小二乗法の発展過程において、再び「大数学者だけが備える天才的閃き」が必要とされる事はなかった。そもそも「大数学者」の概念そのものが程なく滅んでしまったからである。





オイラーやガウスの様な「伝統的インテリ/ブルジョワ/政治的エリート階層(すなわち王侯貴族や高位聖職者)のパトロネージュを受け、天体運動や自然現象の様な絶対不動の物理学的存在の観測結果から誤差を除くのが統計の主な役割だった時代の大数学者」が長寿のエルフや魔族に見えてくる魔法…いやむしろこうしたイメージの大源流は「文明世界崩壊後、吸血鬼一族が貴族として人間世界を分割統治する様になった」菊地秀行「吸血鬼ハンターD (Vampire Hunter D, 1983年~)」を偲ばせる重厚なゴシックホラー的世界観ともいえるかもしれない?
Definitely need that "Vampire Hunter D" type of slaying for this bumbling but dangerous enough "Drac"!! #Svengoolie pic.twitter.com/w5SqjOa6xl
— Damien StMorien (@MorienSt) March 24, 2024
Vampire Hunter D (2000) pic.twitter.com/MVCrwRYExs
— Retro Anime (@retro_twt) March 23, 2024
Vampire Hunter D: Bloodlust❤️ pic.twitter.com/9FN6baXBYX
— 𝒗𝒂𝒎𝒑𝒊𝒓𝒆𝒂𝒓𝒕𝒔🧛🏻♀️ (@vampirearts) March 16, 2024
Vampire Hunter D: Bloodlust - Madhouse - 2000pic.twitter.com/Z9NZcZvNG4
— Otaking 🇵🇸 (@TheOtaking) March 16, 2024
VAMPIRE HUNTER D (1985) pic.twitter.com/orynGkCf29
— 𝑳𝑰𝑽𝑰𝑵𝑮 𝑫𝑬𝑨𝑫 𝑮𝑰𝑹𝑳 🦇 (@screamnhorror) March 17, 2024
という様な考え方を思いついたのですが、そもそもこうした数学史の背景に以下の様な歴史展開を想定する事が可能かもしれません。
「数秘術師」や「魔術師」の時代(イタリア・ルネサンス期~近世)
主要な経済的基盤…伝統的インテリ/ブルジョワ/政治的エリート階層(すなわち王侯貴族や高位聖職者)や「信徒」のパトロネージュ。
主要な観察対象…むしろ神学の領域やギリシャ・ローマ時代の古典の記述からの玉石混同の援用などが中心課題で、そもそも「特定の観察対象に注目する」なる問題解決意識自体が普及していなかった。
「大数学者や大物理学者登場以前の時代」に話を遡ると数秘術や魔術の世界に足を踏み込む展開を迎えます。
イタリア・ルネサンス期に「数秘術師」タルターリヤ(1500年~1557年)から「強引に」聞きだした三次方程式の解法を「勝手に」発表したカルダノ(Girolamo Cardano 1501年~1576年)による「虚数概念の流出」。
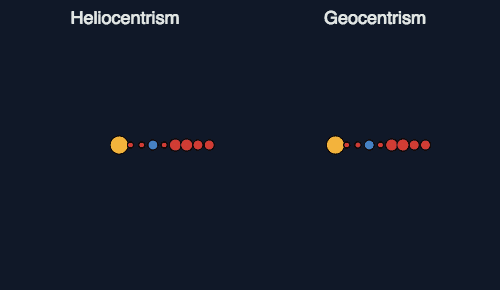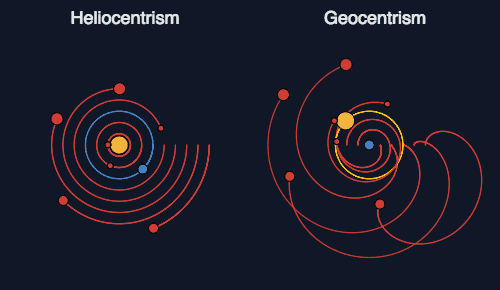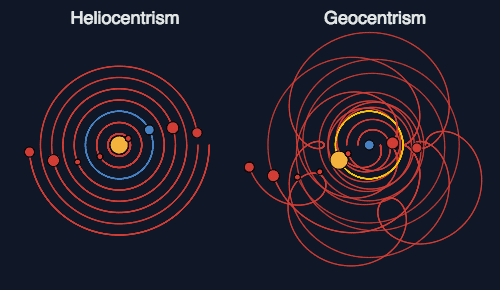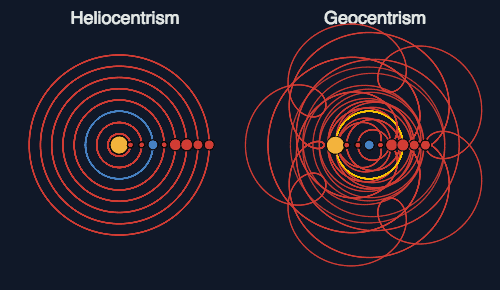
デンマーク貴族でもあった「魔術師」ティコ・ブラーエ(Tycho Brahe,1546年~1601年)から天体観測データを継承したドイツ人「天文学者」ヨハネス・ケプラー(Johannes Kepler,1571年~1630年)による「ケプラーの法則」の発表。ここで「(ティコ・ブラーエがその信念上認めたがらなかったといわれる)天体の軌道は概ね円軌道でなく楕円軌道である(より正確には「円錐曲線」である事を後にニュートンが証明)」なる科学的事実が数理的に示された事で天動説は致命的敗北を被る事となり「地動説の時代」さらには「観測の時代」が本格的に訪れる。
スコットランド貴族でもあった「魔術師」ジョン・ネイピア(John Napier, 1550年~1617年)とイングランド人「数学者」ヘンリー・ブリッグス(Henry Briggs, 1561年~1630年)の手になる「常用対数表」の発表。同時期にはそのコンセプトに基づいた対数尺も発明されて普及し「(面倒で時間の掛かる計算があらかじめ表にまとめられて出版される)科学諸表の時代」が本格的に始まる。なお余談ながらコンピューター開発は、この科学諸表を「より正確かつ短時間で得たい」なるモチベーションから出発。こういった展開全ての大源流に「計算器」ネイピアの骨(Napier's bones)概念がその始祖として君臨している訳である。
最初に構想された「プリンター」は、実際には印刷用の原版を作る機械であった。バベッジの意図としては、数表を出版する際に間違いやすい人手による植字という工程を経ずに大量に印刷したいという考えがあった。そのプリンターが紙にも結果を出力するようになっていたのは、階差機関の性能をチェックする手段という意味があった。

主に山本義隆「小数と対数の発見」辺りが扱ってる範囲の話ですね。
数学者クロネッカー(1823年~1891年)は「自然数を作り出したのは神で,その他はすべては人間の手の仕業だ」と述べたそうですが、実際に欧州で本格的に「貸方と借方の合計が0となる」複式簿記の概念が浸透するのはイタリアルネサンス期、当時先進地域だった地中海沿岸文化圏の算術を紹介するルカ・パチョーリ(1445年~1517年)の「スムマ(Summa de arithmetica, geometria, proportioni et proportionalita=算術、幾何、比および比例に関する全集,1494年1)がヴェネツィア共和国で出版されて以降。それ以前には、そもそも「ローマ数字で考えなければならない」制約のせいで「加法群=加法単位元0を中心として任意の数値に必ず合計すれば単位元0となる逆数が存在する等差数列(結合法則を満たす連続演算)」概念自体があまり広まっていなかった様です。この壁を越える為に、まずはアラビア数字と、(加方群概念そのものの具現化たる)複式簿記概念が広まり、「時間管理に周期性がある」期間会計概念に発展する必要があった訳です。
そう「(それまで地中海沿岸商圏におけるイスラム商人とヴェネツィア商人の間で秘伝とされてきた)貸方の総計と借方の総計が合致してなければならない複式簿記」の伝来こそが中世まで数学後進国だった欧州においては「反撃開始の狼煙」となったのです。
そもそも普及順序に注目するなら、複式簿記における「バランス概念」そのものが「偶力」や「作用・反作用の法則$${\vec{AB}=-\vec{BA}}$$(ニュートンの第3法則)」の大源流とも考えられたりする。

当時伝来した会計概念には複利計算法も含まれており、その延長線上において自然対数指数関数が発見され、遂には虚数概念や三角関数の概念を統合するオイラーの公式$${e^{θi}=cos(θ)+sin(θ)i}$$概念へと到達。
かかる欧州における「後発優位の法則」発動過程自体については…
強引に国体を郡県制に移行したフランス。しかしフランス革命からナポレオン戦争にかけての時代に国民の5人に1人を失い、かつ財源が枯渇したせいで産業革命導入は最初難航したのです(大英帝国一強時代の始まり)。
何しろ産業革命導入には社会インフラへの融資が欠かせないのに、当時のフランスには(身分制的見返りが期待出来る)国王や教会にし貸さない(フランス・ロスチャイルド家など)宮廷銀行家しか存在していなかったのです。
この逆境に挑んで見事「フランスの近代国家への脱皮」を成功いさせたのが「サン=シモン主義者」ルイ=ナポレオン大統領(後の皇帝ナポレオン三世)だったという次第。
皇帝ナポレオン三世は「脱皮=限界突破」の為に(それまで敵対してきた)マラーノ(ポルトガル系/ブラジル系ユダヤ人)や(絶対王政時代に追放した)ユグノーの産業資本家を誘致。(英国におけるナイチンゲールの活躍と前後して)統計学に基づく計画的都市再開発を遂行し、労働者向け団地を充実し、フランス産の砂糖大根をベルギーの精糖工場に運ぶ鉄道を完成させ、赤旗法(1865年-1896年)制定によって大英帝国の自動車産業が停滞した隙を突く破竹展開に最初の原動力を与えたのです。
そして、こうしてパッケージングされた「近代的工業国家への脱皮ノウハウ」を早速活用して「(経済学者アレクサンダー・ガーシェンクロンいうところの)後発性優位の法則」モデルケースに採用された「優等生国家」がドイツ帝国と大日本帝国二つだったという次第。
山本義隆「磁力と重力の発見」に詳細な記述がありますね。
文藝復興とも語られる14世紀から16世紀にかけてのルネサンスがヨーロッパ文化にもたらしたものは多方面に渡り、もちろん17世紀以降の近代科学を準備するものであった。しかしその道は錯綜し曲折している。私達の主題である磁力と重力の認識にかぎっていうなら、ルネサンスの功績はなんといっても魔術ーーなかんずく「自然魔術」ーーを復活させた事にある。実際力概念の発展とりわけ遠隔力の受容にとって、魔術の復活は単なる後退ではなく屈折して入るが基本的には前進であった。実際この時代、磁力は「隠れた力」の典型として、もっぱら魔術的・占星術的因果性を裏付けるものとして言挙げされていたのである。そんなわけで磁力は察し当たって自然魔術の研究対象であった。
ニュートンが天体間に働く重力を力学と天文学に導入して世界の体系を解き明かしたとき、今では考えられないくらい厳しい批判が、一方では新しい科学の提唱者であるデカルトのエピゴーネンやライプニッツから、他方では守旧派ともいうべきアリストテレス主義者から浴びせられたのである。ガリレイが潮汐にたいする月の影響という古くから経験的に知られてりた事実をかたくなに認めようとしなかったのも、まったく同じ理由からである。天体間の重力は魔術的・占星術的思考には馴染みよいものであったのにひきかえ、当時の新しい科学のリーダーにもあるいは旧来の科学の擁護者からも、認め難いものであった。
次に述べる「大数学者や大物理学者の時代」に入ってなお、こういう論争があったという話ですね。
魔術は中世キリスト教社会においては異端として抑圧され地上からは放逐されていたが、地下世界の潮流としてのみ存続してきた魔術が15世紀になって公然と地表に出現したのは、それだけキリスト教会のイデオロギー統制が緩んだ証左であろう。とりわけ教皇庁の置かれていたイタリアは群小国家に分断され、それらの小国家と教皇庁の間の領土と財産をめぐる世俗的な抗争はイタリア社会を長期に渡って荒廃・混乱させ、その間隙をぬって新興の都市市民ーー商人や職人や役人たちーーが確実に力を獲得してきていた。教皇庁の腐敗と堕落、そしてその支配体制の弱体化は、北ヨーロッパでは16世紀に宗教改革を生み出す事になったが、イタリアではそれに1世紀も先んじて人々をして現世的利益の追求へと向かわせる事になり、それがルネサンスの原動力となっていた。おのれを取り巻く社会が急激に変貌を遂げているのを見たイタリアの新興市民葬は、教皇庁を頂点とする教会の支配を支えているカトリシズムの救済信仰、現世厭離をうながす来世信仰になにがしか胡散臭いものを嗅ぎ取ったのである。
かつて東大闘争全学共闘会議の代表持つとめた「元運動家」の顔がギラリと垣間見えるのがたまりません。本格派左翼たるもの、かくあるべき…
初期ルネサンスの人文主義運動を哲学的な運動に転換させていった契機は、1438年・1439年にフェローラとフィレンツェで開かれた東西キリスト教会議と1453年のコンスタンティノープル陥落ーー東西ローマ帝国の滅亡ーーにともなって、古典文化をよりよく継承していたビザンチンの何人もの学者が数多くのギリシャ古典の写本を携えてイタリアに渡ってきたことだと言われている。こうして修辞学に偏していた初期人文主義とは肌合いの異なる思想的で学問的な運動が誕生した。そしてここにおいて、特にビザンチンの影響を受け神秘主義的な色合いを帯びた新プラトン主義そしてヘルメス思想が語られる様になったのであり、さらには異端の思想として遠ざけられていた魔術思想が公然と論じられる様になっていった。
とはいえ欧州における「魔術復活」は概ね(同じイタリア・ルネサンス期にパドヴァ大学やボローニャ大学の解剖学部で流行した)「科学実証主義概念の卵」としての新アリストテレス主義、すなわち
実践知識の累積は必ずといって良いほど認識領域のパラダイムシフトを引き起こすので、短期的には伝統的認識に立脚する信仰や道徳観と衝突を引き起こす。
逆を言えば実践知識の累積が引き起こすパラダイムシフトも、長期的には伝統的な信仰や道徳の世界が有する適応能力に吸収されていく。
なる考え方に併合され、次の「大数学者や大物理学者の時代」が膜を開ける展開を迎えるのでした。
「大数学者」や「大物理学者」の時代(大航海時代~1848年革命の頃)
主要な経済的基盤…伝統的インテリ/ブルジョワ/政治的エリート階層(すなわち王侯貴族や高位聖職者)のパトロネージュ。
主要な観察対象…天体運動や自然現象の様な「(時代性や地域性の影響を概ね受けない)唯一無二の絶対的存在」。それはまだまだ「神が創造したこの世界の神秘の確認作業」なる認識によって「神学の婢女(はしため)」とイメージされていた。
上掲の様な歴史的経緯から「大数学者」は物理学者を兼ねる事が多く、さらには物理学が「人類未到の数理領域へのインスピレーションの導き手」として機能する機会も多かった様です。
ここで興味深いのが微積分概念の発展史。
ニュートン卿(Sir Isaac Newton, 1642年~1727年)が微積分概念研究に取り組んだのはロンドンにペストが大流行して大学も閉鎖された1665年から1666年。この時期のニュートンは故郷のウールスソープへと疎開し、その直前に得た奨学金で暮らせた為、学問に専念する生活が送れた。一方、ライプニッツ(Gottfried Wilhelm Leibniz, 1646年~1716年)が微積分概念研究に取り組んだのはマインツ選帝侯の使者としてパリ滞在中に侯の死より失職した1673年からカレンベルク侯ヨハン・フリードリヒに顧問官兼図書館長として雇われハノーファーに移住した1676年にかけて。「世界の首都」パリで求職活動の傍らオランダ人数学者/物理学者クリスティアーン・ホイヘンス(Christiaan Huygens,1629年~1695年)らと交流し知的刺激を受けたのも大きいとされる。
「テイラー級数の考案者」ブルック・テイラー(Brook Taylor,1685年~1731年)こそ、その主張の韜晦さ故に時代の流れの中に埋もれてしまったが、同じ王立協会フェローながらスコットランド出身でニュートンの考えを明快に解説してスコットランド啓蒙運動に多くの影響を与えた「マクローリン級数の考案者」コリン・マクローリン(Colin Maclaurin,1698年~1746年)や非国教派牧師を本業に選んだ「ベイズの定理の考案者」トーマス・ベイズ(Thomas Bayes ,1701年~1761年)の名前は後世に伝わった(ただし「ベイズの復権」は比較的最近になってから)。
全体として「絶対王政時代の宮仕え」の窮屈さと、それから離れる形でしか得られなかった解放感について思いを馳せざるを得ない。しかしその一方で「国体維持に十分な火力と機動力を備えた常備軍を中央集権的官僚制の徴税によって賄う主権国家体勢」滋養目的で英国における王立協会フェロー(Fellowship of the Royal Society)、フランスにおける科学アカデミー(Académie des sciences)やエコール・ポリテクニーク(École polytechnique,通称X)といった制度が整備されたのもまたこの時代だったのです。
しかしながら、結論からいうとこの時代まで遡る産業角形黎明期、「海賊でも(カリブ海沿岸や南アフリカの)奴隷制農場主でも国家の富強に貢献すれば貴族になれた」大英帝国ほどには新興富裕階層に階級流動性を用意出来なかったフランスにおいてはフランス革命(1789年~1799年)が勃発して「大英帝国一強時代」が到来してしまうのでした。
しかしまさに、かかる事情による「二流後進国への転落」が、上掲の形でのフランスにおける「後発優位の法則」発動に繋がり、そのおこぼれに「三流後進国」ドイツ帝国や大日本帝国が与る訳ですから「人間万事塞翁之馬」としかいいようがありません。
そしてまさにこのフランス革命こそがメートル法制定を契機としての最小二乗法登場の契機となった訳ですが、この時期に複素平面概念が普及したのは果たして偶然なのでしょうか?
地球の大きさと最小2乗法
当時をフランス側の立場で経験したのはラプラス(Pierre-Simon Laplace, 1749年~1827年3月5日)はとラグランジュ(Joseph-Louis Lagrange, 1736年~1813年)。不思議とこの二人は複素平面の概念と結びつけて語られる事がない。ラプラスはベイズ推定だけでなくラプラス変換の考案者でもある筈なのに不思議な話ではある(そういえば確かにラプラス変換の式は「見掛け上」虚数記号を含まない)。
$$
F(s)=\int_{0}^{\infty} f(t) e^{-st} dt
$$
これはもしかしたら「直交座標系(Cartesian coordinate system)の考案者」デカルト(René Descartes, 1596年~1650年)の虚数蔑視感情がフランス数学の伝統に継承された結果かもしれない。いずれにせよ複素平面概念登場以前の直交座標系は回転や2次元以上の座標軸を扱う事が出来なかったのである。少なくとも表面上は。
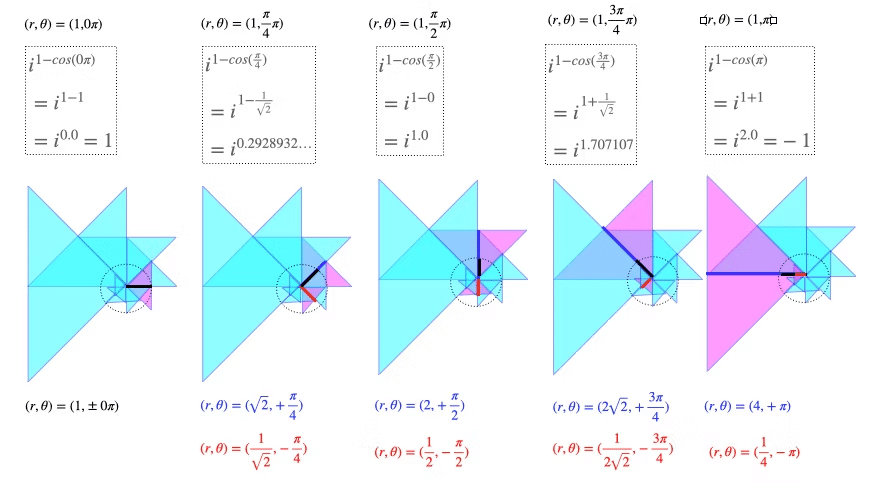
最小二乗法を最初に考案したのがラグランジュかドイツ人数学者ガウス(Johann Carl Friedrich Gauß/Carolus Fridericus Gauss, 1777年~1855年)かはともかく、ガウスが最小二乗法の最大の弱点たる外れ値除去の為に誤差関数を考案してその精度を高めた事実は動かない。また複素平面概念の考案者とも限らないが、巡回群の概念を追加してその使い勝手を飛躍的に向上させた事実もまた動かない。出自こそ平凡だがブラウンシュヴァイク侯爵から厚遇され生涯金に不自由する事がなかったばかりか投機活動でそれなりの蓄財もしていた様である。「数学は生計を立てる手段になり得ない」と考え1807年にゲッティンゲンの天文台長に就任。
当時はまだ複素数が完全なる市民権を得ておらず、できれば使用を避けたいという風潮のあった時代であった。そのため、ガウスは代数学の基本定理を証明した学位論文では誤解を避けるために虚数を表に出さず、多項式が実数の範囲内で1次または2次の因数に分解されるとした。そのような時代にあっても、早くから虚数への偏見から完全に自由であったガウスは複素数の世界に深く分け入り、数多の美しい結果を得た。
ガウスは、そうした成果の全てを発表しなかったが、彼がそのように、自身の成果を発表せずにいたのにはいくつかの要因があると思われる。
①ガウスにとっては研究で美しい結果を得ることが最大の報酬であり、他人の認知を必要としなかった。
②世間の無理解、誤解によって生ずる論争の煩わしさを嫌った。実際、ガウスは非ユークリッド幾何学の可能性についての自身の考えが世に漏れることに極めて慎重であった。
③当時の成果発表手段の乏しさ。その頃は今のように論文原稿を送るべき学会誌や論文雑誌は存在せず、成果発表は主として自家印刷の小冊子や単行本によった(しばらくして学士院や大学の紀要も)。実際、ガウスの整数論は単行本として発表された。そしてアーベルの「代数方程式に関する論(五次の一般的な方程式を解くことの不可能の証明)」は自家印刷の粗末な小冊子として出されて、その時は世間に認知されずに終わった。アーベルのこの論文や楕円関数論が世間に認知されたのは1826年に論文雑誌「クレレ誌」が創刊され、それに寄稿しての話である。このような時代にあってガウスは解析学の大著述を計画するが、研究が進展して考察の範囲がとめどもなく拡大していき完結の機会を逸し、また測量学の実地での測量や膨大な数値計算、天文観測などで多忙であったこと、ナポレオンによるヨーロッパの政治混乱による経済的困窮などにより、ついに世に出ることがなかったという。
そう「大数学者/大物理学者の時代」とは「誰もが愛(i)についてそれなりに熟知品がら、可能な限りそれを語ろうとしなかった」ムッツリスケベの時代でもあったのです。この辺りも「葬送のフリーレン」の世界観におけるエルフや魔族の在り方と重なってくるところがあるという…




その一方で「大数学者の時代」には、その末期にガウスがノルウェー人数学者アーベル(Niels Henrik Abel 1802年~1829年)を、フランス人数学者コーシー(Augustin Louis Cauchy, 1789年~1857年)がガロア(Évariste Galois, 1811年~1832年)を冷遇して早逝させた黒歴史もあったりします。
なのでてっきり「アフィン(affine)変換」のアフィン(Affine)さんもそうした冷飯組の一人かと思い込んでいた時期があるのですが、実は違っててラテン語で「類似・関連」を意味するaffinis由来との事。
超基本の行列計算…アフィン変換
$$
\begin{pmatrix}
X_1 \\
Y_1 \\
1\\
\end{pmatrix}=
\begin{pmatrix}
a & b & e\\
c & d & f \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
$$
並行移動(T_x,T_y)
\begin{pmatrix}
X_1\\
Y_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & T_x \\
0 & 1 & T_y \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
$$
拡大縮小(S_x,S_y)
\begin{pmatrix}
X_1\\
Y_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
S_x & 0 & 0\\
0 & S_y & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
$$
回転(θ)
\begin{pmatrix}
X_1\\
Y_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
cos(θ) & -sin(θ) & 0 \\
sin(θ) & cos(θ) & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
$$
剪断(θ)
\begin{pmatrix}
X_1\\
Y_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0 \\
tan(θ) & 1 & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
この様にアフィン変換では「同次座標系における行列演算」によって虚数概念を用いる事なく回転をこなします。おや?虚数軸は何処に?実は「同次座標系における行列演算」は平面(x軸,y軸)に対してしか作用しないのがミソで、その時使われてないz軸に割り振られているのです(要するにこれが、多くの人間が「何の為にあるか」説明出来ない「3列目/3行目」の正体?)。鏡像変換行列について考えてみれば分かりますよね。
$$
\begin{pmatrix}
x' \\
y' \\
\end{pmatrix}=
\begin{pmatrix}
\mp i^{1-cos(θ)} & 0 \\
0 & \pm i^{1-cos(θ)} \\
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
\end{pmatrix}
$$
$$
\begin{pmatrix}
-i^{1-cos(0)} & 0 \\
0 & +i^{1-cos(0)} \\
\end{pmatrix}=
鏡像変換行列\begin{pmatrix}
-1 & 0 \\
0 & 1 \\
\end{pmatrix}
$$
$$
\begin{pmatrix}
-i^{1-cos(\pm \frac{π}{2})} & 0 \\
0 & +i^{1-cos(\pm \frac{π}{2})} \\
\end{pmatrix}=\begin{pmatrix}
\mp i & 0 \\
0 & \pm i \\
\end{pmatrix}
$$
$$
\begin{pmatrix}
-i^{1-cos(\pm π)} & 0 \\
0 & +i^{1-cos(\pm π)} \\
\end{pmatrix}=\begin{pmatrix}
1 & 0 \\
0 & -1 \\
\end{pmatrix}=-
\begin{pmatrix}
-1 & 0 \\
0 & 1 \\
\end{pmatrix}
$$
こんな演算見た事ありません。虚数はあくまで原則としては「(交流電気の様に原則として1次元上を伝導する電流の流れを2次元的に把握するケースの様に)新たに次元を増やす意味がない時、増やすとかえって面倒が増える場合」に用いられる実数代替表現に過ぎません。そしてこういう場合には黙って三次元座標系に切り替え、演算ごとに「無視する軸」を切り替えていくだけで事足りるので愛(i)の出番がない訳です。何たる愛(i)に対する鉄壁ガード…
$$
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
a & b & c & j\\
d & e & f & k\\
g & h & i & l \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
並行移動(T_x,T_y,T_z)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0 & T_x\\
0 & 1 & 0 & T_y\\
0 & 0 & 1 & T_z \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
拡大縮小(S_x,S_y,S_z)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
S_x & 0 & 0 & 0\\
0 & S_y & 0 & 0\\
0 & 0 & S_z & 0 \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
x軸まわりの回転(θ)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & cos(θ) & -sin(θ) & 0\\
0 & sin(θ) & cos(θ) & 0 \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
y軸まわりの回転(θ)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
cos(θ) & 0 & sin(θ) & 0\\
0 & 1 & 0 & 0\\
-sin(θ) & 0& cos(θ) & 0 \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
Z軸まわりの回転(θ)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
cos(θ) & -sin(θ) & 0 & 0\\
sin(θ) & cos(θ) & 0 & 0 \\
0 & 0 & 1 & 0\\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
確かに上掲の二次元座標系上における水平操作が三次元座標系における「Z軸を固定しての回転」に対応してるのが分かりますね。なお鏡像回転は「X軸を固定しての回転」と「Y軸を固定しての回転」の合算として計算しますが、そのままだと2θ回ってしまうので$${\frac{θ}{2}}$$ずつ回す事になります。
この様に、特に回転操作について「演算を刻む(水平操作に分解して合算する)」必要があるのがアフィン変換の不便なところで、近年「ハミルトンの四元数」が宇宙船やドローンの制御だけでなくゲームプログラミングの世界でも復権を果たしたのにはこの辺りに理由がある様です。ただし、やはり「フルスペック四元数」再評価ではない模様(式に$${\frac{θ}{2}}$$が登場する理由は鏡像反転の場合と同じ)…
まず抑えておきたいのは、クォータニオンは回転のために存在する概念ではないということだ。複素平面の3次元拡張として生まれたものであり、それがたまたま回転表現に便利だった、ということ。実際、回転のために使用されるクォータニオンは単位クォータニオンであり、直交変換に特化した特別なクォータニオンだ。
くどいようだけど、回転じゃないクォータニオンが普通なのであって、それを回転に使用するように特化しちゃおう、ということ。たいていの人にとって、普段計算機で使っているクォータニオンは回転に特化されているはずだ。(例えば効率のために計算アルゴリズムが簡略化されている)
$$
A=(n_xsin(\frac{θ}{2}),n_ysin(\frac{θ}{2}),n_xsin(\frac{θ}{2}),cos(\frac{θ}{2}))
$$
こういう「便利だから部分導入」アプローチは∇演算による勾配(∇f=grad f:四元数の傾き)、発散(∇・A=div A:四元数の内積部)、回転(∇xA=rot A:四元数の外積部)を求める計算にも出てきます。
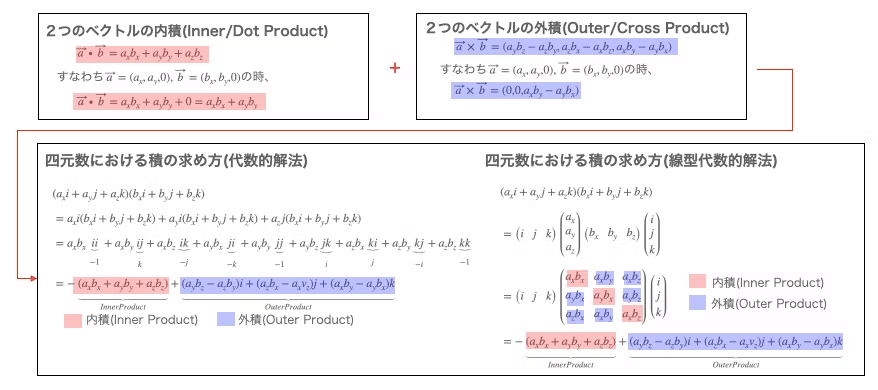
①まずはナブラ演算を$${∇ \equiv i\frac{∂}{∂_x}+j\frac{∂}{∂_y}+k\frac{∂}{∂_z}}$$あるいは$${ ∂_x=\frac{∂}{∂_x},∂_y=\frac{∂}{∂_y},∂_z=\frac{∂}{∂_z}}$$と置いて$${∇ \equiv i∂_x+j∂_y+k∂_z}$$と定義する。
②任意の空間座標r=(x,y,z)の関数Xの値域X(r)として定まる量を場(field)という。この時(スカラー量が空間座標rの関数として与えられる)スカラー場ψ(r)にナブラ演算子∇を作用させた結果としての(ベクトル量が空間座標rの関数として与えられる)ベクトル場α(r)=勾配(gradient)$${∇ψ=i∂_xψ+j∂_yψ+k∂_zψ=i\frac{∂ψ}{∂_x}+j\frac{∂ψ}{∂_y}+k\frac{∂ψ}{∂_z}}$$
③ベクトル場α(r)に「内積の様に」作用させた結果としてのスカラー場ψ(r)=発散(devergence)$${∇・α=∂_xα_x+∂_yα_y+∂_zα_z=\frac{∂α_x}{∂_x}+\frac{∂α_y}{∂_y}+\frac{∂α_z}{∂_z}}$$
④ベクトル場α(r)に「外積の様に」作用させた結果としてのベクトル場α(r)=回転(rotation)$${∇×α=i(∂_yα_z-∂_zα_y)+j(∂_zα_x-∂_xα_z)+k(∂_xα_y-∂_yα_x)=i(\frac{∂}{∂_y}α_z-\frac{∂}{∂_z}α_y)+j(\frac{∂}{∂_z}α_x-\frac{∂}{∂_x}α_z)+k(\frac{∂}{∂_x}α_y-\frac{∂}{∂_y}α_x)}$$
⑤ちなみにスカラー場ψ(r)の勾配(grad.)∇ψの回転(rot.)∇×(∇ψ)=0(無次元量だからベクトル成分を持たない)、ベクトル場α(r)の回転(rot.)∇×αの発散∇・(∇×α)=0(互いに直交してるから内積0)、スカラー場ψ(r)の勾配(grad.)∇ψの発散(dev.)∇・(∇ψ)はラプラス演算子(ラプラシアン)$${∇^2 \equiv ∇・∇=(\frac{∂^2}{∂_x^2}+\frac{∂^2}{∂_y^2}+\frac{∂^2}{∂_z^2})}$$を用いて$${∇^2ψ}$$、ベクトル場α(r)の回転∇×αの回転$${∇×(∇×α)=∇(∇・α)- ∇^2α}$$、そしてラプラシアンはスカラー微分演算子なのでこれをベクトル場α(r)に作用させると成分それぞれに働いて$${∇^2α=i(∇^2α_x)+j(∇^2α_y)+k(∇^2α_z)}$$となる。もはや数学というより物理演算の世界?
こういう難しい考え方を学ぶ過程は、知識獲得そのものへのモチベーションに加え「未知の事象へのアプローチ手段の確立(全くの素人がその筋のそれなりのエキスパートに成長する過程の可能な限りにおける一般化)」なる知的興奮が伴うのが素晴らしい。
ゲームプログラマのための数学の歩き方 - ラプラシアン編本来の演算が難し過ぎるからカプセル化してメソッドのパラメーターによって欲しい値を取り出す」という発想は、まさしくオブジェクト指向プログラミングにおけるポリモーフィズム(polymorphism=多態性)概念そのもの。
全部四元数普及の為にハミルトンが必死で最初の基礎を整えたといってよい。物理学者でもあったハミルトンは、ある意味「最後の大数学者」の風格を備えているとも?
この辺りの話も、それぞれの大数学者/大物理学者の皆さんが何処まで到達していたか知り様がないのが「ムッツリスケベの時代」の「ムッツリスケベの時代」たる所以という…
「統計学者」と母集団推定の時代(産業革命時代~現代)
主要な経済基盤…「国家(すなわち国体維持に十分な火力と機動力を備えた常備軍を中央集権的官僚制の徴税によって賄う主権国家体勢)」およびその協調体勢。全世界に張り巡らされた機関車と汽船の交通網と生産機械化に伴う大量生産/大量消費システムに支えられた企業群。すなわち産業革命浸透に伴って全面化した資本主義システムそのものからの依頼。
主要な観察対象…上掲の資本主義システムが事業の計画的遂行の為に統計データを必要とするあらゆる集団(菌類から人間や動物の「社会」まで)。大量生産/大量消費システム成立の余波で消費の主体が伝統的インテリ/ブルジョワ/政治的エリート階層(すなわち王侯貴族や高位聖職者)から新興ブルジョワ階層や庶民に推移したので、これも観測対象に加えねばならな君なった。
上掲の様な「奥ゆかしい」古き良き時代を終わらせたのが軍隊近代化、都市計画の実施、全世界に張り巡らされた機関車と汽船の交通網、生産機械化に伴う大量生産/大量消費スタイルといった「資本主義システムの到来」なる喧騒だったのです。
もはや「(愛(i)について知らないフリを通すのが奥ゆかしいとされる)ムッツリスケベの時代」の流儀は通りません。とはいえ…
まず先陣を切ったのはアイルランド人数学者ハミルトン(William Rowan Hamilton, 1805年~1865年)による「ハミルトンの四元数」の発見(1843年)。ただし時代が早過ぎたのとその内容があまりに難解だった事が重なってすぐに普及した訳ではなかったのである。
晩年のハミルトンは、アルコール中毒に溺れながら誰にも理解されることのない数学研究に没頭し、暴飲暴食による痛風に苦しんだ末に1865年にダブリンの自宅で息を引き取った。遺体が発見された時、ハミルトンの部屋は酒と肉汁にまみれた二百数十冊のノートで埋め尽くされており、この中には正しいもの、誤ったもの、判断のつかないものが入り混じった数式の山が残されていたという。また四元数は一部に「四元数カルト」と呼ぶべき一団を構成するものの、大勢からは無視され、省みられるまでに100年ほどの時間を必要とした。
確かに「ハミルトンの四元数」は全体像こそ難解だが部分単位で導入した際の有用性は高かった。このアプローチで大成功を収めたのが電磁気学の世界に複素数概念を持ち込み、ラプラス変換を再評価した「英国の叩き上げ技師」ヘヴィサイド(Oliver Heaviside, 1850年~1925年)や、統計力学の成立に貢献した米国人数学者ギブズ(Josiah Willard Gibbs, 1839年~1903年)らで、その結果普及したのが「ハミルトンの四元数」から「内積」や「外積」の概念を部分援用したベクトル解析概念だったという次第。
ハミルトンの四元数は、彼が1843年に提案した数学的概念であり、ベクトルや行列のような概念を含んでいます。しかし、四元数はその複雑さや理解の難しさから、一般的な科学技術の応用である電磁気学や力学などの分野での普及が限られていました。
一方で、ヘヴィサイドやギブスが提案したベクトル概念は、その後の科学技術の進歩に合わせて、特にベクトル解析が自然な形で適用できる電磁気学や力学などの分野で広く受け入れられました。ベクトル概念は幾何学的にも直感的であり、計算上も直感的であるため、多くの科学者や技術者にとって使いやすかったからです。
また、ベクトル概念は行列やテンソルなどの他の数学的概念とも密接に関連しており、これらの概念と組み合わせることで、さらに多くの問題に対処できる柔軟性を持っていました。
そのため、ヘヴィサイドやギブスのベクトル概念は、四元数よりも科学技術の応用で広く採用され、普及したのです。
上掲のアフィン変換(同次座標系における行列演算)と同じく「隠し味に使う程度なら問題ない」発想。とどのつまり「ハミルトンの四元数」が扱う数理は重力の掛かる方向が定まってない無重力下でこそフルスペックが必要とされる内容で、だから、こそ宇宙船やドローンの制御用力学として復権を果たす訳ですが、重力に拘束された地球の表面上に生まれ「カンブリア爆発期に授かった視覚と視覚情報を処理する脊髄の末裔」で考える人類にはオーバースペックとなる様なんです? その一方で「(虚数を1個しか使わない)複素数概念」は新興技術たる電磁気学の世界にガッツリと組み込まれる展開を迎えたのです。
電気工学の世界に最初に愛(i)の概念を伝導したのが「アカデミズム的教養とは縁もゆかりもない叩き上げエンジニア」ヘヴィサイド(Oliver Heaviside, 1850年~1925年)で「消化の原理を知らなくたって飯は食うだろ?」なる名言を後世に残しました。
機械学習系の人は「ヘヴィサイドの階段関数の考案者」として記憶に留めているかもしれません。
「そんな骨董品級の概念なんてもう忘れたね!!」とおっしゃる方もいらっしゃるかもしれませんが、あの波形案外合成が難しい上…
最近は活性化関数界隈におけるランプ関数の再評価なんて流れもあるのでなかなか侮れなかったりするのです。

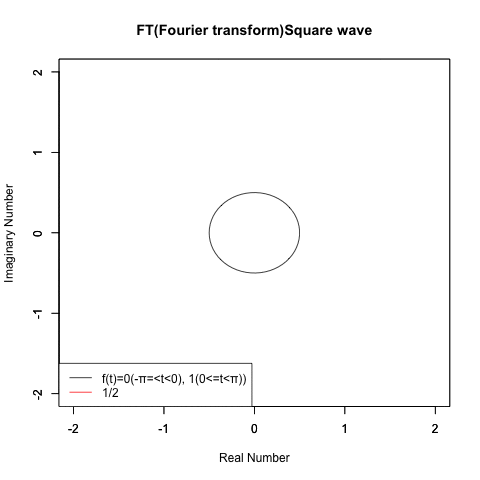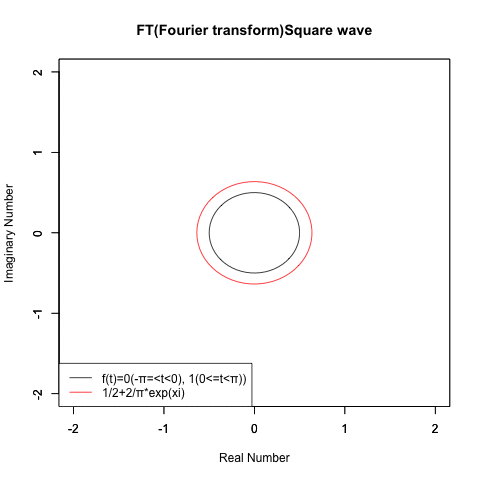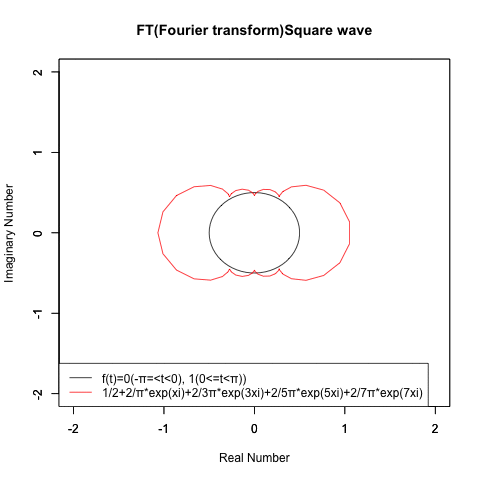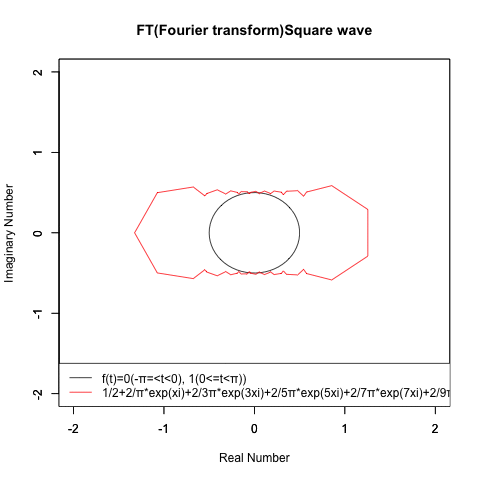





その一方でガウスが天体観測などの誤差を最小限に留める為に考案した誤差関数は「サンプル数を無限に大きくしていけば多くの分布が最終的に到達する母集団分布」と考えられる様になり、その分布との偏差を「平均」と「分散」の2パラメーターで調整する「正規分布」概念が普及したのもこの時代の特徴といえましょう。
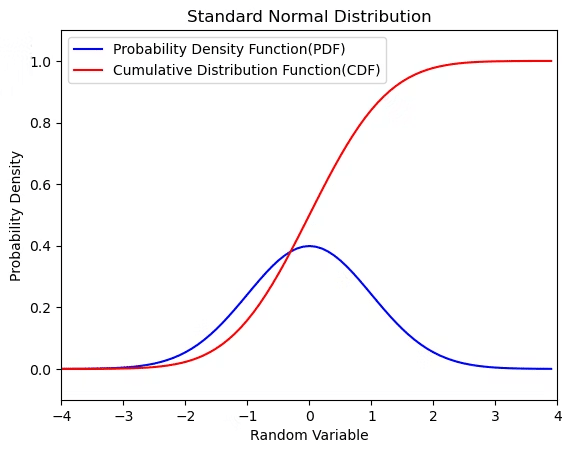
中央極限定理の研究自体は「大数学者/大物理学者の時代」まで遡るが、当時はまだまだ「この世界の様々な事象には、神があらかじめ定めた固有の出現確率が存在する」という信念が根強く存在したので大数学者や大物理学者は声を大にしてそれを主張しては来なかったのだった。また、議論対象が天体や自然現象である限りそうした「信念の強い人々」の日常的不安を煽る心配もなく、それでなんとか両者の間にはなんとかギリギリで平和が保たれてきたといえよう。
資本主義の時代に入り、物事を計画的に進める為にあらゆる展開についての予測データが必要となるとそうもいってられなくなった。
工学部の学生さんでも、このぐらいの認識だったりする
— macro-k@品質工学 (@macrok4) April 7, 2024
いや、設計者でもこういう感じの人、たまにいるな… pic.twitter.com/yKIwsoxwqv
最初にこの問題に足を踏み込んだのばフランシス・ゴルトン(Sir Francis Galton、1822年~1911年)で、当時議論が沸騰していた「天才や犯罪者の出現は遺伝要因か環境要因か」なる問題についての数理的アプローチを試み「優生学」なる思わぬ落とし子を残してしまった事で知られる。その後の統計学の発展過程で彼の立脚した仮説のほとんどは棄却されてしまったものの「誤差関数の累積度数分布$${\frac{1}{π} e^{-x^2}}$$」を「ガウス分布」と呼び「多くの自然現象に見られる分布で、それらはサンプル数を無限大に増やし続ければこれに回帰する」と考えた事は「統計学者/優生学者」ピアソン(Karl Pearson, 1857年~1936年)やフィッシャー(Sir Ronald Aylmer Fisher, 1890年~1962年)のパラメトリック統計学に継承され、歴史に不可逆的に刻まれる事になったのである。実際、現場の多くでその考え方は有用だったので、気付くと「この世界の様々な事象には、神があらかじめ定めた固有の出現確率が存在する」と考える伝統はほぼ一掃されていたという次第。
観測対象が天体運動や自然現象の様な「(時代性や地域性の影響を概ね受けない)唯一無二の絶対的存在」でなくなり、多種多様な予測ニーズに応えなければならなくなった事から新たな統計技法が次々と生み出された。集団間の平均値の差異が有意味かどうか検定するt検定や分散分析(ANOVA=ANalysis OF VArianc)、潜在因子の直交座標系を構築する因子分析(Factor Analysis)、観測データの次元削減を試みる主成分分析(PCA=Principal Component Analysis)…
実は展開開始時期が若干遅れるだけで、主要経済基盤も分析技法も次に述べる「機械学習と意味分布論の時代」とほとんど連続していたりします。最大の違いは観察対象で、ここに述べた「統計学者と母集団推定の時代」のそれは、細菌にしろ生物や人間の集団にせよ機械類にせよ何らかの形で物理的実体を備え、その事が不確定要素の源泉となっている場合が多いのです。ところが「機械学習と意味分布論の時代」の主要観測対象は「情報そのもの」となります。どうしてそんなジャンルが成立して21世紀に大きな意味を持つ事になったのか?まずはそこから始めないといけません。
機械学習と意味分布論の時代(第二次世界大戦期~現在)
主要経済基盤…「統計学者と母集団推定の時代」同様「資本主義システムそのもの」
主要観測対象…データそのもの
まず最初に注意しないといけないのが「用語の言い換え」です。
最小二乗法などによる分類や回帰…「教師あり学習」
(平均や回帰式の値域を基準とする)残差…損失
なお機械学習理論は決定木概念導入以降「順位付けも分類付けも一括して扱うアルゴリズム」を獲得しているので、その時点で既存の統計尺度概念を超越した存在に変貌していたりします。
決定木アルゴリズムは、機械学習やデータマイニングの分野で広く使用される重要な手法です。以下に、決定木アルゴリズムの歴史を要約します。
1950年代: 決定木アルゴリズムの初期の形態は、情報理論の概念に基づいています。これは、クロード・シャノンによって提案された情報理論の基礎を利用したものでした。この時期には、機械学習やパターン認識の分野がまだ発展途上であり、決定木はそのような手法の一部として着目されていました。
1960年代〜1970年代: 決定木アルゴリズムは、統計学やパターン認識の分野で発展し始めました。特に、モチーフ解析や分類問題などの問題に対して、決定木が利用されるようになりました。
1980年代〜1990年代: 決定木アルゴリズムの一般的な応用が増え、さまざまな変種や派生が提案されました。この時期には、ID3(Iterative Dichotomiser 3)やCART(Classification and Regression Trees)などの代表的な決定木アルゴリズムが開発されました。
2000年代〜現在: 決定木アルゴリズムは、機械学習やデータマイニングの分野でますます広く使用されるようになりました。特に、決定木は直感的で解釈しやすいことから、ビジネスや産業界でも広く受け入れられています。また、ランダムフォレストや勾配ブースティングなどのアンサンブル学習手法が開発され、決定木の性能や汎化能力を向上させるために利用されています。
総じて言えば、決定木アルゴリズムはその直感的な性質と優れた解釈性から、機械学習の初心者から専門家まで幅広いユーザーに利用され、進化してきました。
ちなみに「いかにも優等生の模範解答らしい」ChatGPTの説明から抜け落ちてしまった「最も重要なパラダイムシフト」が以下。
1990年代に入ると、CART(Classification and Regression Trees)アルゴリズムが登場しました。CARTアルゴリズムは、ジニ不純度という指標を用いて分岐条件を決定し、分類性能をさらに向上させることが可能になりました。また、CARTアルゴリズムは分類だけでなく回帰にも適用可能であることから、決定木アルゴリズムの応用範囲が広がりました。
そう、このCART登場以降、既存の統計学尺度は大幅な概念修正を余儀なくされる展開を迎えたのだった(より具体的には、名義尺度と順序尺度の間への分類尺度の追加と、その分類尺度と順序尺度の境界線の曖昧化)。
それにつけても、一体いつから始まった言い換えなのでしょう。いずれにせよ1958年にデイヴィッド・コックスがロジスティック回帰の概念を発表して、同意時期単細胞パーセプトロンの概念が樹立するまでは存在しなかった考え方である事実は動きません。なおChatGPTに「ロジスティック回帰はお前の先祖か?」と尋ねたら「あんな単細胞生物が私の先祖の筈がない」という答えが返ってきました。
「(最小二乗法など既存の方法を用いた)既存データからの回帰式算出」を「教師あり学習」と言い換えたロジスティック回帰や単純パーセプトロンのインパクトはよほど大きかったらしく、ノーバート・ウィーナー「サイバネティクス」の論調が(それ以前に執筆された)1948年初版箇所(1章~8章)と(それ以降に執筆された)1961年増補箇所(9章と10章)では大幅に変わっているほど。ただし「主要観測対象をデータそのものとする」方針自体はそれ以前から、というより最初からの前提だったのです。
第二次世界大戦の初期におけるドイツ空軍の優勢と、イギリスの守勢とから、多くの科学者が高射砲の性能向上を図ろうとしていた。戦争前でさえも航空機の高速化が、従来の対空火器照準方法を全く時代遅れのものとしてしまい、火器の制御装置の内部に必要な計算機構の一切を組み込む必要のある事はことがはっきりとわかっていた。しかし、それは極めて困難な事であった。今まで扱ってきた標的と違って、飛行機の速度がそれを撃ち落とそうとする砲弾の速度にだいぶ近くなってきたからである。したがって標的に狙いを定めて砲弾を発射するというのではなく、砲弾と標的とがある時間後の空中でぶつかる様に発射する必要がある。そこで飛行機の未来の位置を予測しなければならない事になった。
非常に物騒な話ですが、まさにこの「標的を真芯で捉える」という血生臭い問題意識こそが情報理論の出発点となったのです。
非常に物騒な話ですが、まさにこの血生臭い問題意識こそが情報理論の出発点となったのです。
非常に多くの現象において、われわれは時系列(time series)、すなわち時間の経過に応じて分布している数量、あるいは数量の系列を観測する。自記温度計で記録される温度とか、毎日の株式取引における株の相場(終値)とか、気象台から毎日発表される気象情報とかは、みな連続的な、あるいは離散的な、単独あるいは多重の時系列である。これらの時系列は比較的緩やかに変動するから、筆算や計算尺または卓上計算機の様な、普通の数値計算機よって処理するのに適している。これらの研究はすでに統計理論の伝統的な部分に属している。
一般にはあまり認識されていないことではあるが、電話線・テレビジョン回路、レーダー装置のある部分などの様に急速な変化を示す電圧の系列も上述のものと同様に統計学や時系列論に属するものである。ただしそれらを結合・変換する装置には、高速な動きをすることと、入力の極めて急激な変化と同一歩調で結果を出す事が要求される。これらの装置、すなわち電話の受話器、濾波器、ベル電話研究所のヴォコーダー(vocorder)の様な自動的音声符号化装置・周波数変調回路とそれを使ったは全て本質的に高速どの演算装置であり、その働きは統計学研究所の計算機械類・予定表・計算手などの全体に匹敵するものである。これらの装置のなかには対空火器制御系の自動測距機や自動照準器と同様に、それらを使うのに必要な精緻な工夫が前もって組み込まれている。それらのものを組み入れておかねばならない理由も対空火器の場合と同様である。すなわち、どちらの場合も動作の連鎖は非常に早いものでなければならないから、人間がその一部として介入する事は許されないのである。
この考え方から出発したから情報量の定義はこうなった訳です。
$$
事象Eが起こったことを知らされたとき受け取る自己情報量I(E)=log\frac{1}{P(E)}=-logP(E)(ただしP(E)は事象Eが起こる確率)
$$
例えば、52枚のトランプから無作為に1枚を取り出すという試行を考える。「取り出したカードはハートの4である」という事象の情報量は、前述の定義から log 52 であると分かる。ここで、「取り出したカードのスートはハートである」という事象と「取り出したカードの数字は4である」という事象の二つを考えると、前者の情報量は log 4、後者は log 13 である。この両者の和は log 4 + log 13 = log (4×13) = log 52 となり、「取り出したカードはハートの4である」という事象の情報量と等しい。これは「独立した情報の和が、全体の情報量と一致する」という直感的要請に合致する。
そしてかかる確率空間のみを観察対象として「損失(最小二乗法における残差平方和)を最小限に抑える」アルゴリズムが機械学習理論という次第。「データそのもの(から導出される確率空間)を主要観察対象とする」とはそういうk事なんですね。
そして…
時は21世紀。鉄道網と汽船航路によって世界中の物流網が一つに結ばれた結果として史上初の国際恐慌が勃発して「1859年認識革命」の引き金となった様に、世界中のデータ・トラフィック網がインターネットによって一つに結ばれた結果「ビッグデータ革命」が勃発したという次第。
同時進行でゲーム・グラフィック画質進化の落し子としての「並列処理の化物」GPU(Graphics Processing Unit)進化があり、かかる特定演算力の飛躍的向上を背景に「情報量が2^10000=10^30のオーダーを超えて初めて本領を発揮する機械学習アルゴリズム」大規模言語システム(LLM=Large Language Models)が登場してきた訳です。
ここで興味深いのが情報理論の大源流たる統計力学が「$${10^{23}}$$の粒子の力学を統計学的に扱うジャンル」であり、もしかしたらその$${10^{23}}$$のオーダーを超えてから劇的にパフォーマンスが向上する事に意味があるかもしれない事。だとすればそれは「(サンプル数を無限に増やしていけば概ねの分布が回帰するとされる)正規分布レイヤー」の手前に詳細不明の未知のレイヤーが存在している可能性を示唆する事。
そして人類はそれにアプローチする道として既に「決定木+双曲空間」なる強力なツールを手に入れてる事。
今から思えば「テトレーションを研究する数学者」としての顔も備えたSF小説家ルディ・ラッカー((Rudy Rucker, 1946年~)が「ウェア・シリーズ(1989年~2004年)」に登場させた「人間の心の働きを完全にバックアップした結晶」フラクタルライト概念もまた、現代でなら(フラクタル理論ではなく)「決定木+双曲空間」のイメージで再構成されるのでは? 日本では河原礫「ソードアートオンライン」シリーズ(2000年~)や「アクセル・ワールド」シリーズ(2009年~)に援用され、意外と知名度が高い代物。もちろん設定もそのままの流用ではなく、むしろグレッグ・イーガン「順列都市(Permutation City,1994年)」やJ.P.ホーガン「仮想空間計画(Realtime Interrupt,1995年)」の様な1990年代ハードサイバーパンク系の影響が色濃いとも?
【補筆1】そして話は原点に…
ここでやっと話は私のnoteにおける最初の投稿に戻ってくる訳ですね。
「史上最初のSNS」Facebookは開設当初「各アカウントが特定の人物に紐づけられる状況下、そのプロファイルとネットでの行動足跡を観察する形でマーケティングが完結する」と考えた(「統計学者と母集団推定の時代」の発想そのもの)。
しかし実際には「匿名で好きな事がやり放題」のTumbrにトラフィックの過半数以上を奪われる惨敗を喫っしてしまう。マネタイズ戦略に失敗したTumbrの栄華は長くは続かず、やがてその人気はYoutubeやInstagramに推移。これは同様の「アカウント・オリエンテッド戦略(要するに信用ならない登録プロファイルなど重視せず(といかそもそも登録を求めず)、それぞれのアカウントの振る舞いそのものを観察するマーケティング戦略)」がネット通販サイトや動画配信サイトにも広まった結果でもあるが、この時点で既に「統計学者と母集団推定の時代」は終わり「データそのものを観察するしかない」新たな時代が始まっていたといえよう。
そう、本来なら鋭敏なマーケッターならFacebook社(現Meta)がInstagramを買収して「顧客が倍になりました」的発表が流れた時点で眉に唾して「何かがおかしい」と考え始めるべきだったのである(Facebook社は流出した若者層を取り戻しただけだが、もはやその事を証明する手段すらない)。まさにカール・マルクスが1857年恐慌勃発が革命の機運につながらなかった状況を目の当たりにして「世界が致命的な形で変わってしまった(ここでいう「統計学者と母集団推定の時代」が始まった)」事を察して戦略の全面見直しに入って生き延びた様に、パラダイムシフトとは概ねこういう形で始まるものである。
【補筆2】「シミュレーションの時代」の幕開け
天体や自然現象を主要観察対象とした「大数学者と大物理学者の時代」においては、観察対象と観察結果の関係が全単射なのがほぼ自明でした。

ところが「(集団の多重化や集合間流動性まである)任意の物理的実態の群」を主要観察対象とする様になった「統計学者と母集団推定の時代」や「機械学習と意味分布論の時代」には普通に全射関係や単射関係が自明の場合として自然に混じってきます(ちなみに多様体による座標系埋め込みが可能なのは「微分結果が単射」の場合のみ)。

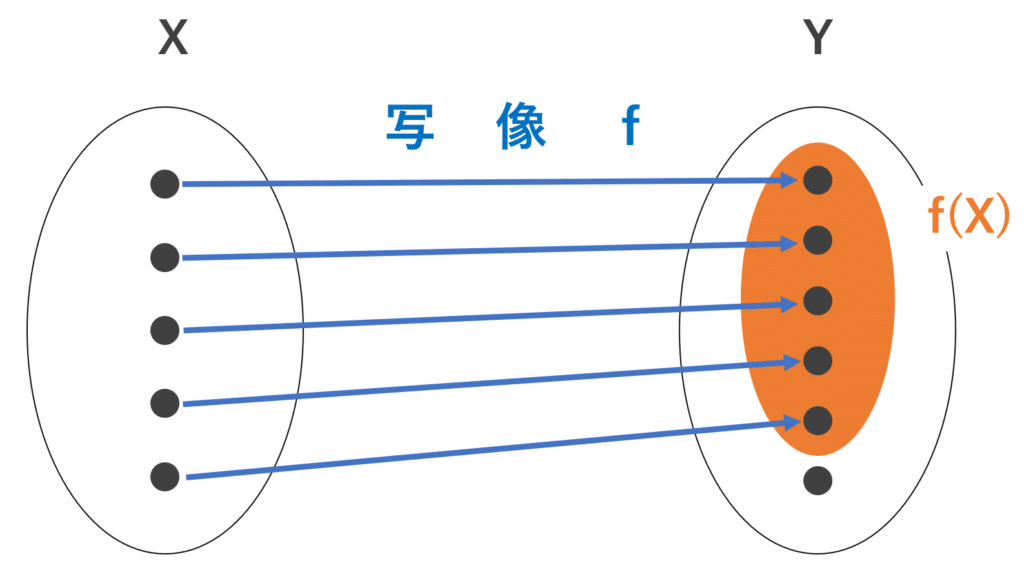
そしてさらに「機械学習と意味分布論の時代」には「特定の観測結果が特定の物理対象と紐付けられている」原則すら揺らぎ始めてしまうのです。
既に「大数学者と大物理学者の時代」の誤差関数や「統計学者と母集団推定の時代」の正規分布検定の世界においても「(外れ値に弱い最小二乗法の弱点を補う為に)極端な外れ値を検出して抜く」操作が採用されていたが、「機械学習と意味分布論の時代」には過学習を防ぐ為「ランダムに観測データを落とした集計データ同士を比較する」「故意に手ブレを起こして見掛け上のサンプル数を増やす」といった技法が開発された。ただまぁここまではギリギリ「特定の観測結果が特定の物理対象と紐付けられている」範疇に収まっていると言えなくもない。
「一定の計算手順によって確定的に与えられる疑似乱数」を「観測対象」とするケースも多い「データを1つづつ追加する過程で分類や順序を生成する」マルコフ連鎖モンテカルロ (MCMC=Markov Chain Monte Carlo) 法辺りからはそうもいっていられない。この様にコンピューター・シミュレーション要素が入ってきて話がややこしくなるのが、「機械学習と意味分布論の時代」の最大の特徴という訳である。

その一方で、最近話題の大規模言語モデル(LLM=Large Language Models)の観察対象は「ネット上で検索可能なテキスト群そのもの」、画像生成AIの観察対象は「ネット上で検索可能な画像群そのもの」となり、どちらもそれぞれ一応は「現実に存在する物理的存在(すなわちそれをネットに投稿した人間)」から切り離されてしまっており、しかもその復元を目的ともしていない。
大規模言語モデル(例: GPTシリーズ)の主要な観察対象と観察目的は以下の通りです。
生成能力と品質の評価:言語モデルがどれだけ自然なテキストを生成できるかを評価します。生成されたテキストの流暢さ、文法的正確さ、意味の適合性などが評価されます。
文脈理解の評価:モデルが与えられた文脈を理解し、それに基づいて適切な文を生成できるかどうかを評価します。例えば、質問に対する回答の適切性や、特定のトピックに関する情報の適切性などが含まれます。
多様性と一貫性の評価:モデルが多様な文を生成できるかどうか、また生成される文が一貫性を持っているかどうかを評価します。多様性が低い場合、モデルが同じような表現を繰り返し生成する可能性があります。
感情やスタイルの表現:モデルが感情やスタイルを適切に表現できるかどうかを評価します。例えば、文のトーンや感情、スラングやジャーゴンの使用などが含まれます。
外部知識の利用:モデルが外部の知識源(辞書、百科事典、ウェブなど)を適切に活用して生成する能力を評価します。外部知識の正確性や適切性が含まれます。
解釈可能性:モデルが生成したテキストや予測の理由を解釈することができるかどうかを評価します。これにより、モデルの意思決定の透明性や説明性が向上し、信頼性が高まります。
これらの観察目的に基づいて、大規模言語モデルの性能や特性を評価し、改善するための研究が行われています。
まだまだ全然舌足らずですが、これまで考えてきた事のとりあえずのまとめくらいにはなったのでメモがてら投稿。そんな感じで以下続報…
