
【数理的溢れ話24パス目】、「ミクロコスモス(泡沫事象)とマクロコスモス(事象全体)の照応(Anaphora)」問題と「中央値と外れ値」問題の挟間にて。
それまで「(同じ観測原点から出発しながら、それぞれ目指す方向が微妙に異なる事から)誰の進路も交わらない」情景をテーマとしてきた「何処にも辿り着けない」米津玄師が、「シン・ウルトラマン(2022年)」の主題歌「M87」では「(どんなに目指す方向が違っているとしても)それぞれが迷わず真っ直ぐ進み続ければ、無限遠点で再会出来る」と歌ったのは私にとって衝撃でした。それがまさに「(リーマン球面の概念とコーシー分布の概念をアークタンジェントの数理を用いて統合する)ガウス無限遠座標系」の考え方だったからです。
全ての出発点としての「ガウスの無限遠座標系」
その全体像を図示するとこんな感じになります。


とはいえこの座標系、「ミクロコスモス(泡沫事象)とマクロコスモス(事象全体)の照応(Anaphora)」があって数理処理に限界がある(あるいは数理処理の限界を示す)側面を備えているのが厄介。

①泡沫事象側には事象全体側そのものを直接認識する方法が存在しない。逆をいえば、泡沫事象の属する「数え上げ可能な世界」を超越して式∞±可算数d=∞が成立して以降が事象全体の領域となる。
要するに「1,2,…沢山」の世界。
この構造ゆえに任意の泡沫事象は、計算上そのそれぞれが観測原点0であると想定せざるを得ない。
②一方、事象全体側にはそれぞれの泡沫事象の相対位置を直接特定する方法が存在しない。逆をいえば、泡沫事象の属する「数え上げ可能な世界」を超越して式∞±可算数d=∞が成立して以降が事象全体の領域となる。
「60秒全体から俯瞰すると59秒や61秒との差はないに等しく(♾️±1=♾️)、かつどの元が増減したか見極めるのが難しい」世界。
「N進法における桁上がり/桁下がり(分単位の計算精度においては秒単位の位置まで観測出来ない)」)の世界。
全体として「普通は59分も61分もほぼ1時間と感じるが、そのうちどれかの1分が突如秒単位の注目対象に格上げになる事もある」という構図。任意の泡沫事象を対象として認識してるかしてないかのギリギリの境界線イメージ。
③それにも関わらず「部分が全体を被覆している」条件が成立しなければ集合として扱えないので、とりあえず式∞×1=1x∞は常に成立すると想定せざるを得ない(泡沫事象と事象全体の非対称性)。
④そして、かかる非対称性にも関わらず、連続のうちにその双方の片端が無限遠点に接続する為、泡沫事象と事象全体は可換である(泡沫事象と事象全体の対称性)。なおその可換性は以下の3種類によって構成される。
$${e^{x}(0≦x≦+∞)}$$と$${e^{x}(-∞≦x≦0)}$$の可換性(符号による分割)。

$${e^{+x}}$$と$${e^{-x}}$$の可換性(符号による交換)。

自然指数関数$${e^{x}}$$と自然対数関数$${\log_e(x)}$$の可換性(XY交換)。

まさしくこの情景こそが冒頭で述べた「(どんなに目指す方向が違っているとしても)それぞれが迷わず真っ直ぐ進み続ければ、無限遠点で再会出来る」世界観。かかる「ミクロコスモス(泡沫事象)とマクロコスモス(事象全体)の照応(Anaphora)」の全体像は、同様に荒川宏の漫画「鋼の錬金術師(2001年~2010年)」に登場する錬金術の原則「一は全、全は一」の世界観へも射影可能です。すなわち「世界全体を捉えた座標系から俯瞰すると、一(泡沫事象)を被覆しない全(事象全体)も、全(事象全体)の部分集合として存在しない一(泡沫事象)も、共に無意味である(存在しないに等しい)」なる信念こそが出発点。
とりあえず(閉世界仮説を成立させる為に)「さらなる外側」については完全視野外に追いやるという宣言でもあります。というか、これよりさらに外側を想定するのは到底人間には不可能とも?
宗教問題や哲学問題への突入を回避する為、科学実証主義の世界はこの座標系における「泡沫事象と事象全体の可換性」を以下の様に場合分けして考えなければいけません。
「相似性」次元からのアプローチ…「泡沫事象と事象全体は原則として相似だから原則として可換である」なる帰無仮説から出発し、その交換にともなう差分に優位差がないか調べる(例:「観測原点と観測対象」「個人と社会」「人間集団とそれ以外」など)。
「連鎖性」次元からのアプローチ…「1時間は60分。1分は60秒」「係を束ねるのが課で、課を束ねるのが部」といった連鎖関係に泡沫事象と事象全体の関係を射影したモデルを帰無仮説とし、任意の評価次元における差分に優位差がないか調べる(例:小集団と大集団の振る舞い上の違い、観察対象区間の地域サイズや時間サイズの変更に伴う変化など)。ベイズ統計学は、こうした条件の削減や追加に伴う条件付確率分布の変化を追うのに適している。
「置換性」次元からのアプローチ…「ミクロコスモス(泡沫事象)とマクロコスモス(事象全体)の照応(Anaphora)」概念は、iPhoneが登場してノキアのSymbian OSやDOCOMOのiModeやAuのEzwebが一瞬にして歴史の掃き溜め送りとなる一方、GoogleのAndroidの急追を受けてスマートフォン市場の独占自体には失敗した様な「(単なる条件の削減や追加に留まらない)条件そのものの置換を伴うベイス更新」展開を含む。いわゆる「ブラックスワン」現象で、逆をいえば「その様な変化は起こらない」と仮定するのが原則としてこの帰無仮説の棄却を目指す座標モデルの出発点に。
そして、ここに出てきた「ミクロコスモス(泡沫事象)とマクロコスモス(事象全体)は相似的で連鎖性があり置換可能である」なる帰無仮説の棄却過程は、機械学習アルゴリズムにおける「特徴抽出(Feature Extraction)」すなわち「マクロコスモス(世界=事象全体)」からのミクロコスモス(個性=泡沫事象)」の分離(Separation)作業とも深く関係してきます。そこでまず問われるのはどちらも「適切な評価次元が設定されているか(あるいはその設定の発見そのものが最初の課題)」という訳ですね。
なおここまでの考えは、昨年10月時点における以下の考え方をより発展させた結果でもあります。
ただしこの方法論だと証明能力辺りが一切身につかないのでルベール測度論あたりで容赦なく躓くのが確定となる。「1個の無限は無限個の1で被覆される。ならば1は無限個の0(1/∞))で被覆し得るのか?」みたいな壁が次ぐ次と現れ、いわゆる「確率の古典的定義」の破綻が始まってしまうので。
ルベール測度論は相変わらずサッパリのままですが、こう考えれば当面の問題は解決? その意味合いにおいては進捗は全くないでもない…
「ガウスの誤差関数座標系」及び「フイッシャーの有意水準座標系」「ベイズ更新座標系」の登場
ここまでの考え方は大数の法則(LLN=Law of Large Numbers)や中心極限定理(CLT=Central Limit Theorem)を一切含まず、そもそもそれぞれの泡沫事象は「'(計算上の原点としての)コーシーの主値」概念こそ備えるものの、それがそれぞれの座標系における代表地として機能してしまう為に、平均(Mean)の計算が不可能。そして平均の計算が不可能である以上、分散(Variance)もまた計算不可能となってしまいます。
一方、近代統計学はある段階まで「ブラックスワン現象が起こらない単一評価次元上において」「大数の法則=中心極限定理成立を前提として」中央値と外れ値の算出に血道を上げてきました。例えば「言葉をベクトル化して、その頻度分布と条件付同時出現分布から分布意味論的座標系を構築する」自然言語処理(NLP=Natural Language Processing)の観点から出発すれば、自明の場合として以下の様な展開となります。
中央値と外れ値自体は原則として「出現頻度分布」の濃淡によって自動的に定まる。
ただしここでいう出現頻度分布は大きく「条件付同時出現分布」の掣肘を受ける為、評価次元設定の影響を大きく受ける。
とはいえ近代数学が出発した時点では「条件付同時出現分布の掣肘」をそれほど強く意識する必要はなかったのです。何故なら主要な観察対象が「天体なる巨大な単一物」限られていたからです。
「ガウスの誤差関数」と正規分布の登場(19世紀前半)
フランス革命(1789年~1799年)の最中に「メートル法=地球の大きさに準拠する新しい単位」制定の機運が生じ、最小二乗法や誤差関数の様な新しい計測技術が樹立しました。
当時の論争ではラプラスが1799年に発見した最小一乗法に対してガウスの推す最小二乗法が圧倒的勝利を飾る展開となりましたが、最近は「中央値が平均と大きくズレる場合には最小一乗法が有効」と考える最小N乗法論が主流に。ただし「最小零乗法」および「最小三乗法」以上は捗々しい成果をあげていない。
最小二乗法のもう一つの問題点は平均値に拠る基準ゆえに外れ値の影響を濃厚に受ける事で、この問題点を緩和する為に誤差関数の技法を同時開発する必要が生じた訳である。
歴史のこの時点における観測対象は天体なる巨大な単一物であり、評価次元は物理距離のみですから「測定誤差=手ブレの様なもの」という認識。

小さな手ブレ(誤差)ほど比較的観測され易い。
大きな手ブレ(誤差)ほど比較的観測され難い。
従って、一定以上の誤差を切り捨てる事によって観測精度(Observation Accuracy)を確定する事が出来る。
ガウスはとりあえずこの「手ブレ(誤差)」が放物線$${y=x^2}$$上に分布すると考え、その指数写像の面積を求めました(いわゆるガウス積分)。
$$
\int_{-∞}^{+∞}e^{-x^2}dx=\sqrt{π}
$$
そしてこの考え方に基づいて誤差関数(ERF=Error Function)の概念を樹立したのです。
$$
erf(x)=\frac{2}{\sqrt{π}}\int_{-∞}^{+∞}e^{-x^2}dx
$$

これは-1から+1にかけての分布なので1足して2で割り0から1にかけての分布に正規化したのが標準正規分布(standard normal distribution)(x;0,1)の累積度数関数(CDF=Cumulative Distribution Function )F(x;0,1)となります。
$$
F(x;0,1)=\frac{1}{2}(1+erf(\frac{x}{\sqrt{2}}))
$$
さらにこの累計度数関数を微分すると標準正規分布の確率密度関数(PDF=Probability Density Function)f(x;0,1)が得られます。
$$
f(x;0,1)=\frac{1}{\sqrt{2π}}e^{-\frac{x^2}{2}}
$$
さらに使い勝手を増す為、パラメーターとして分布の平均値μと分散$${σ^2}$$を与えたのが、統計学を少しでも齧った事がある人間にとっては見慣れたこの形。
標準分布(累積分布関数)
$$
F(x;μ,σ^2)=\frac{1}{2}(1+erf(\frac{x-μ}{\sqrt{2σ^2}}))
$$

正規分布(確率密度関数)
$$
f(x;μ,σ^2)=\frac{1}{\sqrt{2πσ^2}}e^{-\frac{(x-μ)^2}{2σ^2}}
$$

この展開はこうも説明可能ですね。

まさしく「ブラックスワン現象が起こらない単一評価次元上において」「大数の法則=中心極限定理成立を前提として」中央値と外れ値の算出に血道を上げるアプローチの原風景。こうして「ガウスの無限遠座標系」を帰無仮説として棄却する形で「ガウスの誤差関数座標系」が成立する運びとなりました。とりあえずここに評価次元が適切な一次元に絞れたとして、その範囲内ではブラックスワン現象は起こらないと仮定した「より確固とした「1」概念(およびそれを計算単位とする可算座標系)」が成立した訳です。

それにつけても何故$${x^2}$$だと都合が良いのでしょうか? ガウスはかず多くの例を挙げましたが、その中に後世にまでコンセンサスとして語り継がれる様な強力な説は含まれていませんでした。なので以下はあくまで私見に過ぎませんが、例えば円錐座標系上において「ガウスの無限遠座標系」$${e^{πi}}$$を底面=静止衛星軌道と置くと、それを45度傾けた放物線$${x^2}$$は脱出軌道に該当します。もしかしたら「それ以上は切り捨てて考えて良い」と規定する合理的理由はこの辺りに潜んでいるのかもしれません。つまり数学自体というより物理学からのインスパイアであったのではないかという考え方。

日本の和算は、例えば18世紀時点においては微積分計算分野でニュートン(Sir Isaac Newton,1642年~1727年)やライプニッツ(Gottfried Wilhelm Leibniz, 1646年~1716年)に追いつかんばかりの研究成果を残しています。その一方でとうとうこの領域には一歩も踏み込む事がありませんでした。当時の欧州においては日本と異なり数学者が物理学者や天文学者を兼ね、天体軌道や地球の距測事業に積極的に関わっています。この辺りが両者の明暗を分けたとしか考えられない訳です。
「統計革命」と「優性主義」概念の興亡(19世紀後半~20世紀前半)。
産業革命導入が本格化した19世紀後半に入ると、統計学の目的は「巨大な単一の観測対象の観測誤差除去」に限らなくなってきます。それでも工場の品質管理問題くらいなら「ガウスの誤差関数座標系」に立脚して誤差を除去するイメージの延長で何とかなってた様ですが…ガウスが発見した正規分布の概念があらゆる森羅万象の諸現象の中に普遍的に見出せると主張したのは英国の数理統計学者カール・ピアソン(Karl Pearson,1857年~1936年)が最初だったとされています。
決定打となったのは兄弟弟子ウォルター・F・R・ウェルドン(Walter F. R. Weldon,1860~1906年)との共同研究「進化の数学理論への貢献(1894年)」において示された「イタリアのナポリに生息するあるカニの個体999匹の甲羅のサイズ分布」.辺りだったとされています。まぁ確かに言われたら正規分布している様に見えなくもありません。

計算内容は全く同じなのだが、この間に「外れ値」の内容が「大数学者と大物理学者の時代」末期(19世紀前半)の「巨大な単一物の観測データのズレ」から「産業革命浸透期(19世紀後半)」における「大量生産課程における規格外不良品」を経て「恣意的評価次元において群全体の中央値から想定以上に離れた個体」へと推移。現代人の感覚では、この様に次第に評価軸設定上の恣意性が増す一方で切り捨て対象が実体性を帯びていく過程に当時の人間はあまりにも無頓着過ぎた様に映る。
なおこの投稿は、以下の投稿における時代区分①数秘術師や魔術師の時代(イタリア・ルネサンス期~近世)。②大数学者や大物理学者の時代(大航海時代~1848年革命の頃)。③統計学者と母集団推定の時代(産業革命時代~現代)。④機械学習と意味分布論の時代(第二次世界大戦期~現在)で十分言及出来なかった「統計学者と母集団推定の時代」の補完でもある。
まさにこの瞬間、「巨大な単一の天体上の表面距離の観測誤差除去」問題が「群の分布をその中央値分散で測る」発想に飛躍するコペルニクス的転回が発生。この流れが俗にいう「統計革命」第一波となった訳ですが、同時にこの頃から次第に「条件付同時出現分布の掣肘」が次第に頭をもたげてくる展開を迎えます。例えばPythonライブラリーに収録されている「ペンギン」データセットに目を向けてみましょう。このデータセットには以下のデータが収録されていて、様々な評価次元で相関係数などが計算可能となっています。

そう、観測対象が巨大な単体から群の一匹一匹に推移しただけでなく、その評価次元も一気に多次元化してどれを代表に選ぶか自体から頭を捻らざるを得なくなったのです。しかも「ペンギンの成長記録」なら尺度の方向も概ね揃っていますが、全ての分布にこの考え方が当てはまるとは限りません。そこを強引に、例えば人間集団の分布について「片側に天才の様な優秀な人材が、もう片側に犯罪者や精神異常者の様な劣等な人材が現れる正規分布」と捉えようとしたら? もしその人間集団について「優秀な人材を増加させつつ、劣等な人材を減らしていく」方法が発見されたら、その人間集団の改良に役立つのでは? それがまさに当時大流行した優生学の発想であり、カール・ピアソンもまたそう考える優生学者の一人だったから話がややこしくなってくるのです。
とはいえ歴史のこの時点で「天才同士を掛け合わせて天才を増やす」発想自体はすでに頭打ちになっていた。彼の師匠に当たる優生学者フランシス・ゴルトン(Sir Francis Galton, 1822年~1911年)が既に「平均回帰の法則」到達していたからである。
また19世紀後半に猛威を振るったチェーザレ・ロンブローゾ(Cesare Lombroso, 1835年~1909年)の「生来犯罪者説」もガブリエル・タルド(Jean‐Gabriel de Tarde, 1843年~1904年)の「模倣犯在学」圧倒され、その勢いを無くしていた。
極め付けは障害者や精神病患者や(当時はその同類と看做されていた)同性愛者をホロコーストによって淘汰しようと試みたNSDAPの蛮行で、その多大な人的被害にも関わらず実際にはドイツ民族が改良された形跡は一切見られなかったのである。
まさにかかる形でのNSDAPによる優生学理論採用が「優生学の時代」に終焉をもたらしたといっても過言ではありません。
1930年代に入りカール・ピアソンが事実上引退すると、彼が築き上げたロンドン大学の生物測定学科は2つに分割され、ロナルド・フィッシャー(Sir Ronald Aylmer Fisher, 1890年~1962年)が新しくできた優生学科の学科長に就任します。同時期、縮小された生物測定学科には「カール・ピアソンの息子」エゴン・ピアソン(Egon Sharpe Pearson, 1895年~1980年)が就任します。その後、優生学科はナチスに繋がるものとして、第2次世界大戦と同時に解体されてしまいます。
統計学理論自体はこうした歴史的過程とは一見無縁の発展を遂げています。
カール・ピアソン、ロナルド・フィッシャー、エゴン・ピアソンは、それぞれ統計学において重要な貢献をした著名な統計学者です。彼らは統計学の発展に異なる方法で影響を与え、現在の統計理論に大きな影響を及ぼしました。
1. カール・ピアソン (Karl Pearson, 1857–1936)
カール・ピアソンは、近代統計学の基礎を築いた人物であり、特に数理統計学の確立に貢献しました。彼の業績は以下の点で注目されます。
相関係数の導入: ピアソンは、2つの変数間の線形関係を測定するための相関係数(Pearson's correlation coefficient)を導入しました。これは現在でも広く使用されている基本的な統計手法です。
ピアソンのカイ二乗検定: カイ二乗検定(χ²検定)は、観察されたデータが期待値と一致するかどうかを評価するための統計検定です。ピアソンは、この検定方法を発展させ、適合度検定や独立性の検定に使用される手法を確立しました。
生物統計学の発展: ピアソンは進化論と遺伝学に基づいた生物統計学の分野を開拓し、進化や遺伝の統計的分析に大きく貢献しました。
彼の功績により、統計学が科学的なデータ分析に不可欠なツールとなり、現代の統計学の基盤を築きました。
2. ロナルド・フィッシャー (Ronald A. Fisher, 1890–1962)
ロナルド・フィッシャーは、現代の統計学と遺伝学に革命をもたらした統計学者で、推測統計学や実験計画法において多大な貢献をしました。
フィッシャーの分散分析(ANOVA): フィッシャーは、実験結果の解釈に重要な手法である分散分析を開発しました。これは、複数のグループ間の平均の差異を評価するための統計手法で、農業実験や多くの分野で応用されています。
最大尤度法: フィッシャーは、統計的推測において広く使用される最大尤度法(Maximum Likelihood Estimation, MLE)を導入しました。この方法は、観察されたデータから最も確からしいパラメータの値を推定する手法で、統計モデリングの基盤となっています。
推測統計学の発展: フィッシャーは、推測統計学において信頼区間や仮説検定の概念を確立しました。彼の研究により、統計的推論が科学的なデータ分析の重要な部分となりました。
フィッシャーのF検定: フィッシャーの名にちなむF検定は、分散分析や多変量解析において、2つ以上のグループ間の分散の比率を比較する手法です。
フィッシャーの業績により、実験デザインやデータ解析の方法論が大きく進展し、今日の統計学の基礎が確立されました。
3. エゴン・ピアソン (Egon Pearson, 1895–1980)
エゴン・ピアソンは、カール・ピアソンの息子であり、統計学においても重要な役割を果たしました。彼は特に、統計的仮説検定の分野における業績で知られています。
ネイマン=ピアソンの補題: エゴン・ピアソンは、イェジ・ネイマン(Jerzy Neyman)と共に仮説検定の理論を発展させ、最も強力な統計的検定を導くための基礎であるネイマン=ピアソンの補題を提唱しました。この理論は、帰無仮説と対立仮説を比較する際に、誤差のリスク(第一種過誤と第二種過誤)を最小化するための方法論を提供します。
仮説検定の枠組み: ネイマン=ピアソンの仮説検定は、統計学において決定論的なアプローチを採用し、実際のデータからどの仮説が採択されるべきかを導くための体系的な方法を確立しました。これは今日でも広く使われている統計的検定の基礎となっています。
エゴン・ピアソンの仮説検定の理論は、実験結果やデータから意思決定を行う際の基盤となっており、現代の統計学において不可欠な概念です。
まとめ
カール・ピアソンは、相関係数やカイ二乗検定など、統計学の基礎的な手法を確立し、近代統計学の礎を築きました。
ロナルド・フィッシャーは、分散分析や最大尤度法、推測統計学の発展に大きな貢献をし、実験デザインや統計的推論に革新をもたらしました。
エゴン・ピアソンは、ネイマン=ピアソンの仮説検定理論を提唱し、統計的検定の枠組みを整え、実際のデータに基づく意思決定を行うための重要な手法を提供しました。
この3人は、それぞれの時代において統計学の発展に不可欠な役割を果たし、今日の統計理論と応用に深い影響を与えました。
厳しい言い方をすると、優生学の影響が最も著しかったフランシス・ゴードンやカール・ピアソンの時代の統計学はまだまだ分布の異同を調べるのが精一杯で記述統計学の域を抜け出していなかったとも。
記述統計学と推定統計学の歴史は、それぞれ異なる目的と手法を発展させながら、統計学の重要な分野として現在に至っています。以下では、両者の歴史的背景と発展について概観します。
記述統計学の歴史
記述統計学は、データを整理し、要約し、わかりやすく提示するための手法を扱う分野です。平均、中央値、標準偏差、ヒストグラムなどの基本的な統計指標を通じて、データの特徴を明らかにします。この分野の歴史は古代にまで遡ることができ、次第に発展してきました。
1. 古代から中世
統計学の起源: 統計の語源は、ラテン語の "status" に由来し、国家や社会の状況を記録するための情報を意味しました。紀元前から古代エジプトや中国、ローマなどで、人口や農業、税収に関する情報を記録し、整理していた記録が残っています。これらは後の記述統計学の基礎となりました。
中世のヨーロッパ: 人口調査や税務管理は中世にも行われており、国家運営のために数値を記録し、整理する技術が発展していきました。
2. 17~18世紀の発展
国家統計の誕生: 17世紀に入ると、特にヨーロッパでは国家の統治に必要なデータを記録する「国家統計」が発展しました。ドイツでは、この分野を「Staatswissenschaft」(国家学)として制度化しました。
ジョン・グラント: 1662年、イギリスのジョン・グラントは『ロンドンの死亡統計』という画期的な書を出版し、初めて人口の出生率や死亡率を数理的に分析しました。これが人口統計学の始まりとなり、後の記述統計学の基礎となりました。
3. 19~20世紀の発展
フランシス・ガルドン: 19世紀のイギリスの生物学者フランシス・ガルドンは、遺伝学の研究を通じて統計的な手法を発展させ、標準偏差や回帰分析といった概念を確立しました。
カール・ピアソン: カール・ピアソンはガルドンの研究を発展させ、相関係数や分布の標準化など、現代的な記述統計学の基礎となる概念を確立しました。彼の貢献により、統計学はデータの分析と整理を通じて科学的に物事を理解するための重要な手段となりました。
推定統計学の歴史
推定統計学は、サンプルデータから母集団の特性を推定するための手法を扱います。推定統計学は、20世紀初頭に確立され、記述統計学に比べて比較的新しい分野です。
1. 18~19世紀の始まり
確率論の誕生: 推定統計学は、確率論にその起源を持ちます。確率論は17世紀にパスカルやフェルマー、ライプニッツなどの数学者たちによって発展し、ギャンブルや不確実な事象を数理的に扱うための理論が確立されました。これが後の推定統計学の基礎となりました。
トーマス・ベイズ: 18世紀の数学者トーマス・ベイズは、条件付き確率に基づいた推定方法、いわゆる「ベイズ推定」の理論を確立しました。これは、現代におけるベイズ統計学の基礎です。
2. 20世紀初頭の革新
ロナルド・フィッシャーの貢献: 20世紀初頭、ロナルド・フィッシャーは推定統計学の確立に決定的な役割を果たしました。彼は、最大尤度法(Maximum Likelihood Estimation, MLE)を導入し、サンプルから母集団のパラメータを推定する方法を開発しました。また、仮説検定や信頼区間の概念を確立し、データに基づく推論を行う手法の基盤を築きました。
ネイマン=ピアソンの仮説検定: イェジ・ネイマンとエゴン・ピアソンは、フィッシャーの研究を基に、仮説検定に関する理論的枠組みを完成させました。これにより、帰無仮説と対立仮説を比較する際に、第一種過誤と第二種過誤を考慮した検定手法が確立されました。
3. 現代への発展
ベイズ統計の復興: 20世紀後半に、ベイズ統計学が再び注目されるようになりました。コンピュータ技術の発展により、複雑なデータ解析や推論が可能になり、ベイズ推定を利用した統計的手法が広範に使用されるようになりました。
統計的モデリング: 現代の推定統計学は、回帰分析や一般化線形モデル(GLM)など、さまざまなモデリング手法を使用して、データから母集団の特性を推定する技術を高度に発展させています。
まとめ
記述統計学は古代から国家運営のためのデータ整理として発展し、19世紀にガルドンやピアソンによって科学的な分析手法が確立されました。これはデータの整理、要約、可視化を行うための基礎的な統計学です。
推定統計学は、18世紀の確率論に端を発し、20世紀初頭にロナルド・フィッシャーやネイマン、エゴン・ピアソンらの理論的貢献によって確立され、サンプルから母集団の特性を推定する方法論を発展させました。
このように、記述統計学はデータの特徴を要約するための技術であり、推定統計学はサンプルデータに基づいて母集団の性質を推論する技術として発展してきました。両者は統計学の基礎を形成しており、現代のデータ解析や科学的推論に不可欠な要素です。
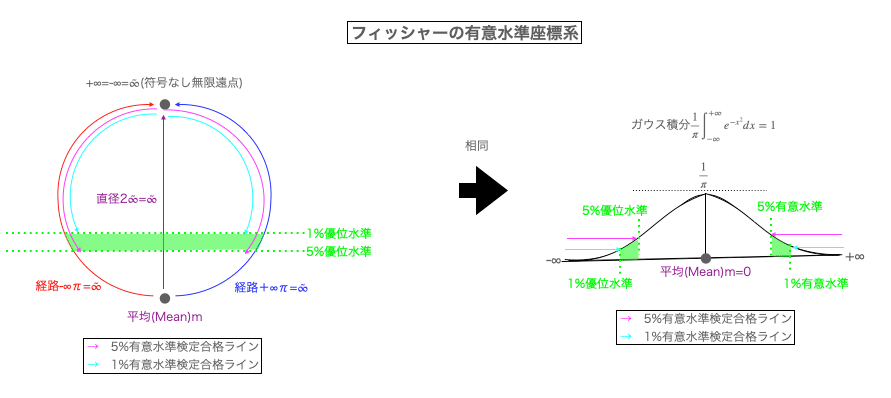
「誤差から分布へ」なるコペルニクス的転回に引き続いて「統計革命」第二波を引き起こしたのはロナルド・フィッシャーだった。「何も特別な事は起こってない」と考えられる帰無仮説を有意水準と観測結果のP値(帰無仮説における珍しさ)の比較によって棄却する考え方を導入し、目安となる湯有意水準として「5%水準」や「1%水準」を定めた。ガウスの時代における「除去対象としての手ブレ(誤差)」概念は、この時代以降、真逆に「帰無仮説を棄却するに足る観測結果の珍しさ」とも考えられる様になっていく。「ガウスの誤差関数座標系」とは真逆の「1」の規定方法。これをここでは「フィッシャーの有意水準座標系」と呼ぶ事にしよう。
度々、議論になるp値… pic.twitter.com/ui7hE4Fwn6
— kenken (@kenken26679105) June 11, 2024
さらにイェジ・ネイマン(Jerzy Neyman, 1894年~1981年)と組んでP値設定や対立仮説を用意する仮設検定理論を洗練させ、(帰無仮説が真なのに棄却されてしまう)第一種過誤や(帰無仮説が偽なのに棄却されない)第二種過誤をも意識して頻度主義統計学の検定理論を現在採用されているレベルに引き上げたのが「カール・ピアソン息子」エゴン・ピアソンであった。
こうして「ガウスの誤差関数座標系」を帰無仮説として棄却する形で成立したのが「フイッシャーの有意味水準座標系」となる訳です。
しかしながら当時の統計革命には「同じ様な条件下で観測されたデータが複数存在し、そのうちどれが代表的分布か判断する」農学・医療系研究が盛んだったのを背景に頻度主義統計学ばかりに注目しベイズ統計学を黙殺した負の側面も存在したのです。特に1930年代から1940年代にかけての「ベイズ主義者」ハロルド・ジェフリーズ(Sir Harold Jeffreys、1891年~1989年)への「頻度統計主義者」ロナルド・フィッシャーの執拗な攻撃は統計学の歴史に深い爪痕を残したといわれています。
ロナルド・フィッシャー(頻度主義統計学の代表者)とハロルド・ジェフリーズ(ベイズ統計学の支持者)は、20世紀前半に統計学の基礎に関する重要な議論を展開しました。この議論は、頻度主義統計学とベイズ統計学の基本的な考え方の違いに基づいており、特に推定の方法論や確率の解釈に焦点が当てられました。
頻度主義統計学とロナルド・フィッシャーの立場
ロナルド・フィッシャーは、推定統計学と仮説検定の枠組みを確立した一方、頻度主義的アプローチに基づいた確率の解釈を提唱しました。頻度主義統計学は、次のような立場を取ります。
確率の解釈: 確率は、特定の事象が無限回の試行の中でどれだけ頻繁に起こるかという頻度に基づいて定義されます。これは客観的な確率の定義であり、事象が繰り返し起こる試行に基づいてのみ確率を定量化します。
最大尤度法(MLE): フィッシャーは、推定統計において最大尤度法を強く支持しました。これは、観察されたデータに最もよく適合するパラメータ値を推定する方法であり、サンプルデータからパラメータを推定するための標準的なアプローチとして確立されました。
推論の客観性: フィッシャーは、統計的推論において主観的な要素を排除し、客観的でデータに基づいた推定方法が重要であると主張しました。特に、事前確率(prior probability)を使うことを批判しました。
ベイズ統計学とハロルド・ジェフリーズの立場
ハロルド・ジェフリーズは、ベイズ統計学を支持し、確率の主観的な解釈を重視しました。彼のアプローチは、事前情報と観察データを統合して意思決定や推定を行うというもので、ベイズ推論を中心に展開されました。
確率の解釈: ジェフリーズのベイズ統計学では、確率は主観的信念の度合いとして解釈され、特定の事象がどの程度発生するかの信念を表すものとされます。この信念は、事前確率と呼ばれる主観的な知識や仮定に基づいています。
ベイズの定理: ベイズ統計学は、ベイズの定理に基づいて推論を行います。観察データに基づいて確率分布を更新し、事後確率(posterior probability)を計算することで、データに基づいた最適な判断を行います。
事前確率の重要性: ジェフリーズは、特定の仮定や事前情報を反映した事前確率を使用することが、正確な推論や意思決定に役立つと主張しました。彼は、観察データに加えて、過去の知識や仮定を組み合わせることが推定の有効性を高めると考えました。
フィッシャーとジェフリーズの主な対立点
両者の議論は、主に次の3つの点で対立しました。
確率の解釈:
フィッシャーは、確率を客観的で繰り返し観測できる現象の頻度として捉え、主観的な確率の解釈を否定しました。彼は確率を観察可能な試行の長期的な頻度として扱うべきだと主張しました。
一方、ジェフリーズは、確率を主観的な信念や知識の反映として捉え、データや事前情報に基づいて確率を更新するベイズ的アプローチを支持しました。
推定方法:
フィッシャーは、最大尤度法(MLE)を推定の主要な手法として強く支持し、事前確率を含めたベイズ推定を批判しました。彼は、データに基づいてパラメータを推定する際に、客観性を確保すべきであると考えました。
ジェフリーズは、ベイズ推定を支持し、事前確率を活用して推定結果を改善できると主張しました。彼は、ベイズの定理を通じて、データと事前の知識を組み合わせることが有効だと考えました。
仮説検定の方法:
フィッシャーは、帰無仮説検定を強く支持し、観察データに基づいて帰無仮説の棄却を行う頻度主義的なアプローチを推奨しました。彼のアプローチは、p値に基づいて仮説を評価するものです。
一方、ジェフリーズは、仮説検定において事前確率を活用し、ベイズ的アプローチで仮説を評価するべきだと考えました。彼は、頻度主義の帰無仮説検定は不十分であり、ベイズ的視点から仮説を評価することがより合理的であると主張しました。
まとめ
ロナルド・フィッシャーとハロルド・ジェフリーズの議論は、統計学における頻度主義統計学とベイズ統計学の根本的な対立を象徴しています。フィッシャーは客観的な確率とデータに基づく推定を重視し、事前確率の使用に反対しました。一方、ジェフリーズは、確率を主観的な信念の度合いとして捉え、ベイズの定理に基づく推定と仮説検定を推奨しました。
この議論は、現在でも統計学の理論と実務に影響を与えており、両者のアプローチはさまざまな状況で使い分けられています。どちらの方法も利点があり、データ解析の目的や状況に応じて最適な手法を選択することが重要です。
支持するハロルド・ジェフリーズの間にどんな議論があったか教えてください。」
実際にはハロルド・ジェフリーズ側はロナルド・フィッシャーの最大尤度法(MLE)ベイズ統計学の間に連続性を認め、サンプルが十分大きい場合には最大尤を使う様な柔軟性を備えていましたが、ロナルド・フィッシャー側が意地でもベイズ統計学の有用性を一切認めなかったのです。カール・ピアソンが消極的ながら「実際的な人間なら、より良いツールが見つかるまではベイズ=ラプラス印の逆確率の結果を受け入れる事になる」と認め、ネイマンも若い頃は熱心なベイズ統計学の研究者だったのに対し、自らの研究環境に過剰適応したロナルド・フィッシャーは「統計学とは十分なデータが集まった場合のみ適用される厳密数学である」としか考えられなくなり、特に(十分な根拠が得られない場合には確率をサンプルサイズで均等割する)ベイズ統計学の「理由不十分の原理」を目の敵とする様になったのでした。
そうした硬直状態を打破したのが第二次世界大戦勃発でした。エニグマ暗号機の解読にベイズ統計学が必要となり、航空機を撃墜する「自動化された射撃統制システム」の開発が「マックスウェルの魔様な永久機関そのものは実現不可能だが、生命の営みはこれに類する準安定性を保ち、それは数々のフィードバック機構の組み合わせによって実現される」なる新しい考え方が台頭してきたのです。
20世紀後半はコンピューター普及に後押しされたベイズ統計学復権が著しかった時期で、この流れが事実上「統計革命」第三波
形成。ここではベイズ更新による構成次元数の増減が条件付確率に与える影響が帰無仮説としての「ガウスの無限遠座標系」を棄却する特徴に注目し、それを「ベイズ更新座標系」と呼ぶ事にする。

その一方でこの時代に整備された「分布の異同を判断する方法論」「出現頻度と条件付同時出現率分布の組み合わせによって構成される」幾何学習アルゴリズムにおいても現役で組み込まれていたりします。
分散分析(ANOVA, Analysis of Variance)は、統計学においてグループ間の平均の差を検定する手法ですが、この理論は機械学習アルゴリズムにもいくつかの重要な形で活用されています。以下では、具体的な応用例と、その背後にある考え方を説明します。
1. 特徴選択の一環としての分散分析
機械学習アルゴリズムの重要なプロセスの1つは、特徴選択です。特徴選択は、モデルのパフォーマンスを向上させるために、重要な特徴(変数)を選び出すプロセスです。ここで、分散分析の考え方が役立ちます。
ANOVA F検定: 分散分析のF検定は、数値特徴とカテゴリ特徴の関連性を評価するために使用されます。例えば、目的変数がカテゴリ変数であり、説明変数が連続変数である場合、ANOVA F検定を使用して、各説明変数が目的変数に対してどの程度の影響を持っているかを確認することができます。
応用例: 分類タスクにおいて、ANOVA F検定は特徴の有効性を判断するために使用され、重要な特徴だけを残すことにより、モデルの精度や計算効率を向上させます。
2. 回帰分析のモデル評価
分散分析は、機械学習における回帰モデルの評価や分解にも役立ちます。特に、回帰モデルのフィットの良さを評価するために、分散の分解を行い、説明可能な分散(回帰分散)と説明不能な分散(誤差分散)に分けることができます。
総平方和の分解: 線形回帰モデルにおいて、分散分析は次のように分散を分解します。
回帰平方和(SSR): モデルが説明できる分散。
残差平方和(SSE): モデルが説明できない残差に対応する分散。
総平方和(SST): 全データの分散。これがSSRとSSEに分解されます。
この分解は、回帰モデルがどの程度データを説明できているかを示す指標であり、モデルの決定係数 (R²) や他の評価指標の計算にも使われます。
応用例: 回帰タスクにおいて、分散分析を使ってモデルの予測精度や適合度を評価し、フィットの良さを判断します。
3. バイアス-バリアンストレードオフ
機械学習アルゴリズムのモデル選択において重要な概念に、バイアス-バリアンストレードオフがあります。これは、モデルの複雑さを調整し、過学習(オーバーフィッティング)や過少学習(アンダーフィッティング)を防ぐための考え方です。
バリアンスの解釈: 分散分析の「分散」の概念が、モデルのバリアンス(予測の揺らぎ)にもつながります。高度に複雑なモデルは、トレーニングデータに対して高い精度を持つ反面、新しいデータに対して過剰適合し、バリアンスが大きくなりすぎる可能性があります。これに対して、シンプルなモデルはバリアンスが小さいが、バイアスが大きくなります。
応用例: 決定木やランダムフォレストのようなモデルでは、木の深さやパラメータの調整によってバイアスとバリアンスをコントロールし、最適なモデルを選ぶ際にこのトレードオフを考慮します。
4. 交差検証でのモデル評価
分散分析は、交差検証を使ってモデルのパフォーマンスを評価する際にも関連します。交差検証は、データをいくつかのサブセットに分け、異なるモデルに対して複数の評価を行うことで、過剰適合や過少適合を防ぎます。これにより、モデルのパフォーマンスの一貫性を確認できます。
分散の測定: 交差検証の結果を分析する際、複数の評価結果間の分散を評価することは重要です。これにより、モデルの安定性や性能のばらつき(分散)が分かります。ここでも、分散分析の手法が役立ちます。
応用例: 交差検証結果の分散が小さいモデルは、データに対して一貫した性能を発揮することを示し、信頼性が高いとされます。
5. 分散分析を使ったハイパーパラメータのチューニング
機械学習アルゴリズムのハイパーパラメータの最適化においても、分散分析が役立つことがあります。特に、複数のパラメータの組み合わせや異なるモデルに対して、パフォーマンスの差を評価する際に、分散分析を行ってどのパラメータがパフォーマンスに有意な影響を与えるかを確認します。
応用例: ハイパーパラメータの異なる設定を比較して、それが結果に有意な影響を持つかを検定し、最適なパラメータの組み合わせを選びます。
まとめ
分散分析は、機械学習において次のような形で応用されています。
特徴選択:ANOVA F検定などで重要な特徴を選択する際に利用。
回帰分析の評価:モデルのフィットの良さや分散の分解を通じて、回帰モデルの性能を評価。
バイアス-バリアンストレードオフ:モデルの複雑さを調整し、最適なモデルを選択する際の指針。
交差検証:モデルの安定性や性能のばらつきを評価するための分散の測定。
ハイパーパラメータのチューニング:パラメータの違いによるパフォーマンスの差を評価。
これらの応用例を通じて、分散分析の考え方は機械学習において多様な方法で活かされています。
この形はこの形で大数の法則概念や中央極限定理概念から遠ざかっているのが興味深いところですね。
「マルクス=ピアスン主義」なる歴史的残滓
ところでカール・ピアソンが「Carl Pearson」でなく「Karl Pearson」名乗る様になったのはカール・マルクス(Karl Marx, 1818年~1883年)に傾倒して以降。ただし「資本論(Das Kapital. Kritik der politischen Ökonomie,,第1部1867年,第2部1885年,第3部1894年)」英訳を申し出て断られており、その思いは一方通行だった模様。
しかし、その考え方は案外後世に継承されてしまったのでは? そんな感じでとりあえず以下続報…
