【数理的溢れ話１パス目】数学の世界ではあまり語られない「パチンコ台やパチスロ台の出目の荒さ/穏やかさ(分布の尖度)」概念
以下の投稿の以下の脱線気味の注釈が全体の可読性を落としているので切り離す事に決めました。以降もそういう事態に対応する為の新シリーズです。
①ある現象が起こる確率($${0≦P_i≦1}$$)と、その条件($${(x_{i1},x_{i2},…,x_{in}),-∞≦x_{in}≦+∞}$$)のi個の集合からなるデータセットが存在するものとする。
ただし正規分布概念そのものが「いかなる評価軸上の分布バラつきも、評価軸を無限に増やし続けたなら必ず特定の唯一の分布に収束する」なるある種のニヒリズム思想(正規分布原理主義)に立脚している事だけは決して忘れてはいけない。この意味合いにおいて、ある意味20世紀はまさにこの「正規分布ニヒリズム」の時代であった。そして、だからこそ大規模言語モデル(LLM=Large Language Model)における「$${2^{10000}=10^{30}}$$パラメーターの壁」の発見が、21世紀世界に揺るぎない大衝撃を与える展開を迎えた訳である。
考えてみれば、そもそも20世紀に入ってから発案された分散概念そのものが背景に正規分布を想定しており、これの手を出した時点で推測統計の世界に足を踏み入れるとも考えられる。統計学や機械学習の教科書の多くは、こういう話についてちゃんと語ろうとしない傾向が見受けられる。
ところで統計学における期待値(Expected Value)Eの概念もまた、操作変数Xについて線形性を有するとされる。
$$
E[X_1+X_2]=E[X_1]+E[X_2]
$$
$$
E[\sum_{i=1}^nX_i]=\sum_{i=1}^nE[X_i]
$$
期待値概念を説明にはしばしば「くじ引き箱」の概念が用いられるが…
$$
E=p_1X_1+p_2X_2+p_3X_3+…+p_nX_n=\sum_{i=1}^np_iX_i
$$
$$
ただしp_1+p_2+p_3+…+p_n=\sum_{i=1}^np_i=1
$$
これ自体がもう正規分布におけるパラメーターの一つ「平均」の概念そのものだったりする。
だから、あえて「正規分布を前提とする」推測統計の世界に踏み込む覚悟さえ決めれば「分散」の概念を導入して分布の「尖度」を比較する事も出来る。実際パチンコやパチスロの様な確率依存遊戯機の攻略においては、機種による台の出玉を比較したり(例えば1990年代のパチスロだとクランキーコンドルが「尖度が大きい」荒い台、ジャグラーが「尖度が小さい」穏やかな台を代表)、出玉分布から設定を見抜く技法が磨かれてきた。
その一方で平均が中央でない場合には平均値と中央値と最頻値がバラけるという問題も発生。正規分布原理主義が支配的だった20世紀には誤差として黙殺され勝ちだったが、21世紀に入ってから急速に発達した機械学習の世界では、この辺りの数理も何とかして取り込もうという動きも見受けられる。
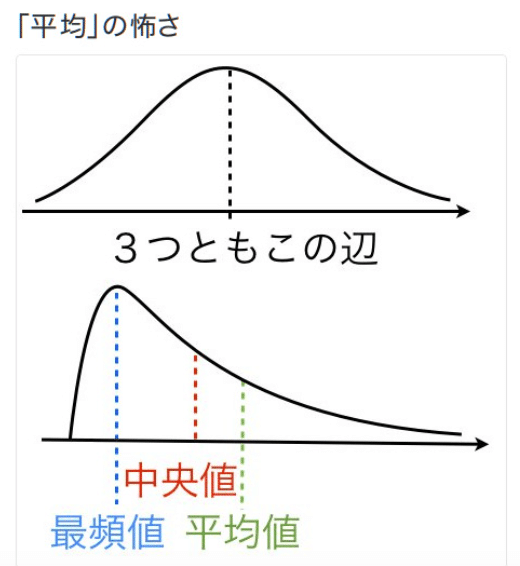
そんな感じで以下続報…
この記事が気に入ったらサポートをしてみませんか？