
【試論「人工知能概念はいつから存在したといえそうか?」10パス目】「ディープランニングはアフィン変換と見つけたり」?
今回の出発点はネットで見つけた以下の記事となります。
とりあえず簡便化の為にディープラーニング・アルゴリズムで処理される各データのライフサイクルを経路(route)$${R=\left[r_i\right]_{i=0}^n}$$の線型リスト形式で表現する事にしましょう。

入力層(Input Layer)=第0層
オーディオ機器などにおけるADC(Analog to Digital Converter=アナログデジタル変換回路)」に該当する処理で、システム外で遂行される「ニューラル・ネットワーク座標系へのデータ・プロッティング」の結果。
出力層(Output Layer)=第n層
オーディオ機器などにおけるDAC(Digital to Analog Converter=デジタルアナログ変換回路)」に該当する処理。「ニューラル・ネットワーク座標上のデータ集合」が統計学における最尤推定などの検定手段に引き渡される。
ただしディープラーニング・アルゴリズムは、無作為に統計学的検定手段によって有意水準の有無を確かめるのではなく「検定の結果、あらかじめ有意水準が出る様に調整されたデータ集合」を引き渡すのである。
機械学習と最尤推定(Maximum Likelihood Estimation, MLE)は深く関連しています。最尤推定は、多くの機械学習アルゴリズムの基礎となる統計的手法であり、モデルのパラメータをデータに最も適合するように調整するために使われます。以下に、その関係について詳しく説明します。
(中略)
結論
最尤推定は、機械学習モデルのパラメータをデータに最も適合するように調整するための基本的な手法です。多くの機械学習アルゴリズムで、この方法が根底にあり、モデルがデータから学習するプロセスを支えています。最尤推定を通じて、モデルは観測データが最も高い確率で生成されるように最適化され、予測や分類の性能を向上させます。
そして上掲のQiita投稿は、その中間で遂行される「ニューラル・ネットワーク座標系上のデータ集合をあらかじめ検定に合格する様に調整する処理」について、それぞれのデータが「ライフサイクル」上たどる経路$${R=\left[r_i\right]_{i=0}^n}$$に注目すれば、アフィン変換(すなわち平面上の移動、拡大縮小、回転)によってグラフィカルな表現が可能と指摘している訳です。
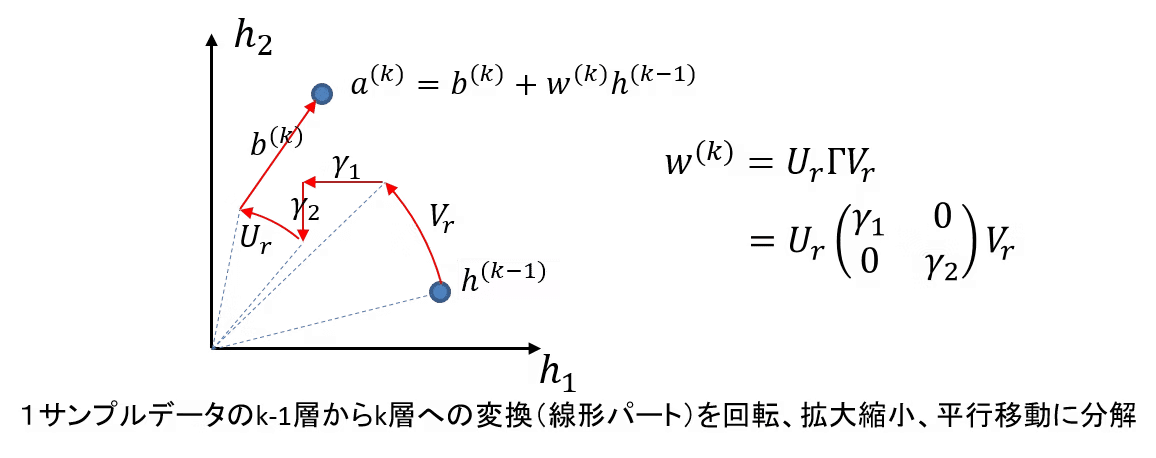

アフィン変換は二次元しか扱えないのでは?
アフィン変換(Affine transformation)は「一度に二次元しか扱えいない」方法論ではありますが、ならば何度も分けてその結果を合算すればいいだけの話で、この方法によって3次元以上の座標系にも対応する事が出来ます。
二次元アフィン変換
$$
\begin{pmatrix}
X_1 \\
Y_1 \\
1\\
\end{pmatrix}=
\begin{pmatrix}
a & b & e\\
c & d & f \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
$$
並行移動(T_x,T_y)
\begin{pmatrix}
X_1\\
Y_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & T_x \\
0 & 1 & T_y \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
$$
拡大縮小(S_x,S_y)
\begin{pmatrix}
X_1\\
Y_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
S_x & 0 & 0\\
0 & S_y & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
$$
回転(θ)
\begin{pmatrix}
X_1\\
Y_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
cos(θ) & -sin(θ) & 0 \\
sin(θ) & cos(θ) & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
$$
剪断(θ)
\begin{pmatrix}
X_1\\
Y_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0 \\
tan(θ) & 1 & 0 \\
0 & 0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
1\\
\end{pmatrix}
$$
三次元アフィン変換
$$
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
a & b & c & j\\
d & e & f & k\\
g & h & i & l \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
並行移動(T_x,T_y,T_z)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0 & T_x\\
0 & 1 & 0 & T_y\\
0 & 0 & 1 & T_z \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
拡大縮小(S_x,S_y,S_z)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
S_x & 0 & 0 & 0\\
0 & S_y & 0 & 0\\
0 & 0 & S_z & 0 \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
x軸まわりの回転(θ)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & cos(θ) & -sin(θ) & 0\\
0 & sin(θ) & cos(θ) & 0 \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
y軸まわりの回転(θ)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
cos(θ) & 0 & sin(θ) & 0\\
0 & 1 & 0 & 0\\
-sin(θ) & 0& cos(θ) & 0 \\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
$$
Z軸まわりの回転(θ)
\begin{pmatrix}
X_1\\
Y_1\\
Z_1\\
1\\
\end{pmatrix}=
\begin{pmatrix}
cos(θ) & -sin(θ) & 0 & 0\\
sin(θ) & cos(θ) & 0 & 0 \\
0 & 0 & 1 & 0\\
0 & 0 &0 & 1 \\
\end{pmatrix}
\begin{pmatrix}
X_0\\
Y_0\\
Z_0\\
1\\
\end{pmatrix}
$$
考え方がこんな風に整備されたお陰で特定分野の数学の需要が急増?
ここで紹介されてる「プログラマー向け学習カリキュラム例」においては、この程度の話「基礎の基礎」でサラッと流されてる恐るべき現実…
「N次元アフィン変換の実例」としての主成分分析(PCA)
「ニューラル・ネットワーク座標系上のn次元データ集合」をグルグル回して好きな方角から眺められるという事は「直交する視座のセットが発見出来れば正面図や上面図や側面図が起こせる」すなわち解析学でいう微分が可能になるという事です。

まさにそうやって「とりあえず計算に不要な次元」をバシバシ削除したりデータ集合の特徴量を捉えやすい視線の角度を探すのが主成分分析(Principal Component Analysis)という次第。
主成分分析(Principal Component Analysis, PCA)は、機械学習において非常に重要な手法であり、特に次元削減とデータの可視化に用いられます。以下に、PCAの基本的な概念と機械学習における役割、そして具体的な応用について説明します。
PCAの基本概念
PCAは、データの分散が最大となる方向を見つけ、その方向にデータを投影することで、データの次元を削減する手法です。以下のステップで行われます:
データの中心化:
データセットの各変数の平均を0にするために、各データポイントからその変数の平均を引きます。
共分散行列の計算:
中心化されたデータの共分散行列を計算します。
固有値分解:
共分散行列を固有値分解し、固有ベクトルと固有値を求めます。固有ベクトルは主成分の方向を示し、対応する固有値はその方向に沿った分散の大きさを示します。
次元削減:
最も大きな固有値に対応する固有ベクトルを選び、それらを用いてデータを新しい次元に投影します。
機械学習におけるPCAの役割
1. 次元削減
高次元データを低次元に変換することで、計算コストを削減し、アルゴリズムの効率を向上させます。これにより、過学習を防ぎ、モデルの一般化能力を向上させることができます。
2. データの可視化
高次元データを2次元または3次元に投影することで、データの構造やクラスターを視覚的に把握することができます。これは、探索的データ解析や結果の解釈に役立ちます。
3. 特徴選択
最も重要な特徴を選び出すことで、ノイズや冗長な情報を除去し、モデルの性能を向上させます。PCAを用いて選ばれた主成分は、元の特徴の線形結合であり、情報の損失を最小限に抑えつつ、データの本質を捉えます。
PCAの具体的な応用
1. 画像処理
画像データは高次元であることが多く、PCAを用いることで次元を削減し、計算コストを削減します。例えば、顔認識では、顔画像を低次元の主成分空間に投影することで、効率的に特徴を抽出します。
2. クラスタリング
PCAを用いてデータを低次元に変換することで、クラスタリングアルゴリズムの性能を向上させます。次元削減により、データのクラスタ構造が明確になり、クラスタリングの結果が改善されます。
3. アノマリー検知
高次元データ中の異常点を検出するために、PCAを用いてデータの次元を削減し、低次元空間での異常点を識別します。低次元空間では、正常データと異常データの分離が容易になることがあります。
機械学習アルゴリズムとの統合
1. 前処理としてのPCA
多くの機械学習アルゴリズムの前処理ステップとしてPCAを使用します。例えば、サポートベクターマシン(SVM)やk近傍法(k-NN)などのアルゴリズムでは、高次元データを低次元に削減することで、計算効率を向上させることができます。
2. パイプラインでの利用
Scikit-learnなどの機械学習ライブラリでは、PCAを他の前処理手法やアルゴリズムと組み合わせてパイプラインを構築することができます。これにより、データの標準化、PCAによる次元削減、分類器の訓練を一連のプロセスとして効率的に実行できます。
結論
主成分分析(PCA)は、機械学習において次元削減、データの可視化、特徴選択など多くの目的で利用される重要な手法です。PCAを用いることで、データの本質を捉えつつ、計算効率を向上させることができます。機械学習アルゴリズムとの統合により、より効果的なモデルの構築が可能となります。
このシリーズでは「カンブリア爆発期(5億4200万年前から5億3000万年前)に授かった視覚と視覚情報を処理する脊髄の末裔で考える事しか出来ない人類」が、その制約下において(行列演算に立脚する)線形代数や(微積分演算に立脚する)解析学を発達させてきた事について悲観的に語るディスクールを多用しますが、それはそれでこんな高みに到達し、その最新の精髄が機械学習理論という訳です。まさしく多様体的価値感の極みといえましょう。
そんな感じで以下続報…
