見出し画像

【試論「人工知能概念はいつから存在したといえそうか？」8パス目】コンピューター側を観測主体そのもの(Obsever itself)と設定した場合に浮かび上がってくる進化論？

Yasunori Matsuki

前回の投稿において「進化とは何か？」なる設問が、最低でも二つの全く異なる成分の合成によって構成されている構造が浮かび上がってきました。

  • ハーバード・スペンサーが社会進化論で触れている様な「(画一的で貧相な)単純状態から(多様で豊かな)複雑状態への不可逆的変遷」。科学技術やアルゴリズムの系統進化がこれに該当し「時代のニーズと合わなくなって参照されなくなる系統」が出たり収斂進化が起こったりはするものの、原則としてその進展自体は不可逆的である(実は収斂進化の発見は遺伝子解析技術が相応の段階に到達したここ最近で、そのせいで多くの伝統的進化系統図が見直しを迫られる展開に。人間の認識能力はそこまで「観察可能な事象」に拘束されている)。

任意の状態(Situation)はすべからく淘汰(Selection)を経て究極的には「(画一的で貧相な)単純状態(Simple Situation)」から「(多様で豊かな)な複雑状態(Complex Situation)」へと不可逆的成熟を遂げていく。

上掲「ハーバート・スペンサーの段階的発展説」

今もし夏后氏の世（夏王朝）に、巣を組み、木と木をすり合わせて火をおこす人があったとすれば、必ず鯀・禹に笑われるであろう。殷・周の世に、川の堤を切る人があったとすれば、必ず湯王・武王に笑われるであろう。してみれば当今の世に、尭・舜・湯・武・禹の道を褒めたたえる人があるとすれば、必ず新しい聖人に笑われるであろう。されば聖人は必ずしも古えに循おうとはせず、一定不変の道に法とろうとはしない。当世のことを論じて、それの備えをする。

本田済「韓非子」 全現代語訳
「葬送のフリーレン」10巻
「葬送のフリーレン」10巻
「葬送のフリーレン」10巻
「葬送のフリーレン」10巻

  • (個体の場合は細胞の集合、コロニー(群)の場合は個体の集合によって構成される)観測(Observation)の対象は、それぞれの観察単位で準安定状態(metastable state)にある必要がある。そもそもその始まりと崩壊過程と終焉を観察するのが進化論なので。

真の安定状態では無いが、大きな乱れが与えられない限り安定に存在できるような状態。準安定状態は小さな乱れに対しては安定であるが、大きな乱れが与えられると不安定になり、真の安定状態へ変化してしまう。

準安定状態は非平衡状態なので、いつかは真の安定状態へ変化するが、その変化の時間が非常に長いのが特徴である。

上掲Wikipedia「準安定状態」

酵素や生体は確かにどちらも準安定な状態にある。酵素の安定な状態とは効目のなくなる事であり、また生体の安定な状態は死ぬ事である。全ての触媒はしまいには効かなくなってしまう。触媒は反応速度を変えるものであって、真の平衡状態を変えるものではない。しかし触媒も人間もどちらも、十分はっきりした準安定状態をもつので、これらは比較的恒久性のある状態と考えてよいほどである。

ノーバート・ウィナー「サイバネティクス(1948年初版、1961年増補)」

オブジェクト思考プログラミングにおけるクラス定義(とりあえず多重時継承はなし)と、オブジェクト(プログラム動作中、実際にメモリ上に置かれ、参照数が0になるとリリースされる)の関係を彷彿とさせますね。

  • 「とりあえず多重時継承はなし」…その場合の常套手段たるClass in Classの技法が収斂進化っぽい。mixIn(インスタンス変数を継承するクラスは1つだけ、他のクラスはメソッドだけとする多重継承)技法についてどう考えるかは要検討。

  • この件、ポリモーフィズム（Polymorphism=多態性）によるパラメーターの組み合わせ拡張概念との兼ね合いも出てくるから、案外単純でない？

ただしオブジェクト思考プログラミング技法自体には「オブジェクトの振る舞いのクラス定義へのフィードバック」なる概念までは含まれていません。そのあたりはあくまでライプニッツの「(窓がない)モナド」論の様に「第一原因(神の様な超越的存在)の介入」を前提とするシステムといえましょう。そう考えるとより近いのはシルル紀(4億3800万年前~4億800万年前)に登場した珊瑚礁と珊瑚虫の関係とも？

なお前回の投稿で触れた「バイオミミクリー(Biomimicry=生物模倣)」は、この観点から整理すると「自然界に存在する多様な準安定状態の観察結果から従来の発想になかった数理を抽出して人類の知識体系に追加する」方法論に分類される様なんです？

  • しかしそもそも「自然観察から学ぶ」態度自体は物理学、ひいてはそれから分岐した数学の出発点でもあった筈。

  • こうして人類の知識体系は否応なく「局所的にしかユークリッド座標系が設定出来ない(全体を一つの直交座標系として表現する事が不可能な)多様体(manifold)」として構成される展開を余儀なくされてきた訳である。

さてここでその様な珊瑚礁(知識体系)を形成してきた珊瑚虫の生理、すなわち「生物における「快を求め、不快を避ける本能」=人工知能における「予測誤差を最小限に減らすアルゴリズム」」に注目すると…

行動がベクトル量である以上、快不快もまたスカラー量ではあり得ない。ただしここでいう特定の主体がそれをスカラー量としか感得出来ない場合ならあり得て、取り得る行動可オプションの中から「最も快を増大させ、不快を減少させる選択肢」を選び続けていると考えるなら、それは「それなりに十分に」上掲の「人工知能の予測誤差を最小限に減らすアルゴリズム」と一致する。

  • 「それぞれの観察単位において準安定状態(metastable state)の始まりと途中過程と終焉が観測される」観測主体(Observer)と観測対象(Observation Target)は、個体の場合は細胞の集合、コロニー(群)の場合は個体の集合によって構成される。集合論における「集合そのもの(Set itself)」と「元(Element)」の関係。

  • そして、かかる観測行為そのもの(Observation Itself)の連鎖を数理的に連続的に表すには、とりあえず集合論における閉世界仮説(Closed world assumption=とりあえず最外部の補集合を空集合と置く戦略)あるいは解析学における「(とりあえず外測度範囲を0に設定する)ルベール測度b-a概念」を導入して線形性、すなわち加法性 f(x + y) = f(x) + f(y)や 斉次性 (αx) = αf(x)の様な数理が通用すると想定すると何かと都合が良い。ある意味そうした「直交座標系(Cartesian Coordinate System=デカルト座標系)指向」そのものが「カンブリア爆発期(5億4200万年前~5億3000万年前)に視覚と視覚情報を処理する脊髄を授かった生物との末裔」の思考様式を拘束する「祝福」にして「呪い」といえるかもしれない。

  • 機械学習アルゴリズムなどが威力を発揮するのは単純にこう考えられない場合であり、そこに独特の準安定性が存在する。

コインを1枚投げた時のエントロピー(平均情報量)

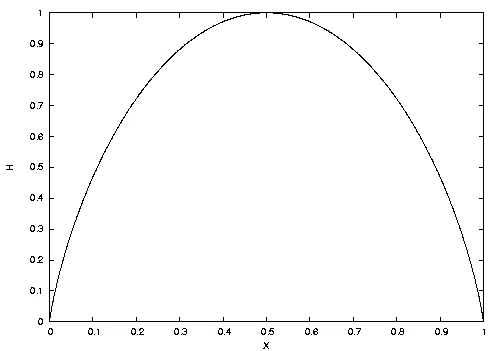
マクスウェルの魔の話と重ねると①出目が表か裏か完全に確定した情報エントロピー0の状態が「真の平衡状態(もうこれ以上の変化はもう起こらない)」。②それに対し「準平衡状態」は一応、過程としては「投げる前あるいは空中でコインが回転している状態」から含むが「観察と予測こそマクスウェルの魔の本領」と考えると、接地して跳ね回ってる(最終的な出目が揺らいでいる)状況こそが本番とも見て取れる。

機械学習アルゴリズムもまた、ここでいうマクスウェルの魔同様「観察と予測こそが本領」なのであって「出目が確定した(これ以上変化が起こらない)情報エントロピー0固定の状態」においても「状況が純粋に確率論的にしか予測不可能な(情報エントロピーを下げる手段が存在しない)情報エントロピー1固定の状態」においても出番がない。

上掲「試論「人工知能概念はいつから存在したといえそうか？」」5パス目

一周して「イタリア・ルネサンス期(14世紀-16世紀)、天文学や解剖学が飛躍的に発展したボローニャ大学やパドヴァ大学の教授や学生の間で広まった科学実証主義(Scientific Positivism)の祖型」新アリストテレス主義(Neo Aristotelianism)に戻ってきた感があります。

  • 実践知識の累積は必ずといって良いほど認識領域のパラダイムシフトを引き起こすので、短期的には伝統的認識に立脚する信仰や道徳観と衝突を引き起こす。

  • 逆を言えばどんな実践知識の累積が引き起こすパラダイムシフトも、長期的には伝統的な信仰や道徳の世界が有する適応能力に吸収されていく。

こうして①閉世界仮説においては「最外縁の補集合」として、②ルベール測度論においては「外測度問題」として切り捨てられる「(最外縁に存在しなければならない)観測主体そのもの(Observer Itself)の観点」が「進化とは何か？」なる設問を構成する第三の成分として浮上してくる訳ですね。例えばレヴィ=ストロースいうところの「二重分節（double articulation）」問題…

レヴィ=ストロースは絵画についての考察において、葛飾北斎やニコラ・プッサン（17世紀のフランスのバロック画家）の絵を例にして、そこに「二重分節（double articulation）」という構造を読み取る。簡単に言うと、これはコラージュ的な手法のことで、あらかじめ描こうとする人物や景色の断片を一つ一つ個別に描き、その後でしかるべく配置をして一つの作品に仕上げるという方法である。その結果、北斎やプッサンの絵画では、全体としても統一的な絵となっているが、その部分をみても一つの完成された絵となっている。二重分節という意味においては、第一次文節においてすでに小さな（完成された）作品があり、それらが適当に組み合わされ配列された第二次文節において、全体が高次の作品となる。

二重分節あるいはコラージュ的な配置は、文学で言えばマルセル・プルーストの『失われた時を求めて』にもみられるとレヴィ=ストロースは述べる。そこではさまざまな時系列の印象が同時に語られ配置されており、通常の小説にみられるような時間の流れとは異なっている。「物語の織り目に無意識の記憶が介入することで、出来事の継起と時間の持続のなかで、その順序を完全に変えてしまう創作の手法が補償され、均衡を維持」（上掲書, p.3）しているという。

しかし、私たちの無意識における時間の構造はむしろそのようなものであり、コラージュ的／二重分節的に配置されているのではないか。実際に、プルーストは『失われた時を求めて』を書くにあたり、異なった状況、異なった時期に書かれた草稿群を、後から満足できる順序に整理し、再構成しているという。つまり「作品を書くときに彼がおこなっているのは接合であって、たくさんの断章を互いにつなぎ合わせる」ということであった。

上掲「レヴィ=ストロースの「みる・きく・よむ」を読む」

  • この問題「任意の数に、その数をその量たらしめる乗法単位元１が存在しなければならないなら、一次元量における「乗法単位元１」は何処に存在しているのか？」なる設問が重力加速度や無次元量「傾き１」、さらには虚数概念$${i^2=e^{πi}=-1}$$に到達するのと同次元の発想といえよう。

最小二乗法概念の出発点たる「相加平均≧相乗平均の不等式」
ここから複素極座標系への拡張はほとんど自明の場合といってよい。

  • そういえば「ニュートンの運動方程式」の「ラグランジュの運動方程式」への拡張もまた(一般化座標系(Generalized Coordinate System）概念導入による)「デカルト座標系概念の呪い」からの脱却の試みであったとも？

おやおや？この三重構造「コンピューター側を観測主体そのもの(Obsever itself)と設定した場合に浮かび上がってくる進化論」に他ならないのでは？ そこまで到達した時点で以下続報…

いいなと思ったら応援しよう！