見出し画像

【数学的溢れ話15パス目】スズメバチの数え方？

Yasunori Matsuki

近所の緑地でスズメバチを見掛け、その数え方について考える様になりました。

  • 統計学上の「十分に長い単位期間」として1週間を設定。その間に平均1匹観測されるかどうかくらいだったら「近くにスズメバチの巣はない。たまたま見かけただけ」と考える。

  • 平均2匹以上観測される様だったら「やれやれ、どうやら近くにスズメバチの巣がある様だ」、5匹~10匹観測される様だったら「高確率で緑地内にスズメバチの巣がある。駆除の必要があるかもしれない」と考える。

念頭に置いたのは指数分布とポアソン分布。想定出現率λは上掲の最低条件設定から1匹を下回らないものとし(λ≧1)、その一方で実際の観測数xは0匹もあると考えます(x≧0)。

$$
指数分布Exp(x;λ)=λe^{-λx}(λ≧1,x≧0)
$$

$$
ポアソン分布Po(x;λ)=\frac{e^{-λ}λ^x}{x!}(λ≧1,x≧0)
$$

なお、ここでいう「十分に長い単位期間」は、とりあえず以下の考え方に従って「1秒に対する1分(60倍)」あるいは「1分にたいする1時間(60倍)」くらいの頻度と想定しています。

具体的計算過程は以下。

  • 指数分布にとって観測匹数が増えるのは(正多角形の頂点数が増える様に)その数だけ単位区間を区切られるのと同じ事。確率分布もその範囲に圧縮された様な感じに。なお観測数0匹の場合はベイズ統計学における「理由不十分の原理」に従った確率均等割りを遂行しております。

  • ここに登場する「ベイズ統計学における理由不十分の原理に従った確率均等割り」は一様分布の考え方そのもので「何匹までを現実ラインと考えるか？」によって割り振り確率が揺らぐ。ベイズ統計学では、この「事前分布」は「事後分布」の想定現実ラインに合わせて調整する。

  • その一方でポアソン分布は観測匹数が増えるほど正規分布に近づきます。

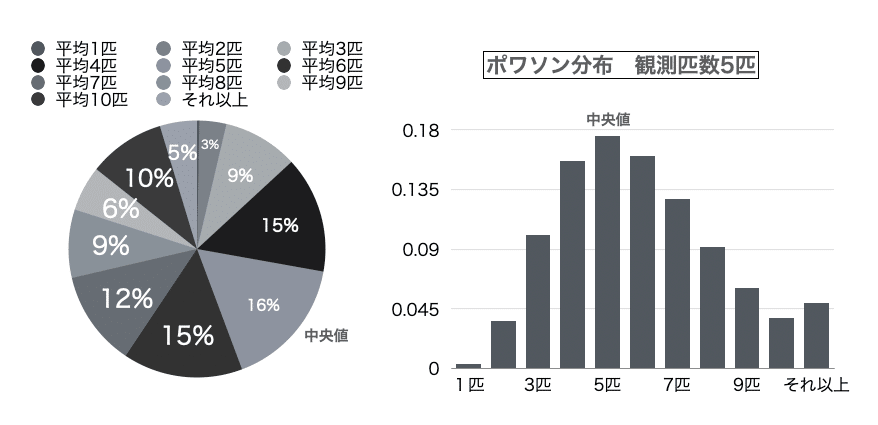
この観測匹数が増えるにつれどんどん想定分布の分布が変貌していく様子、がっつりベイズ更新そのもの。特に「１匹も観測されてない時」と「1匹だけ観測された場合」で分布が変わってくる辺りが「主観確率」概念そのものという。

なおここまでの分析、頻度主義では「自明の場合として、データ不足により吟味不可能(笑)」と一蹴されてしまう範囲で、判断に何のヒントも与えてくれません。それに対し、しばしば人度主義側から「社長決済尺度(ただの直感に過ぎず、数学の対象たる条件を備えてない)」と悪態を吐かれてきたベイズ主義は、しばしばそういう状況下でそれなりの判断を下さざるを得ない現実の生活者たる我々の為に必然性を帯びて登場した考え方で、その意味合いにおいて昨今の人工知能ブームの大源流の一つといえましょう。

観測匹数による「いる」「いない」情報のエントロピー推移

分布全体が正規分布に近づくにつれて情報エントロピーが0に漸近していく感じもまた興味深いところ。その出発点を以下と置くと、その平均情報量(情報エントロピー)は以下の様に推移します。

$$
H(P)=-\sum_{i=1}^nP_ip \log_eP'_i=-\frac{1}{2}\log_e \frac{1}{e}-\frac{1}{2}\log_e \frac{1}{e}=\frac{1}{2}+\frac{1}{2}=1
$$

  • あれ？単調減少じゃなさそうな箇所が…計算ミス？それともガンマ関数の仕様？

階乗n!は0!と1!の値が等しく1となるが、ガンマ関数ではΓ(n+1)となるのでこれが1から2の区間に対応。

なるほど我々がスズメバチの観測数が増えるにつれ「こりゃ近くに巣があるな」と確信を高めていく過程はこの様に数理的には①(コインの出目が確定する過程の様に)情報エントロピー全体が0=「自明の場合」に向かう過程で②「いない」情報のエントロピーが相対的に1に近付く「絶地天通プロセス」として観測される訳です。そしてそれは頻度主義における棄却検定過程において「いない」なる対立仮説が棄却されていく過程そのものであり、その結果として「いる」の正しい在り方たる正規分布が視界を被覆するという次第。

「平均１匹」と「平均2匹」の挟間(β関数を用いた数え方)

β分布Be(x;α,β)を用いると、以下の様な数え方も出来る様です。

  • まずススメバチの観測データを「必ず各区画の観測数が1か0になる」様に均等割する。

  • α=観測成功数(観測数1の区画数)、β=観測失敗数(観測数0の区画数)としてβ分布Be(1+α,1+β)を求める。

  • あらかじめ定めた観測成功率(例えばβ分布Be(1+α,1+β)≧0.8)を上回った状態であらかじめ定めた観測間隔(例えば1日)を下回る様なら「スズメバチはいる」と考える。

この考え方はそのまま「ゴ○ブリの数え方」に応用出来そうだ？　そんな感じで以下続報…


この記事が気に入ったらサポートをしてみませんか？