
【対陣地戦用弾薬庫】初心に帰る。
実は私がこのnoteに引っ越してきたのは忘れもしない2023年9月27日、以下に述べる様な連中の襲撃を受けXアカウントを凍結に追い込まれたのが契機だったのです。
気のせいかな?①昨年9月27日に数時間に渡るネットリンチの末に私のアカを凍結に追い込んだ連中は、まさにこういう感じだった。②1年振りに復活してみたら、現在のツイフェミにはもはや往年の動員力は残っていない様で、その一方同様の騒ぎが反AI陣営で起こっている。もしかして引っ越した? https://t.co/Eruiy23jvn
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
ネットリンチで凍結に追い込まれるまで随分と時間があったのでじっくり観察出来たけど①扇動役を担う中間アカ集団が存在し、日本共産党とかれいわ新撰組みたいに「即時社会全体を変えねば‼︎」と叫ぶ急進政党の熱烈な支持者が比較的多いが、左翼どころか私が(あえて)カール・マルクスを引用しまくると…
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
https://x.com/YazMatsuki/status/1850374515014140367

で、そういう連中はソシャゲの微エロ画像とか集めてる事が多く(tumbrでもそうだったが、ガチにDSM定義レベルのパラフィリアすら混ざってた。「木を隠すなら森の中」ってやつ)、その辺りが反AI陣営への転身と関わってくるのかも。https://t.co/5CTHSg0aVw
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
そういうアカウントはあくまで扇動投稿の大元を辿った時、その交差点として現れるだけで全体に占める割合はごく僅か。さらにいうと、たまたまその時私を襲った扇動元の一つがそういう連中だっただけで、他にも多数のタイプが存在する可能性も。まぁこの辺りはあくまで「サンプル1」なので。
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
実際、この様な集団を成立させているのは恐ろしいまでの相互無関心。tumbrでの経験では、例えばアメリカでは(BLM運動を暴動化したり、略奪を扇動して喜んでいた)無政府主義者(ANARCHIST)が暗躍するケースが多く、擬装もより徹底しておりそこまで辿り着けないケースの方が大半でした。
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
こうした連中の集団としての特徴は①(まるで捕食動物の様に)定期的にネットリンチにかけられる獲物が補充され続けないとあっけなく霧散するか内ゲバで滅ぶ。②ただしメモリレスなので幾度でも蘇って来る(その都度怒りをぶつける相手が微調整される)。
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
③この様な「色即是空空即是色」な存在の存続率は純粋に「アウトレンジでネットリンチにかけられて、相手の反撃は絶対に自分に届かない様な絶対弱者を絶えず供給し続けてくれる絶対正義の確度」に依存。https://t.co/vCMSVOl9YR
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
で、その様な扇動の成立に欠かせないゴブリンリーダー(仮名)を魅了して集めるのに欠かせない「確度」が、既にツイフェミには存在せず反AI陣営がそれを代替する様になったのではないかと推測した次第。なお「代替わり」する前の「正義」は概ねこんな感じ。https://t.co/yjWHtAzlTo
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
なお「扇動される有象無象側の心理」についてはこちらの「闇バイトに動員される連中の心理分析」に共感を覚えます。 https://t.co/LkacA37I4U
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
あくまで「ナチスそのもの」でなく「常備軍の数倍の規模に達してナチスによる政権奪取に利用された後に粛清され消滅したSA(突撃隊)」、あるいは…https://t.co/LGdLW1vvJm
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
「文革そのもの」でなく「毛沢東に利用されたた挙句、その反逆精神が最終勝者たる毛沢東に向く前に下放によって強制解散させられた紅衛兵」という認識で、その伝統的心理構造が昨今の「闇バイト問題」とも重なって来る辺りが重要かと。https://t.co/mBw8pZX88p
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
この様な生態はダーウィンによる種の定義「確率論的かつ系統的に推移する準安定状態」どころか、その下位互換たるサイバネティクス研究対象の定義「多種多様なフィードバックによって準安定状態を保ち続ける系」の条件すら満たしていませんが…https://t.co/dkmwWF9I3m
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
それは準安定性、すなわち回路方程式でいう「定常状態」を維持したままの推移にこだわるからで、この問題はその外側にさらに「リセットさん=終了処理(最終遷移状態)が訪れる都度、必要なデバッグを加えた上で上でまた初期化処理(初回遷移状態)を遂行してくれる主体」を想定すれば解決します。 pic.twitter.com/rrg65qXfQb
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
これ「自らをプログラミングし続けるプログラム」すなわちAGI(Artificial General Intelligence=汎用人工知能)の実現方法の一つなんですが、という事はかかるゴブリン集団こそが史上初めて現れた(生体素子を組み込んだ形での)AGIという事に?そんな感じで以下続報… pic.twitter.com/r37pDFctcY
— Yasunori Matsuki (@YazMatsuki) October 27, 2024
とりあえず、そんな感じで以下続報…
【旧投稿】「パスを切る」概念自体の定義
コーシーの積分定理(Cauchy's integral theorem)によれば、正則である複素関数の積分結果は0となります。
そして正則(regular)であるとは、多角形の辺長が全て同じだったり、(全)微分可能である状態を意味します。
単純化して考えてみましょう。
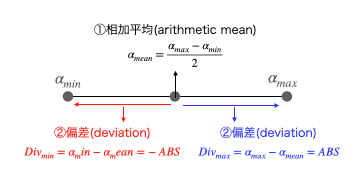
まずは任意の二点を直線で結び、その線に沿った距離の相加平均(arithmetic mean)を求める。
これを使って偏差(deviation)を取ると絶対値(absolute value)が同じで符号だけ逆の2つの値が得られる。
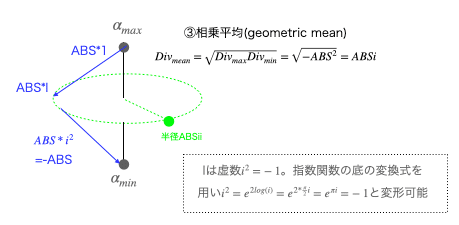
その相乗平均(geometric mean)を求めるとあら不思議。こんな単純計算なのに虚数が?
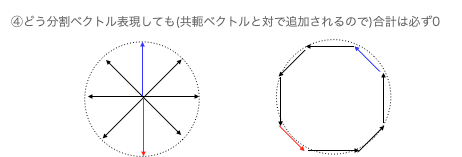
そしてここに現れた複素閉曲線(虚数円)は「中心から円弧まで垂線を伸ばしたベクトルの合計」を求めても「円弧上を均等割したベクトルの合計」を求めても必ず答えが0となる。
この意味合いにおいて「(全)微分が取れる」と「多角形の辺長が全て同じ」は重なる訳で、要するに「同じ演算の連続だけで全体が規定可能な構造」が相似しているといえましょう。
でも一般に(グラフ理論の出発点である)経路問題は閉曲線である事(すなわち出発点と終点が同じ事)を想定してないのでは?ここでは(有限周期のみを扱う)フーリエ級数を(無限周期が扱える)フーリエ変換に拡大する際の方便、すなわち「-♾️を始点、終点を+無限とする開直線、あるいは0を始点、♾️を終点とする半開直線はある種の閉曲線と見做せる」という考え方を採用。
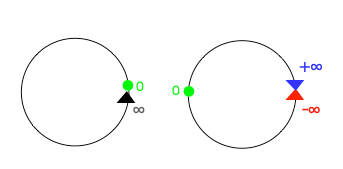
ここではこの様な領域の取り方を「パス(閉曲線)を取る」と呼ぶ事にしますが、実際にはその投稿が想定する/しない次元の考え方の宣言列に。
そんな感じで以下続報…
