
カイ2乗検定で比率の差を検定
東京大学医学部老年病科の矢可部です。
基礎、臨床研究の統計解析でRを用いています。
学生や研修医の指導に使うという目的もあり、noteに記事を書いています。
今回は、群間での比率の差を検定するカイ2乗検定のやり方を解説します。
2群でのカイ2乗検定
例題1
ある外来に通院中の患者全員について、フレイル(注)か健常かを判定した。
フレイルと判定されたのは男性17人と女性21人で、健常と判定されたのは男性86人と女性99人であった。
フレイルと健常で男女比率に差があるか、有意水準5%で検定せよ。
(注: 身体機能は自立しているが、加齢の影響で複数の臓器の予備能が低下し要介護状態に陥るリスクが高い状態をいう)
クロス集計表を作ると以下の通りです。

Rに表形式のデータを取り込むには、以下のように入力します。
# 2×2のクロス集計表を作成し、datという名前で保存
dat <- matrix(c(17,86,21,99),2,2)
ここで"2, 2"とありますが、1つ目が行数、2つ目が列数です。
列ごとに(縦方向に)数字を入れていくことに注意してください。
作成したdatを表示すると、2×2の形で正しくできていることがわかります。

カイ2乗検定を行う場合、以下のように入力します。
# datでカイ2乗検定 (イエーツの連続性補正は行わない)
chisq.test(dat,correct=F)
結果は以下のように表示されます。

P値が0.05を超えているので、「男女比率に有意差はない」という結果になりました。
なお、上で出てくるイエーツの連続性補正の説明はここでは割愛します。
詳しい説明、どのような場合に行うかなどについては、以下のサイトなどをご覧ください。
3群以上でのカイ2乗検定
カイ2乗検定は3群以上でもできます。ただし、少し工夫が必要です。
例題2
クリニックA, B, C の定期受診患者数を男女別に調べたところ以下の通りであった。
A: 男性86人、女性76人
B: 男性68人、女性165人
C: 男性65人、女性76人
クリニックA, B, C間で男女比率に有意差があるか、有意水準5%で検定せよ。
クロス集計表は以下の通りです。
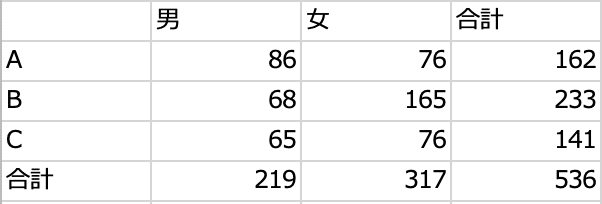
まず、表を作成します。
# 3×2のクロス集計表を作成し、dat2という名前で保存
dat2 <- matrix(c(86, 68, 65, 76, 165, 76),3,2)
dat2を表示すると以下のようになります。

カイ2乗検定を行うコマンドは、基本的に2群の場合と変わりありません。
# dat2でカイ2乗検定 (イエーツの連続性補正は行わない)
chisq.test(dat2,correct=F)

P値が0.05より低いので、「3群間で男女比率に有意差がある」という結果になりました。
ただしこれだけでは、どの2群間に有意差があるかはわかりません。そこで、2群ごとにカイ2乗検定を行います。
AとB, AとC, BとCのそれぞれでカイ2乗検定を行うと、以下の結果が得られます。

注意点として、ここでは検定の多重性が問題となります。
同じデータに対して3回の検定を繰り返しているため、有意水準が0.05のままだと有意差が出る確率が上がってしまいます。
そのためボンフェローニ法を用います。これは有意水準を総検定数で割った数値を基準にするというものです。
今回は有意水準0.05を3で割り、
0.05 ÷ 3 ≒ 0.0167
より、p < 0.0167であれば有意差ありと判定します。
例題2では、AとB, BとCでは割合に有意差があり、AとCには有意差がないという結果になります。
今回は以上です。
