
理科 単元「じしゃくのふしぎ」×算数カード実践
はじめに
算数でカード実践を行っていると、そのカードが漢字の宿題に転移していたり、他の教科も使われることがたまに見られる。
今週は算数で使っているカードが理科で使われ、学びを驚くほど深めていた。
自由進度学習で授業を進めているため、授業の進度は個々で異なるため、今回は、ある2つのグループ(グループでやっているわけではない)の学びの深まりについて書いていく。
グループ①
実験内容
本時の学習では、磁石に釘をつけ、その釘をクリップに近づけるとクリップがひっついてくるとことから、
磁石の力が釘の先端まで届いてる
のではないかと考えていた。
また、釘を2本にするとひっつくクリップが減ってしまうことから、
釘を2本にしたことで先端までの距離が長くなったことで伝わる磁石の力が弱くなったため
と考えていた。

ここまでは理科ノートにある内容である。
算数とのかけ算スタート
算数みたいに数を増やそう!釘を反対に増やしたらどうなるかな?

きっと、この発言は興味的なものであったと思う。しかし、この疑問が学びを深めていくことになる。
子どもたちは、
N極の釘によって磁石が反対にも長くなってるから…
分からない。
予想ができたない。
と予想が立てにくそうだった。しかし、気になる子どもたちは、実験を行ってみた。すると、クリップがつく、つかないの問題以前にN極に釘をつけるとS極の2本目の釘が落ちてしまうのである。

これに対し、何で?何で?と疑問が疑問を生んでいた。そのとき、
算数のベツアラワシ(図に置き換えるというカード実践のカード)使ったら分かるかも
と言いだし、班で話し合い、以下のものをロイロノートの提出箱へ入れていた。

これは、はじめ磁石というのは、N極S極に5つのNの力やSの力を持っていると仮定したところから、この図がスタートしている。
左側の実験では、釘を2個つけると、S極側の釘の先端のほうにSの磁石の力が移動する。この磁石のSの力を引き付けるために、N極の3つのNの磁石の力が働いていると考察した。
さらに右側の実験では、N極に釘がつき、磁石のN極の中のNの力が1つとなり、このN の力1つではS極の2つ目の釘を引きつけることができなかったのではないかと考察した。
グループ②
グループ②では、理科の実験内容が全て終わり、最後に磁石の力を使っておもちゃを作るということを行っていた。その時、磁石の反発する力を使っておもちゃを作ろうとしていたものの、想定外のことが起きたようだった。その想定外の事とはN極とN極がくっついてしまうというハプニングであった。

そこからその子たちの探究が始まった。
実験内容
このハプニングから磁石の力には、向きがあるのではないか。またあるとしたらその向きはどのような向きなのか調べるという実験であった。
この実験は図のように、実際に磁石と磁石をくっつけて、その体感した反発を◎、〇、△で記録するというものであった。(下の資料は、実験方法と実験から得られた結果と分かったことが示されたものである。)
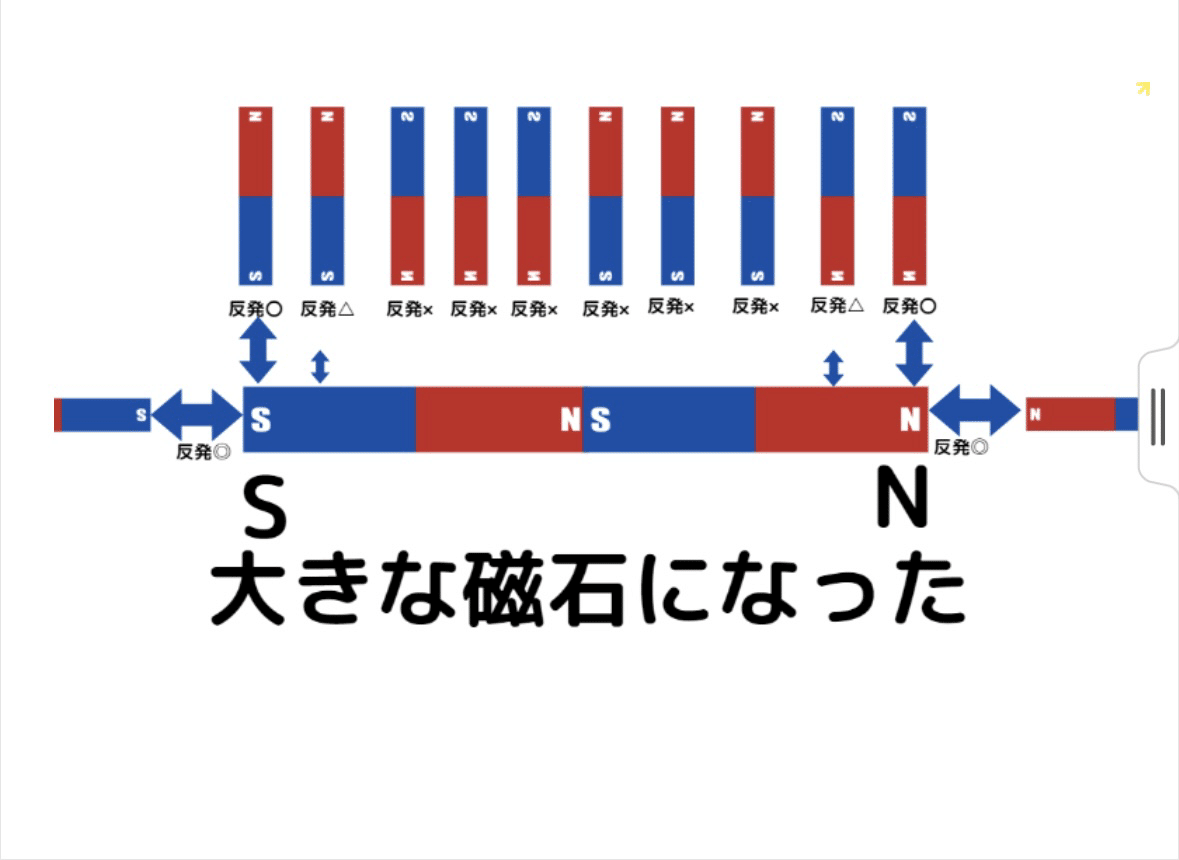
算数とかけ算スタート
上記のように、実験結果からわかったことをまとめると
1つ分に着目して考える
という算数のカードを取り出し、磁石が2つで1つの大きな磁石となっているが、これが磁石1つだった場合には、同じ現象が起こるのか考えるというものであった。
その結果、磁石1つだと、N極とN極はどの部分であっても反発を感じるという結果が生まれた。
ここから子供たちは、ひとまずの考察として、以下のようにベツアラワシ使って書き始めた。



子供たちの考えと考察は、磁石が2つあると、磁石同士を引き合わせなければならないため、S極とN極はまっすぐお互いを引きつけ合っているのではないか。
つまり、2つの磁石を引きつけ合うために、持っている磁力が縦方向ではなく横方向のみに働くことでN極とN極もくっつくのではないかと考えることができた。
まだ疑問が残る子供たち
自分たちで上記のように考察することができたものの、まだ子供たちの中には疑問が残っている様子だった。
すると、算数でいつでもカードが使えるか試しているみたいに1つ分をまた変えてさっきと同じ実験をしたらいいんじゃないと言い始めた。これは以下のような実験を考えるものだった。
1つの磁石を割ることによって、1つ分の大きさをさらに小さくし、初めに行った2つの磁石をくっつける実験と同じ現象が起こるのかと再現性に着目したものであった。
来週は、棒磁石を割るという前代未聞の実験が始まる。どうなるのだろうか。

結果
実際に2本の棒磁石を折って実験をしてみたすると折ったN極とN極が引きつけあったのである。

これを見て、子供たちは
NとNがくっついたと
びっくりしていた。
この後、子供たちは他の場合だったらどうなるのだろうかと考え、S極とN極を近づけてみた。すると、普段なら引きつけ合うものが退けあっていたのである。

この結果から、子供たちは棒磁石を折ると、また新たにできた棒磁石の断片も、S極とN極になるということを発見したのだった。

はじめ、子供たちは、棒磁石の先端には、大きな〇極の力が働きN極S極の境目にかけて、その磁力が弱まると考えていた。しかし、実は、N極側はN極の成分だけでなくS極の成分もあり、濃度があるだけでないかと結論付けた。
