1○1×の戦略について その2
10月28日に、「1○1×の戦略について」という記事を公開した。
ここでは、ボタンを押したタイミングで読まれた文字数割合に比例して正答率が上がる、というモデルに基づいて、1対1での1○1×の対戦戦略を考えた。が、実際には正解率は文字数割合に比例するというよりは、ある「確定ポイント」を境に大きく変わる、と言われている。今回はこの「確定ポイント」を考慮したモデルで1○1×の対戦戦略について考えてみたい。
まず、問題文には1つの「確定ポイント」があり、プレイヤーはそれより前で押した場合は正解できず、それより後で押した場合は一定の確率で正解できるとする。プレイヤーA、Bは、各問題に対して「確定ポイントで押す」「押さない」の2種類の選択を行うとする。どちらか一方のみが押した場合は押した人に解答権が与えられ、AとB両方が押した場合は1/2の確率でA、Bどちらかに解答権が与えられるとする。どちらも押さなかった場合は、スルーとなって同じ条件で次の問題に進み、決着が付くまで繰り返されるとする。

プレイヤーAが解答権を得た時に正解できる確率を$${a\;(0 < a\leq1)}$$、プレイヤーBが解答権を得た時に正解できる確率を$${b\;(0 < b\leq1)}$$とする。1○1×なので、どちらかが正解すれば正解した方の勝ち、誤答すればその相手方の勝ちとする。
プレイヤーA、Bは、それぞれ$${x\;(0 < x < 1)}$$、$${y\;(0 < y < 1)}$$の割合でボタンを押す混合戦略を取ると仮定して、両者が最善を尽くしたときのナッシュ均衡を考えたい。
$${(x, y)}$$の混合戦略に対して、プレイヤーAが勝利する確率を$${p_A(x,y)}$$、プレイヤーBが勝利する確率を$${p_B(x,y)}$$とする。このゲームはスルーの際に無限に繰り返すとすれば最終的にどちらかが勝利することになるので、$${p_A+p_B=1}$$となる。
$${a}$$と$${b}$$を用いて$${p_A(x,y),\;p_B(x,y)}$$を具体的に計算すると以下のようになる:
$$
p_A(x, y) = xy\left(\frac{1}{2}a+\frac{1}{2}(1-b)\right) + x(1-y)a + (1-x)y(1-b) + (1-x)(1-y)p_A(x,y) \\
p_B(x, y) = xy\left(\frac{1}{2}(1-a)+\frac{1}{2}b\right) + x(1-y)(1-a) + (1-x)yb + (1-x)(1-y)p_B(x,y)
$$
$${p_A(x,y)}$$と$${p_B(x,y)}$$をそれぞれ左辺に移行して整理すると、
$$
p_A(x, y)(x+y-xy) = ax + (1-b)y - xy\left(\frac{1}{2}a+\frac{1}{2}(1-b)\right)\\
p_B(x, y)(x+y-xy) = (1-a)x + by - xy\left(\frac{1}{2}(1-a)+\frac{1}{2}b\right)
$$
となる。
混合戦略を取る際の非協力ゲームのナッシュ均衡は、$${(p_A, p_B) = (x,y)}$$となる不動点になることが知られている。ここで、$${p_A+p_B=1}$$であるので、不動点$${x_f, y_f}$$においては$${x_f+y_f=1}$$が成り立つ。
上の$${p_A(x,y)}$$の式から$${p_B(x,y)}$$の式を引いて、$${p_A=x,\;p_b=y}$$を代入すると、
$$
\begin{aligned}
(x-y)(x+y-xy) &= -(1-2a)x + (1-2b)y - (a-b)xy \\
&= -(x-y) + 2(ax-by) - (a-b)xy
\end{aligned}
$$
$${p_A+p_B=x+y=1}$$なので、
$$
\begin{aligned}
(x-y)(1-xy) &= -(x-y) + 2(ax-by) - (a-b)xy \\
(x-y)(2-xy) &= 2(ax-by) - (a-b)xy \\
(2x-1)(2-x+x^2) &= 2(ax-b+bx) - (a-b)(x-x^2)
\end{aligned}
$$
展開して整理すると、以下の3次方程式の形になる:
$$
2x^3 - (3+a-b) x^2 + (5-a-3b) x - 2(1-b) = 0
$$
この方程式はカルダノの方法により代数的に解くことができる。Wolfram Alphaに入れて解かせると、1つの解として以下のようなものが得られた:

この結果を、$${a}$$と$${b}$$の値を変化させてプロットすると、下図のようになる:
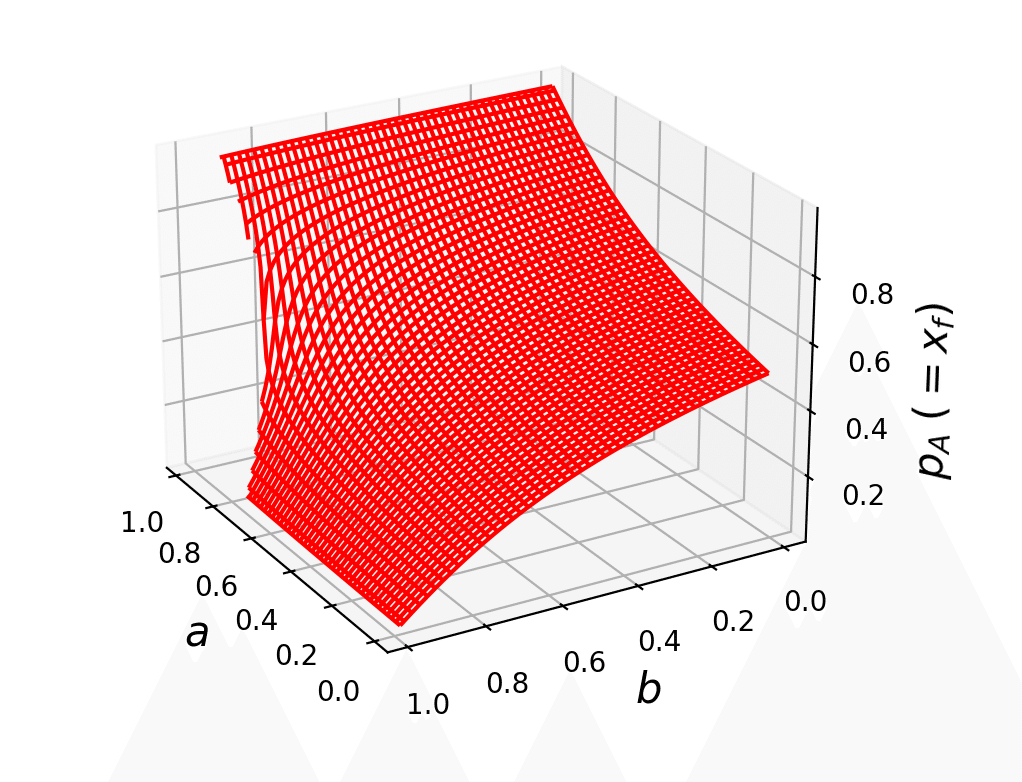

ざっくり傾向をまとめると以下のようになっている:
$${1\approx a > b \approx 0}$$のとき、$${p_A = x_f \approx 1}$$
$${1\approx b > a \approx 0}$$のとき、$${p_A = x_f \approx 0}$$
$${1\gg a \approx b \approx 0}$$のとき、$${p_A = x_f \approx 0.5}$$
$${1\approx a > b \gg 0}$$のとき、$${p_A = x_f \approx 1}$$
$${1\approx b > a \gg 0}$$のとき、$${p_A = x_f \approx 0}$$
ナッシュ均衡がこういう傾向を示すというのを、それぞれ理由付けして考えてみる。
$${1\approx a > b \approx 0}$$のとき、つまりプレイヤーAがプレイヤーBより圧倒的に強いとき、Aとしては基本的に押し勝って正解するのが良い。押さない場合はその分プレイヤーBにチャンスを与えることになる。逆にBの立場では、解答権を得てしまうと誤答失格負けのリスクが大きい。なので、プレイヤーAは1に近い割合で押し、Bは0に近い割合になると考えられる。$${1\approx b > a \approx 0}$$のときは、これとちょうど逆の形になる。
$${1\gg a \approx b \approx 0}$$のとき、プレイヤーAもプレイヤーBも解答権を得た場合の正解率が低い、つまり誤答失格負けのリスクが大きい。したがってどちらのプレイヤーも基本的には消極的な立ち振る舞いになる。
$${1\approx a > b \gg 0}$$のとき、お互いに「押し勝てば勝利する可能性が高い」状況にある。これは逆に言えば、「押し負ければ負けるリスクが高い」とも言える。プレイヤーAの方がBよりも正解率が若干高いという状況において、プレイヤーBの立場では、プレイヤーAと同程度の押し勝負をすると正解率の分で分が悪い。なので、プレイヤーBはいかにプレイヤーAの押す割合を下げさせるか、という方向性の戦略を取ることになる。プレイヤーBの押す割合が高い場合、押し負けリスクを考慮するとプレイヤーAは押す割合を上げざるを得ない。なので、プレイヤーAの押す割合を下げさせるために、プレイヤーBは自身の押す割合を下げることになる。$${1\approx b > a \gg 0}$$のときはこの逆パターンになる。
ナッシュ均衡は、あくまでお互いにお互いを読み合ってどちらも最適戦略を取ると仮定した場合の話になる。実際の対戦では、必ずしもプレイヤーは最適戦略を取るとは限らないので、必ずしもこの混合戦略の押しパターンそのままになるとは限らない。