
ワンランク上の人材選抜 人物試験におけるジレンマ(2)
「人物試験におけるジレンマ」を中心テーマにとりあげて、考察してきましたが、今回はその2回目になります。
前回(人物試験におけるジレンマ(その1))で、試験官を増やしたり面接回数を増やすことが、評価誤差を最小化する方法の一つであることが分かりましたが、では、実際に面接官を増やすと、誤差はどの程度低減していくのかなどについて、「数値モデル」を使って考えていきたいと思います。(Mr.モグ)
人物試験における数値モデルの検討
多くの採用試験では、それぞれの組織の採用目的に合った「優秀な人物」を選び出すために人物試験(面接試験)が行われていますが、他方で、人物試験には、評価者(試験官)の主観による評価バイアスが入り込む余地があることが知られています。
このバイアスを少なくするための方策について、「試験官の人数」と「評価誤差」の関係を、次のような数値モデルを用いて検討してみましょう。
「数値モデル」の前提
ここで考える「数値モデル」は次のようなものとします。
人物試験において、試験官は独立して評価するが、その際、評価を見誤ってしまう確率を「評価誤差確率(=p)」とし、p=1/10(=0.1)として分析する。
(すなわち、「採用すべき受験者」を「採用すべきでない(無能な)受験者」と見誤ったり、「採用すべきでない受験者」を「採用すべき受験者」と見誤ってしまう確率(評価誤差確率」p=1/10)は、受験者10人に1人を「見誤ってしまう」とするものです。)
わかりやすいように、次の2つのパターンについて検討してみることにします。
1 試験官人数と評価誤差の関係(各試験官の多数決で採用する場合)
受験者1人に対して、試験官1人による面接、
受験者1人に対して、試験官2人による面接
といった具合に、試験官が増えていくときの「評価誤差」の変化について検討していきます。
ただし、複数の試験官による面接が行われた場合の最終評価は、各試験官の評価の多数決で決まると仮定します※。
※通常は、試験官どうしの話合い等で議論の上、最終評価が決まることが多いのですが、簡易なモデル化を図るために多数決で決まるとしています。
(この場合、試験官の人数が偶数のときは、多数決で決められないので、確率50%で、どちらかの評価に決まると仮定します。)
2 人物試験の段階(ステップ)数と評価誤差の関係(各段階でパスした者を採用する場合)
人物試験においては、何回も面接が行われ、それぞれの段階(ステップ)をパスした者が最後に残るタイプの選抜が行われる場合があります。
例えば、最初の面接でパスした者のみが次の面接に進み、そこでもパスした者のみが最終面接に進み、そこでパスした者が採用されるというものです。
では、数値モデルを使って、具体的な検討をしていきましょう。
1 試験官人数と評価誤差の関係(各試験官の多数決で採用する場合)
○試験官が1人のケース
試験官が1人で受験者を面接するとき、前提条件から、「採用すべき受験者」を「採用すべきでない(無能な)受験者」と見誤ったり、「採用すべきでない受験者」を「採用すべき受験者」と見誤ってしまう確率(評価誤差確率(=p))は、1/10(=0.1)となります。
(すなわち、面接受験者10人に1人を見誤ってしまうことになります。)
他方、本来の受験者を正しく評価する確率は、1ーp(=1ー0.1)=9/10(=0.9)となります。
○試験官が2人のケース
試験官が2人で(1人の)受験者を面接するとき、その評価の誤差については、次の表のように場合分けができます※
※表では、「(見誤らずに)正しく評価」を「正○」とし、「見誤った評価」を「誤×」と表記してあります。
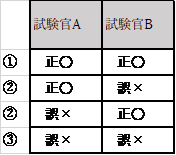
①2人とも正しく評価をする場合
この場合の確率は、9/10×9/10=0.81となります。
②1人が見誤る場合
この場合の確率は、9/10×1/10=0.09が2通りとなり、その際、(試験官が偶数で)多数決で決められないので、仮定により50%確率でどちらかに決まるとしているため、0.09×2通り×0.5=0.09となります。
③2人とも見誤る場合
この場合の確率は、1/10×1/10=0.01となります。
このように試験官が2人の場合、最終的に、「見誤る」のは、表の②③の場合なので、評価誤差確率は0.09+0.01=0.1となります。
この結果は、試験官が1人の場合と同じ結果となっており、試験官が1人から2人に増えても、(話合いによる調整がなされないのであれば)評価誤差確率は小さくならないことがわかります。
○試験官が3人のケース
試験官が3人で(1人の)受験者を面接するとき、その評価の誤差については、次の表のように場合分けができます。

①3人とも正しく評価をする場合
この場合の確率は、9/10×9/10×9/10=0.729となります。
②1人のみが見誤る場合
この場合の確率は、9/10×9/10×1/10=0.081が3通りあり、その際、多数決で「正しい評価」に決まるため、0.081×3通り=0.243となります。
③2人が見誤る場合
この場合の確率は、9/10×1/10×1/10=0.009が3通りで、その際、多数決で「見誤った評価」に決まるため、0.009×3通り=0.027となります。
④3人とも見誤る場合
この場合の確率は、1/10×1/10×1/10=0.001となります。
このように試験官が3人の場合、最終的に、「見誤る」のは、③④の場合なので、評価誤差確率は0.027+0.001=0.028となることがわかります。
このことから、試験官が2人から3人に増えることにより、評価誤差確率は0.1→0.028へと大幅に改善されることがわかります。
○試験官が4人のケース
試験官が4人で(1人の)受験者を面接するとき、その評価の誤差については、次の表のように場合分けができます。

①4人とも正しく評価をする場合
この場合の確率は、9/10×9/10×9/10×9/10=0.6561となります。
②1人のみが見誤る場合(3人が正しい場合)
この場合の確率は、9/10×9/10×9/10×1/10=0.0729が4通りで、その際、多数決で正しい評価に決まるため、0.0729×4通り=0.2916となります。
③2人が見誤る場合
この場合の確率は、9/10×9/10×1/10×1/10=0.0081 が6通りで、その際、多数決で決められないので、仮定により50%確率でどちらかに決めることになるため、0.0081×6通り×0.5 =0.0243となります。
④3人が見誤る場合(1人のみが正しい場合)
この場合の確率は、1/10×1/10×1/10×9/10=0.009が4通りで、その際、多数決で「見誤った評価」に決まるため、0.009×4通り=0.0036となります。
⑤4人とも見誤る場合
この場合の確率は、1/10×1/10×1/10×1/10=0.0001となります。
このように試験官が4人の場合、最終的に、「見誤る」のは、③④⑤の場合なので、評価誤差確率は0.028=0.0243+0.0036+0.0001となります。
これまでのことをまとめると、「試験官の人数」と「(最終評価の)評価誤差確率」の関係は次の表のようになります。

すなわち、試験官の人数を増やせば、評価誤差確率が単純に減っていく訳ではないのです。効率性の観点から言えば試験官3人で行う方が、コストの割に高い成果が得られると考えることができます。
(試験官1人から2人に増やしても、評価誤差確率は0.1で変化が無いのですが、試験官を3人に増やすと評価誤差確率は0.028に変化して効果が現れます。
他方、試験官が3人から4人に増えても、(話合いによる調整がなされないのであれば)評価誤差確率(いずれも0.028であり)は小さくならならず、効果がないことが分かります。)
今回も最後までお読みいただきありがとうございます。
次回は、人物試験の段階(ステップ数)と評価誤差の関係について、数値モデルを使って検討していきたいと思います。 (Mr.モグ)
