
人材選抜におけるジレンマ(二種類の過ち)(2)
前回から「人材選抜におけるジレンマ」をテーマにとりあげて考察してきましたが、今回は、実際の能力と試験(テスト)の成績との関係について考えていきたいと思います。(Mr.モグ)
実際の能力と試験(テスト)成績との関係
試験によって選抜を行う場合、選抜対象者(受験者)の能力と試験成績が、高い相関関係にあることが望まれます。
すなわち、理想的には、「試験の成績」と「実際の能力」が線形(比例関係を示す直線)で表現される(試験の成績が良ければ、それに合わせて実際の能力も高い)ことが望ましいのですが(上図)、実際には下図のように試験の成績と実際の能力の散布図を描くと、直線ではなく楕円形になることが知られています※。
※実際の散布図は、楕円形の中心に近いところほど密になり、周辺部にいくほど疎になります。

さらに、人材選抜は、一回のテストで行われることが多いため、そのテスト結果は、いつ行っても、ほぼ同じ値を得るもの(同じ点数になるもの)であることが必要になります。そうでないと、運や不運に左右される不公平なテストになってしまいます。
(例えば、昨年の試験は問題が難しかったので、平均点が30点で合格者は受験者全体の10%しかいなかったが、今年は問題が易しかったので、平均点が65点で合格者は受験者全体の70%になったということでは、試験の信頼性が問われることになります。)
人材選抜における「二種類の誤り」
選抜において、横軸に「試験の成績」を、縦軸に「実際の能力」をとった上で、(横軸(「試験の成績」に)成績の合否ラインと、(縦軸「実際の能力」に)必要な能力水準の線(ライン)を引いて、四つの象限に分けると次のようになります。

象限A:試験の成績が良く実際の能力も高い層(合格するべくして合格した層)
象限B:実際の能力はあるものの(たまたま)試験成績が伴わずに不合格となった層(能力があるのに採用しそこなった層)
象限C:試験の成績が悪く実際の能力も低い層(不合格になるべくして不合格になった層)
象限D:実際の能力はないものの(たまたま)試験成績が良かったので合格となった層(能力がないのに採用してしまった層)
現実の選抜においては、「実際の能力を測ることの難しさ」や、いつ行ってもほぼ同じ結果を出すような「問題作成の難しさ」、「受験者自身の体調」や「試験自体の測定誤差」などの影響から、次のような状況が生じます。

1.実際の能力は必要な水準以上あるにもかかわらず、(運悪く)試験の成績が悪かった受験者(図ではA→Bとなるケース)
2.実際の能力は必要な水準を満たしていないものの、(運よく)試験の成績が良かった受験者(図ではC→Dとなるケース)
このように選抜を行うに際しては、できる限り「能力があるのに採用しそこなった層(象限B)」と、「能力がないのに採用してしまった層(象限D)」を少なくすることが重要になります。
このような「二種類の誤り」を少なくするために、前出の図のABCDを用いて表現すると、次のようになります。

この式は、試験によって合格したA+Dのうち、
能力、試験ともに高い受験者Aの割合(A/(A+B))から、
全受験者(A+B+C+D)のうち
実際の能力が水準以上の者の割合((A+B)/( A+B+C+D))を差し引いたものが、選抜効果(U)となることを示しています。
選抜効果に影響する各種要因分析
この選抜効果Uは、
①受験者の競争率(A+Dの大きさ)
②実際の能力が水準以上の者の割合(A+Bの大きさ)
③実際の能力と試験成績との相関係数(実際の能力と試験得点との合致度(妥当性))
によって変化することがわかっています。
①受験者の競争率(A+Dの大きさ)
図のように、全受験者の実際の能力が「求める水準以上の者」の割合は同じで、競争率(※1)のみが変化するとき、
(採用人数が絞り込まれて)競争率が高くなると合格者(A+D)に占める実際の能力が「求める水準以上の者(A)」の割合は高くなる。
他方、((例えば、採用人数を増やすことになり)合格者を増やすと)競争率が低くなると、それに伴い、合格者(A+D)に占める実際の能力が「求める水準以上の者(A)」の割合は低くなる(※2)。

(※1)合格者数を絞り込み、少なくすると、結果的に競争率は高くなり、合格者数を多く出すと、競争率は低くなります。
(※2)受験者の人数は変化しないと仮定しているので、図の楕円(網掛け部分)の面積含まれる度数も同じになります。
②実際の能力が水準以上の者の割合(求める能力水準)(A+Bの大きさ)
図のように、採用人数は変わらすに、選抜する側の「求める能力の水準」が高くなると、(採用人数=合格者数は変わらないため)合格者(A+D)に占める実際の能力が「求める水準以上の者(A)」の割合は低くなる。
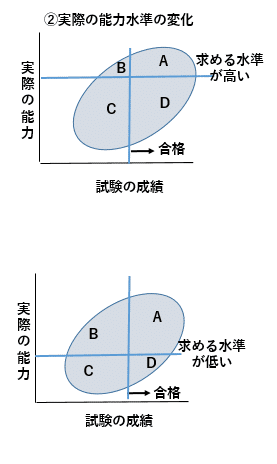
他方、(例えば、誰でもできる簡単な業務を担当する者を採用することになり)「求める能力の水準」が低くなると、(合格者数は変わらなくても)合格者(A+D)に占める実際の能力が「求める水準以上の者(A)」の割合は高くなる。
③実際の能力と試験成績との相関係数(実際の能力と試験得点との合致度(妥当性))
図のように、受験者の競争率と、全受験者の実際の能力が「求める水準以上の者」の割合が同じであるとき、「実際の能力と試験の成績との相関係数(妥当性)」が高いほど、合格者(A+D)に占める実際の能力が「求める水準以上の者(A)」の割合は高くなる※。

※受験者の人数は変化しないと仮定しているので、図の楕円(網掛け部分)の形は相関係数の違いにより異なりますが、楕円内に含まれる度数(受験者数)は同じになります。
これらのことから、
①実際の能力と試験成績との相関係数(妥当性)が高いほど選抜テストの選抜効果は高くなりますが、妥当性が低くても、受験者の競争率が高ければ、選抜効果が高まること、
また、
②一定程度の競争倍率が確保されていたとしても、選抜側が求める能力水準が高くなると、(A+Bの人数が絞り込まれ、その面積が小さくなるため)「求める能力水準を満たす者」を選ぶことが難しくなること
などがわかります。
まとめ
このように、受験者の「実際の能力」と「試験成績」との関係について、考察してきました。
人材選抜を行う私たちは、『「能力があるのに採用しそこなった層」と「能力が無いのに採用してしまった層」をいかに少なくするか』という課題を、常に考えつつ、人材選抜を行っていく必要があるのです。
また、「実際の能力」と「試験成績」との関係については、
①受験者の競争率、
②(全受験者に占める)実際の能力が水準以上の者の割合、
③実際の能力と試験成績との相関係数
の三つの要因が関係していることも分かりました。
「実際の能力」と「試験の成績」との相関係数に関しては、Ghiselli※が、数多くの適性検査について、テスト成績と職務成績との相関研究を行った結果、その多くが0.2~0.4前後であり、0.6を超えるものは知能と訓練成績のように特殊な場合に限られていると報告しています。
※Ghiselli,E.E,The validity of occupational aptitude teste,John Wiley,1966,
ワンランク上の人材選抜を私たちは、「実際の能力」と「試験の成績」との相関係数が、このように高くはないことを踏まえた上で、慎重な選抜を進めていくことが求められているのです。
今回も最後までお読みいただきありがとうございました。
次回は、人材選抜におけるジレンマの第3回目として、「採用選抜の効果とジレンマ」について、先行研究を参考にしつつ深めていきたいと思います。(Mr.モグ)
